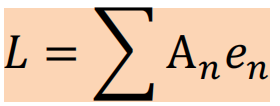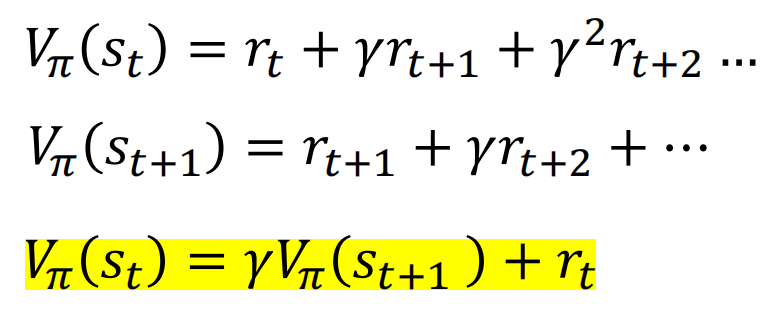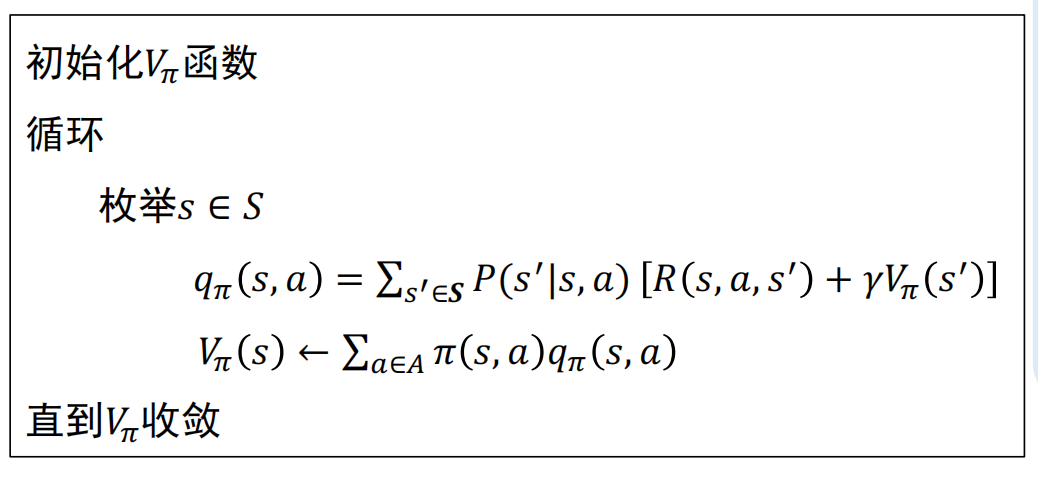AI导论-2024春-总笔记
这是北航2024春《人工智能导论》课的理论笔记,由笔者整理。
绪论
三种主流方法:符号主义、联结主义、行为主义
机器学习
从数据中学习知识:f(x)=y
按数据标注情况分类: * 监督学习:数据有标签、直接反馈、预测结果 * 无监督学习:数据无标签、无反馈、寻找数据规律 * 半监督学习:部分数据有标签,部分反馈,预测结果 * 强化学习:稀疏标签(奖励),稀疏反馈,适合做序列决策
监督学习
基本概念:从标注数据学习输入到输出的潜在关系,即函数映射
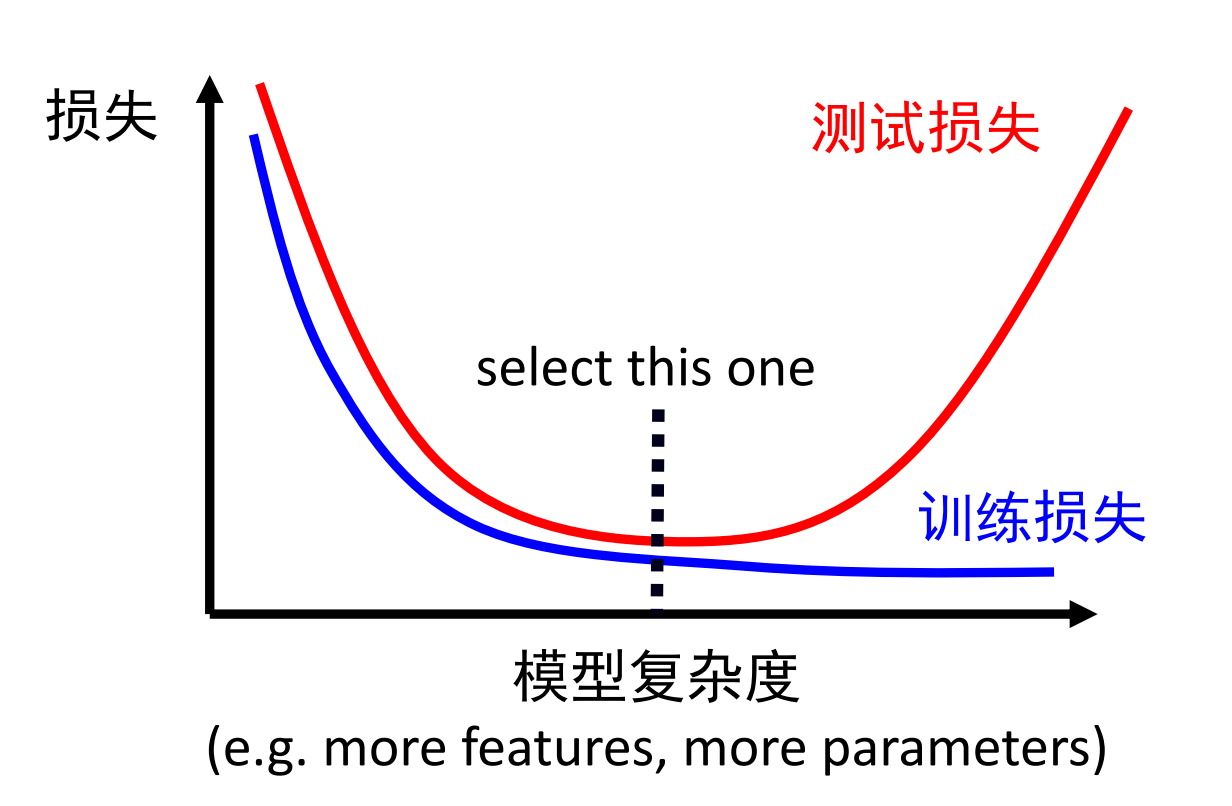
经验风险:训练集上损失函数值;期望风险:测试集上损失函数值
过拟合:经验风险小,期望风险大;欠拟合:经验风险大,期望风险大
过拟合的可能因素:数据过少;模型过于复杂
缓解过拟合:1.减小模型复杂度:正则化;减少深度学习模型层数;2.增加数据:数据增广
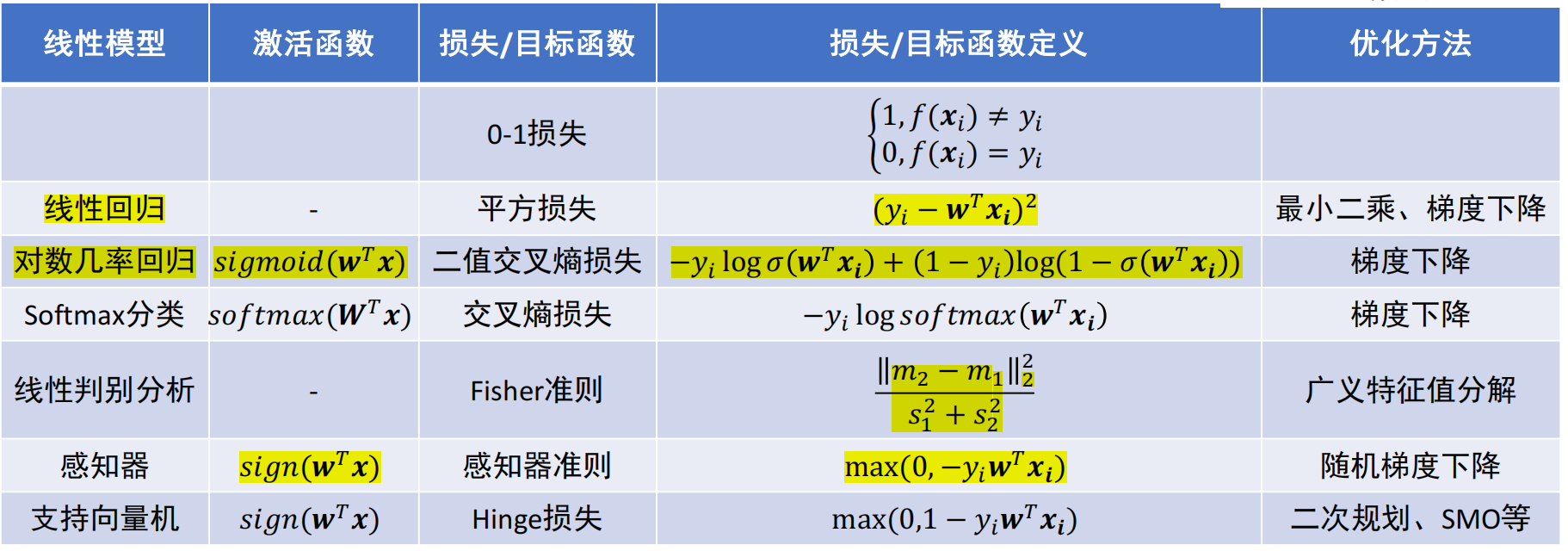
线性回归/分类
- 回归:函数输出标量(连续);分类:给定选项(类别),函数输出其中一个正确选项(离散)
- 对数机率回归:sigmoid激活函数,将回归模型转为线性分类模型;softmax函数将二分类拓展至多分类
一元线性回归
- 学习模型:
f(xi)=w·xi+b - 损失函数:
L(b,w)=sum(i=1~n)[yi-(w·xi+b)^2]. - 优化方法:最小二乘法,
L(b,w)对b,w分别求偏导,设为0
多元线性回归
对数机率回归(Logistic Regression)

从二分类到多分类:softmax
线性判别分析、支持向量机
Fisher线性判别分析
- 针对:二分类问题
- 基于监督学习的分类/降维:对一组具有标签信息的高维数据样本,将其线性投影到一个低维空 间上
- 目标:类内方差小,类间方差大
- 目标函数最大化:f(w)=||m1-m2||2/(s12+s2^2)
- 步骤:
- 1.计算数据样本集中每个类别样本的均值;
- 2.计算类间散度矩阵
Sb,类内散度矩阵Sw; - 3.求前r个最大特征值对应的特征向量(w1,...,wr),构成矩阵W
- 4.通过矩阵W,将每个样本映射至低维空间。
感知器模型
支持向量机
- 目标:最大化分类间隔(支持向量:与超平面距离最小的点)
- 求解目标函数:拉格朗日乘子法
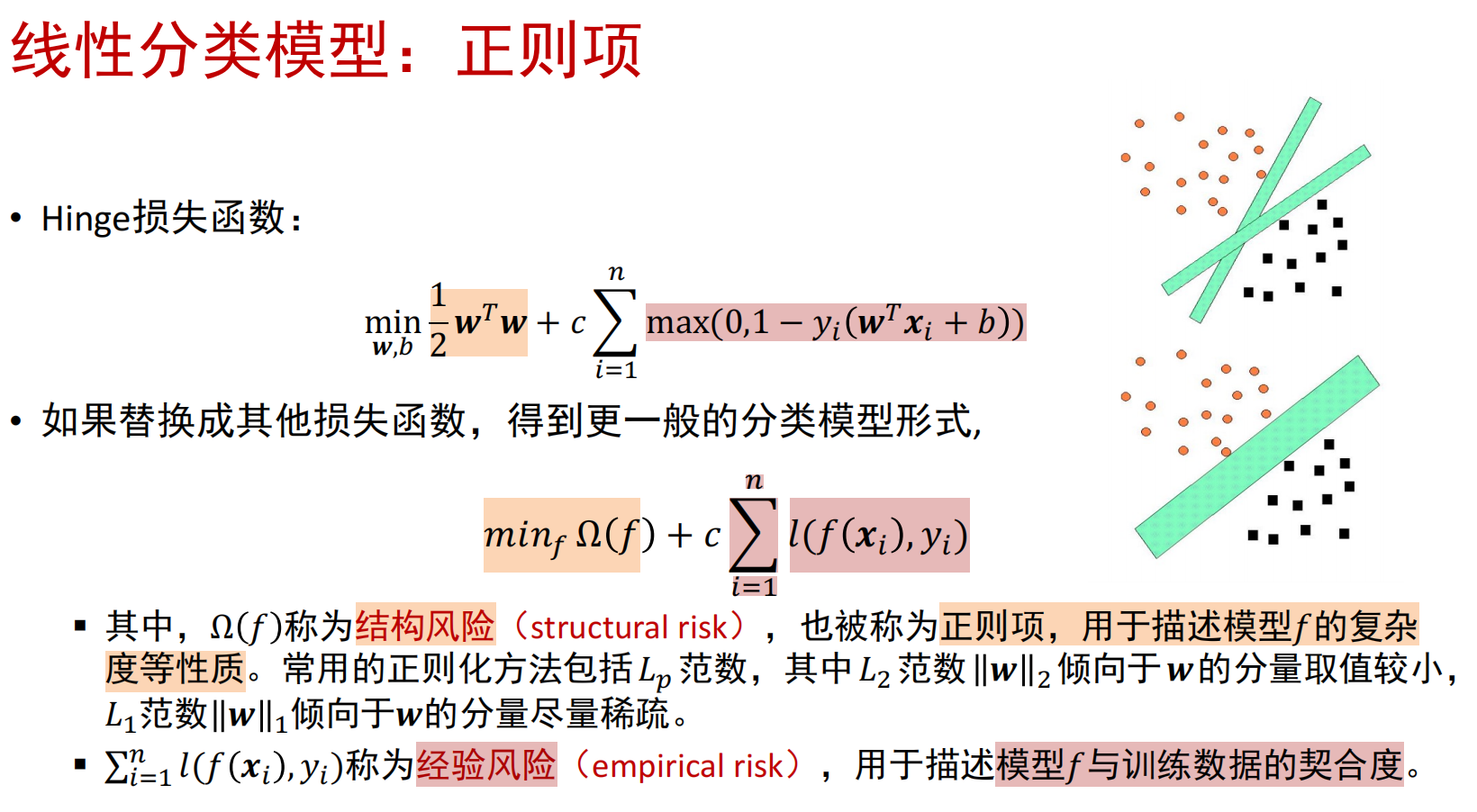
正则项
- 线性不可分-松弛变量,软间隔与hinge损失函数
决策树
信息论概念
经验信息熵:H(Y)
条件熵:H(Y|a)
已知随机变量a的条件下,随机变量Y的不确定性
划分度量
信息增益(IG)
IG(D,a)=H(Y)-H(Y|a),划分前后信息熵的差值- 选择IG值最大的属性
信息增益率(Gain_ratio)
基尼系数
- 基本思想:自顶向下递归,以信息熵为度量,构建一颗熵值下降最快的树,到叶节点处信息熵为0
- 算法流程:
- 1.训练:从空决策树开始,选择下一个最佳属性进行划分
- 2.测试
- 停止条件:
- 1.当前节点所含样本,均属同一类别;
- 2.当前属性集为空;
- 3.当前节点所含样本集合为空
剪枝
- 划分准则影响决策树的尺寸,但对泛化能力影响有限
- 解决分支过多,模型过拟合:剪枝
Ada Boosting
- 思想:将多个弱分类器组合形成一个强分类器
- 核心问题:
- 1.改变训练数据权重:提高上一轮中分类错误样本的权重;
- 2.改变弱分类器权重:提高分类误差小的弱分类器权重
- 算法流程:
- 1.初始化训练样本的权重:每个样本具有相同权重;
- 2.训练弱分类器:样本分类错误,该样本权重升高;反之降低。更新过的样本集,训练下一个分类器。
- 3.将所有弱分类器组合为强分类器:加大分类误差率小的弱分类器的权重。
无监督学习
K均值聚类
- 步骤:
- 1.初始化k个聚类质心:C={c1,...,ck},采样得到。
- 2.将每个未聚类数据xi,分别放入:与之距离最近聚类质心所在聚类集合:argmin d(xi,cj)
- 3.更新聚类集合的质心位置;
- 4.重复步骤2,3.
- 5.终止条件:达到迭代次数上限;或者,多次迭代后,聚类质心基本不变。
- 目标函数:
最小化每个类簇的方差。
- 性质:
- 1.目标函数严格单调递减;
- 2.目标函数在有限步内收敛。
- 不足:
- 1.需要事先确定聚类数目;
- 2.初始化的聚类质心影响结果;
- 3.欧式距离假设数据的各维度重要性相同。
主成分分析
- 思想:降维,原始数据投影至一个新的坐标系,使得:投影后数据方差最大
- 目标函数:如何寻找映射矩阵W,使得:
- 角度1:投影后数据方差最大;
- 角度2:重构误差最小
- 角度1:投影后数据方差最大;
- 步骤:
- 1.数据预处理:X=(X-μ)/σ.
- 2.计算协方差矩阵:R=[X(T)X]/n-1. R是mxm维矩阵
- 3.求矩阵R的特征向量和特征根;
- 4.取前l个最大的特征根对应特征向量,组成映射矩阵W(mxl).
- 将m维向量X,映射至l维向量Y:Y(1xl)=X(1xm)·W(mxl).
- X(1xm)=Y(1xl)(W(T))(lxm).
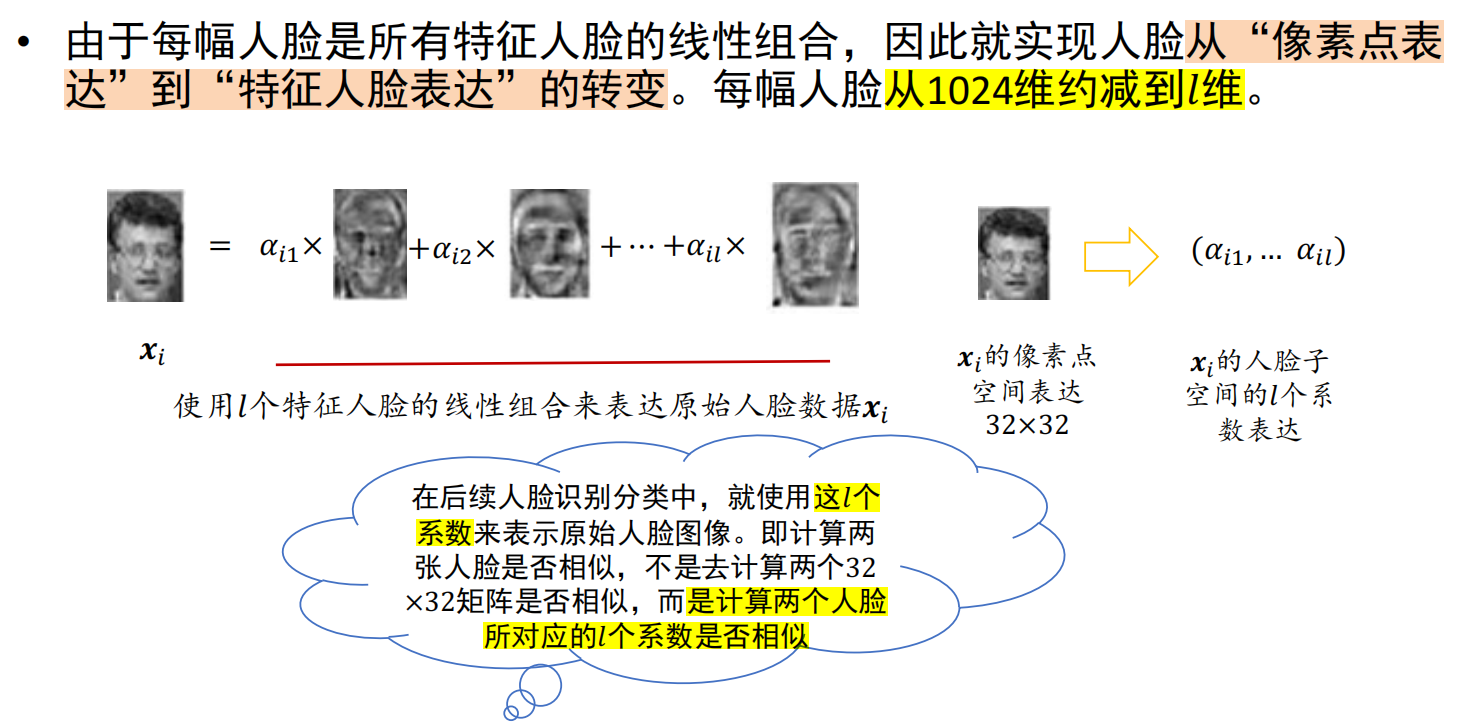
基于特征人脸的降维
n个1024维人脸样本数据,降维至l维 * 定义: - 人脸样本数据:32x32图像->1024x1列向量 - l个特征人脸:映射矩阵W(1024x1024):每个特征向量均为1024x1的列向量,可还原成32x32的人脸图像,因此称为:特征人脸。 - 人脸的新表达:
局部线性嵌入(LLE)
- 步骤:
- 1.确定邻域大小:类似KNN算法,找到某个样本的k个最近邻;
- 2.确定目标损失函数:求解线性关系的权重系数W
- 3.利用权重系数W,在低维里重构样本数据。
即:
深度学习
与机器学习区别:模型更复杂;能够自动学习特征表示;激活函数非线性
线性回归和梯度下降
- 训练步骤:
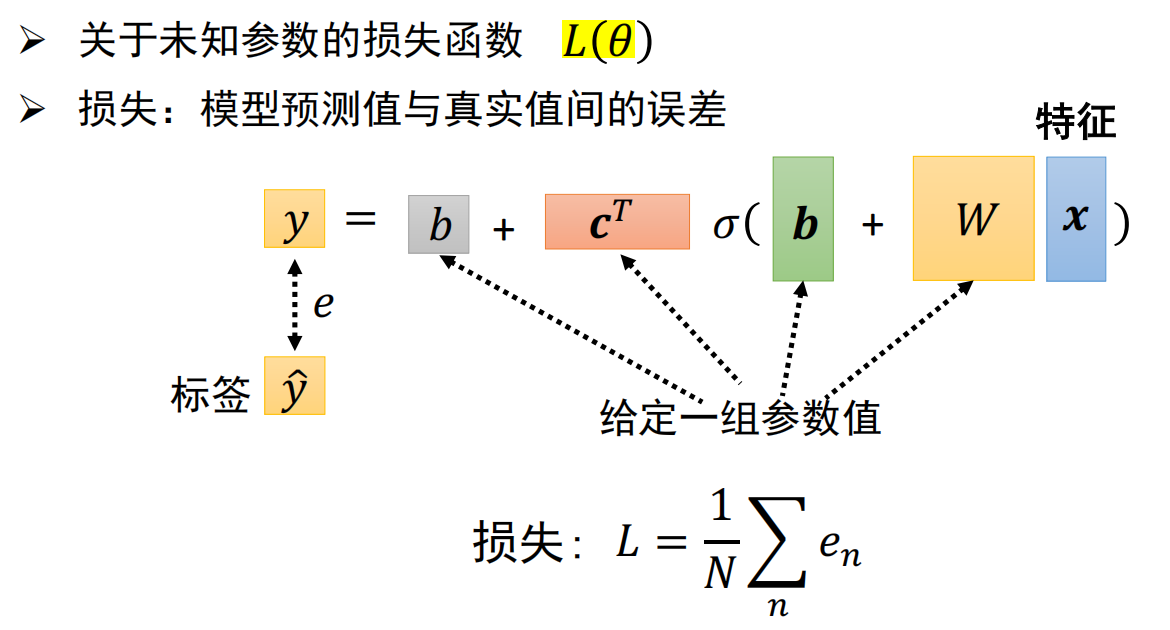
- 1.定义带有未知参数的函数:y=b+w·x.(w,b是未知参数)
- 2.定义损失函数:MAE,MSE,交叉熵损失等
- 3.优化:梯度下降
损失函数L分别关于参数w和b求偏导;迭代更新w和b
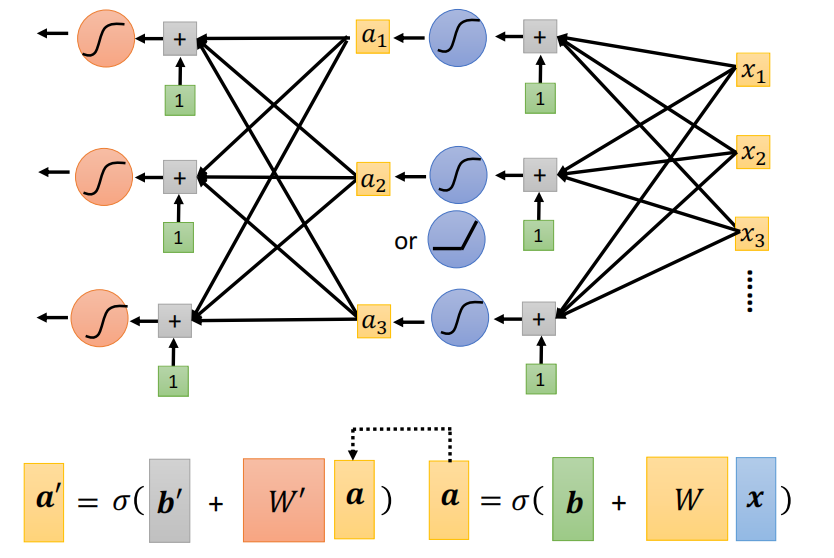
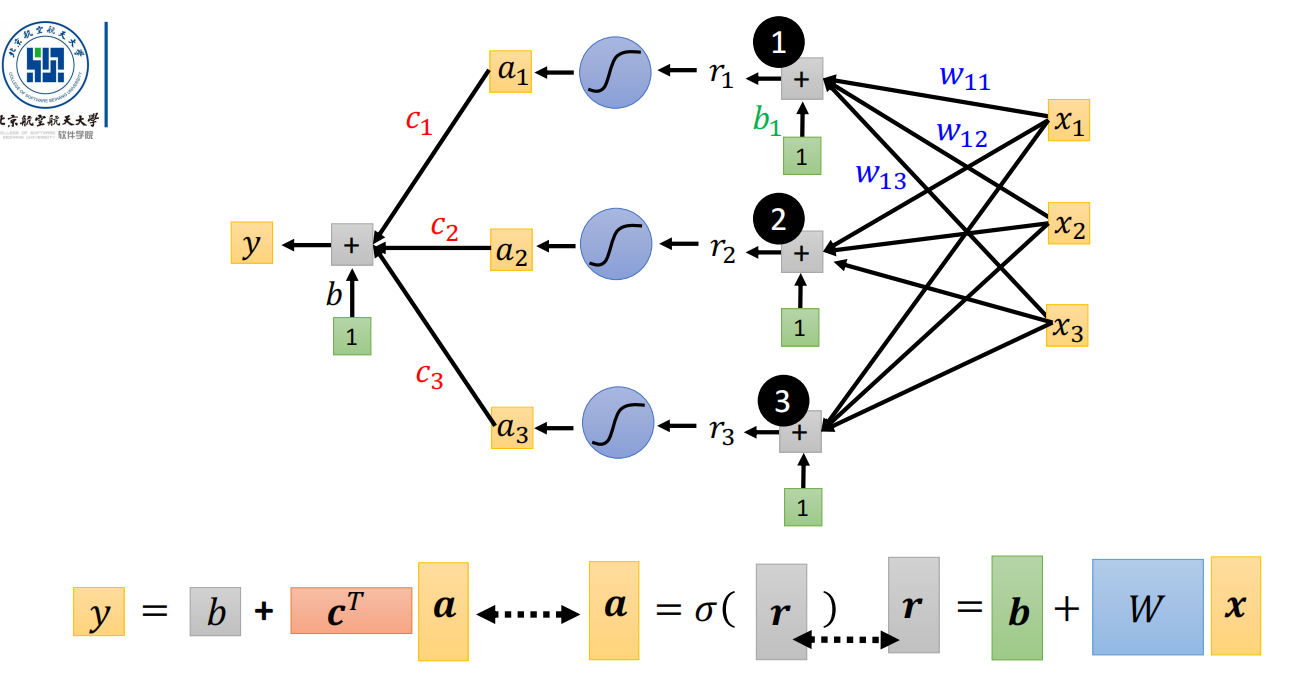
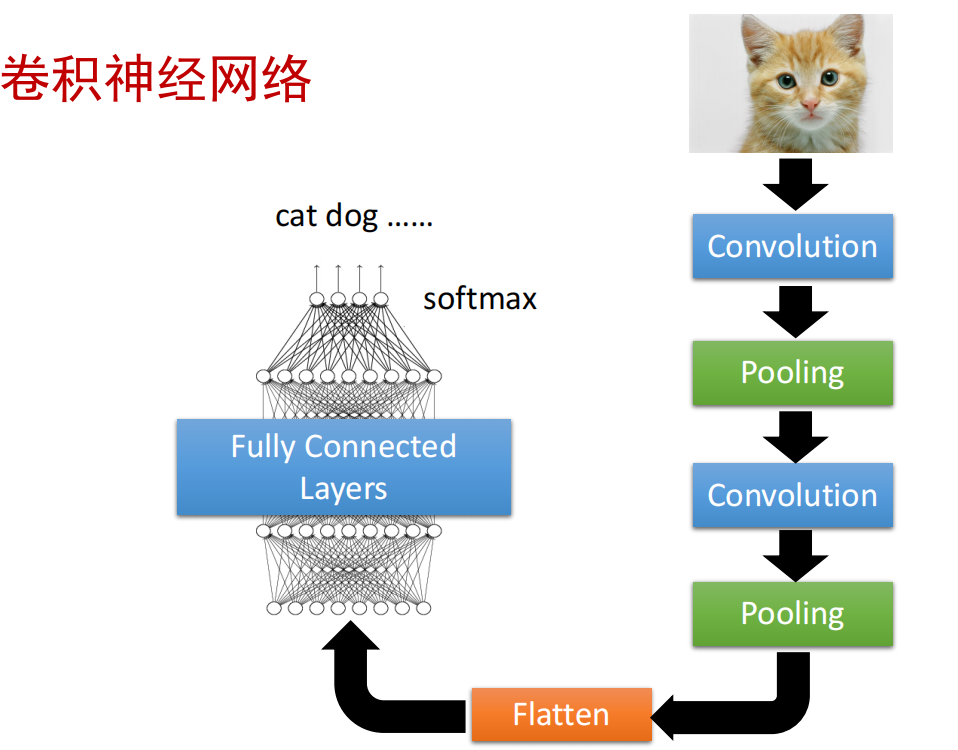
前馈神经网络/全连接网络/多层感知机
- 性质:
- 输入层、输出层和至少一层的隐藏层构成;
- 各个神经元接受前一级的输入,并输出到下一级,模型中没有反馈;
- 两个相邻层之间的神经元完全成对连接;但层内的神经元不相互连接。
- 注意:参数不能初始化为相同的值
- 如果参数被初始化为相同的值:在误差反向传播过程中,同一层的神经元所接收到的误差都相同,更新后这些参数的值仍然相同。
- 不管经过多少轮迭代,同一层神经元的参数保持相同,因此不同的神经元无法学习到不同特征的重要程度。
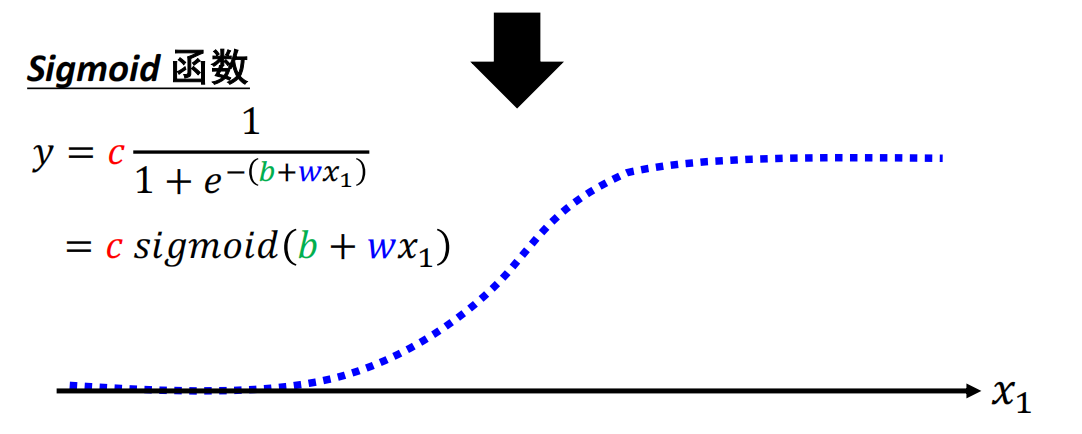
激活函数
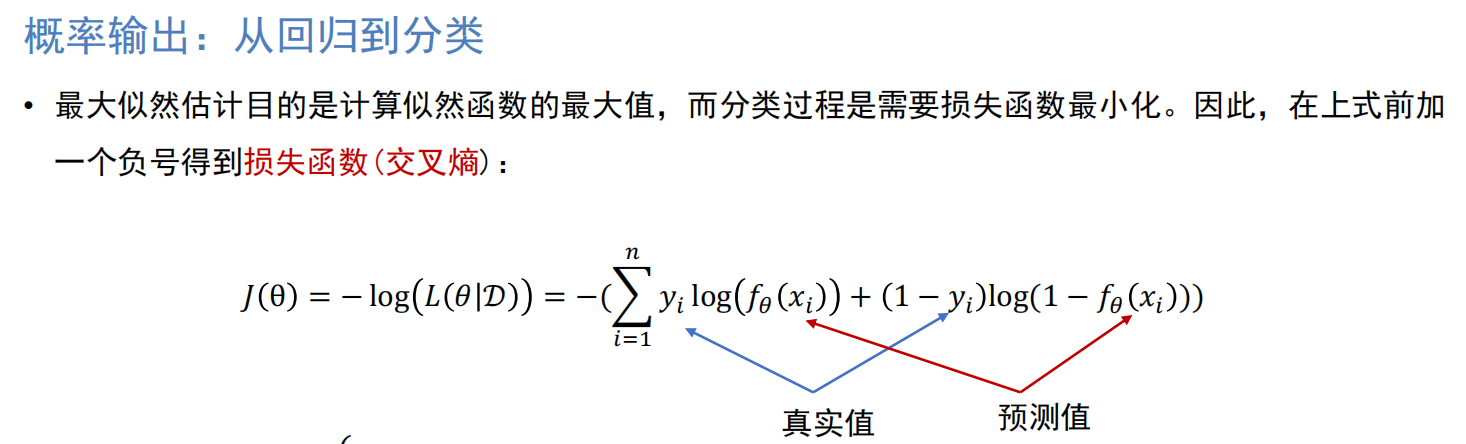
sigmoid函数
激活函数:sigmoid函数
损失函数:
优化:
sigmoid作为激活函数的不足:
- 1.饱和点附近:梯度趋于0,经过链式法则后易使梯度流消失,零梯度传至下游的节点。
- 2.参数更新方向受限,更新效率较低。
ReLU函数
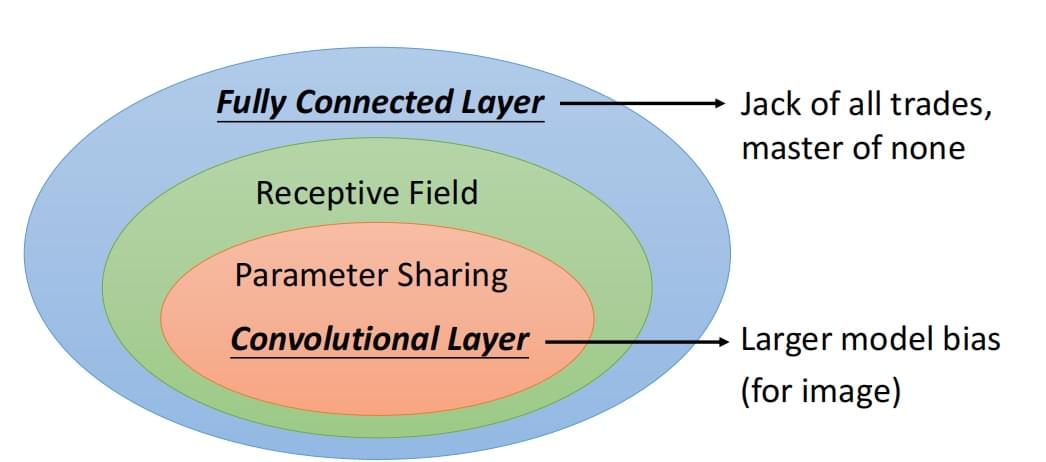
卷积神经网络
- 全连接网络参数量:W,b 例:假设输入图像大小为3 x 100 x 100,分类类别数为1000个, 如果用一层全连接网络实现分类,需要多少参数? 输入特征数量:3 x 100 x 100 输出特征数量:1000 全连接层:每个输入特征都会连接到每个输出特征;每个输出特征一个偏置项; 共30000 * 1000 + 1000 = 30,001,000个参数
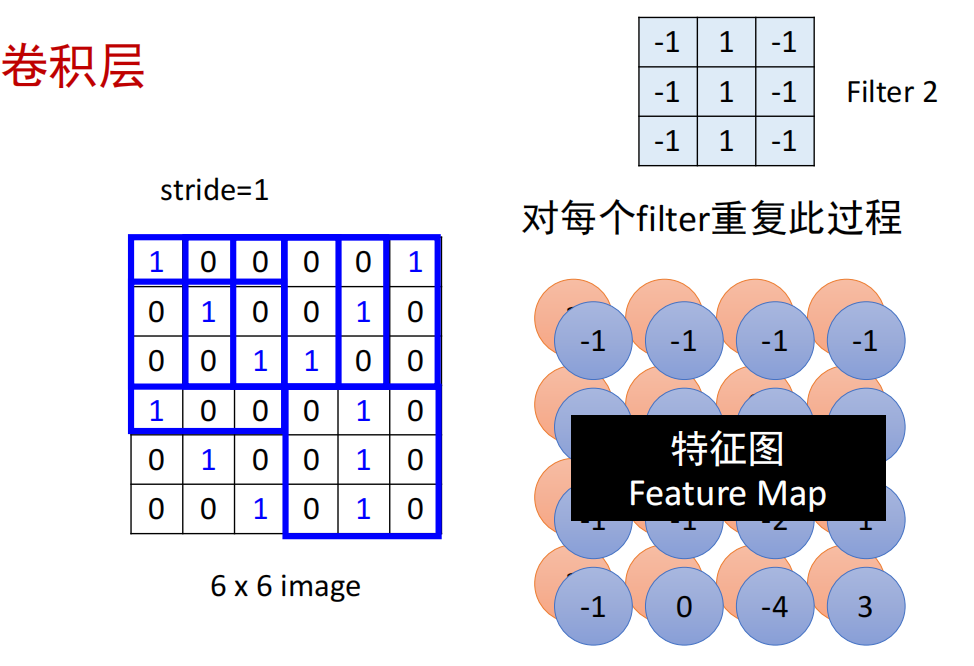
卷积层
原图像:W1 x H1 x D1,卷积核大小:F x F x D1,卷积核个数:K
零扩展:Z
步长:S
- 输出尺寸:
W2=(W1+Z*2-F)/S+1.
H2=(H1+Z*2-F)/S+1.
D2=D1.- 输出参数量:(F*F*D1+1)*K.- 步骤:每个Filter扫过整张图做卷积
- 每个感受野(Filter大小)对应一个神经元;
- 不同感受野的神经元共享参数(在不同感受野的filter相同,每个Filter扫过整张图做卷积)
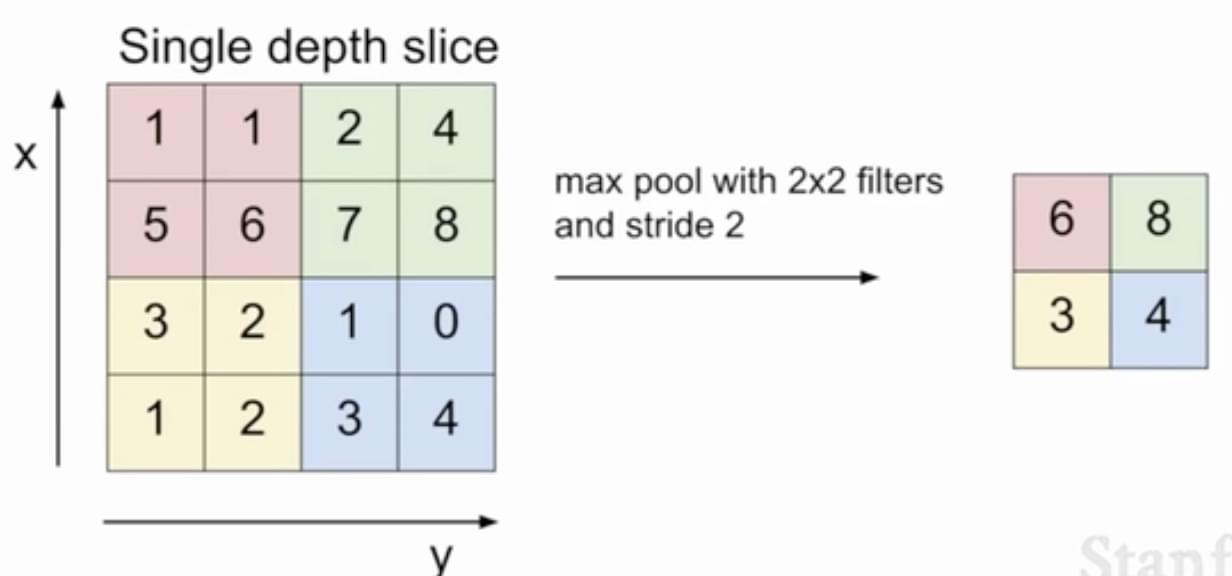
池化层
- 定义:选择该区域内的元素最大值
数据增广
- 原因:CNN中的卷积操作,不满足尺度和旋转不变性
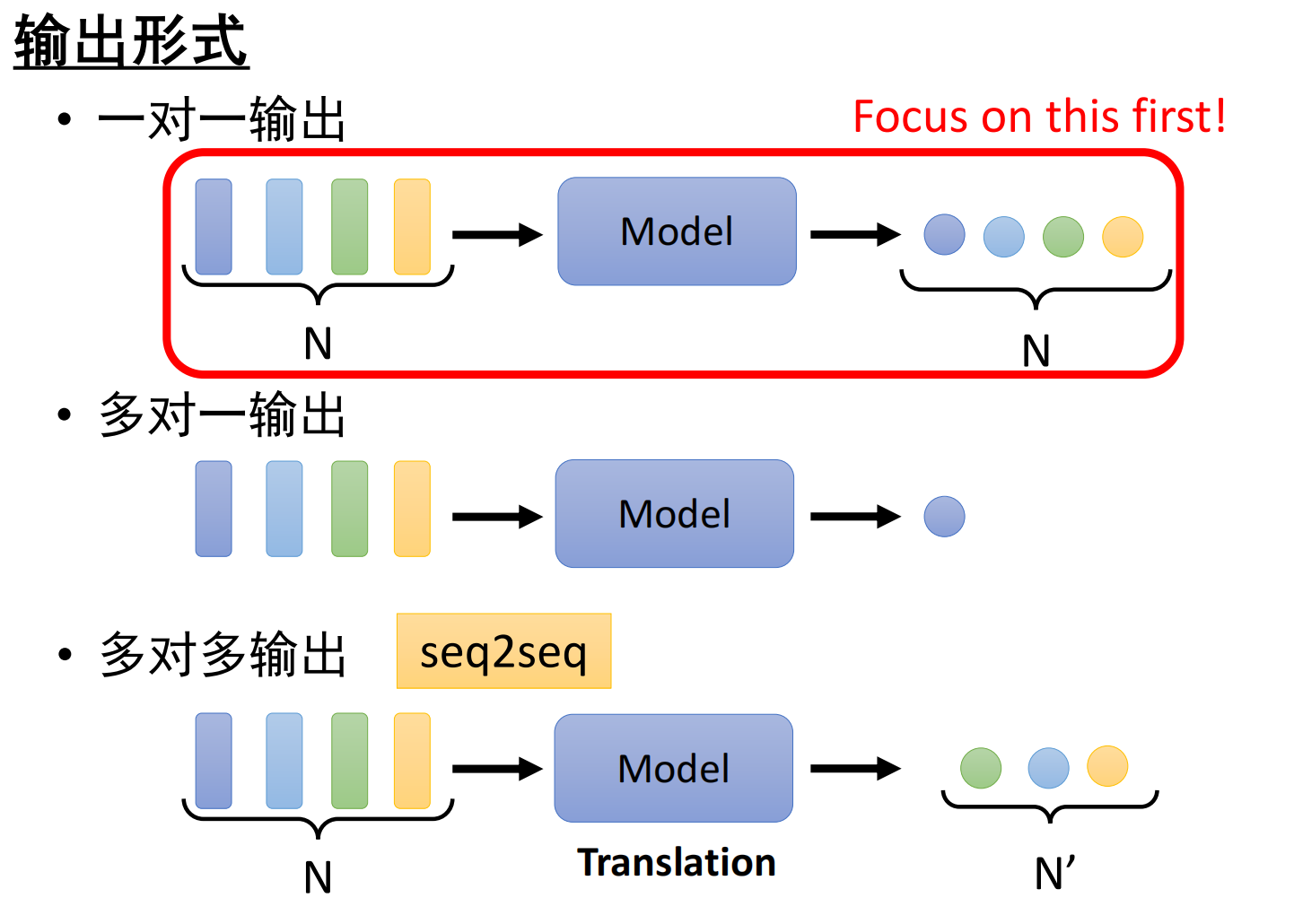
序列数据模型
- 输入形式:向量集
- 输出形式:
- 建模上下文信息:
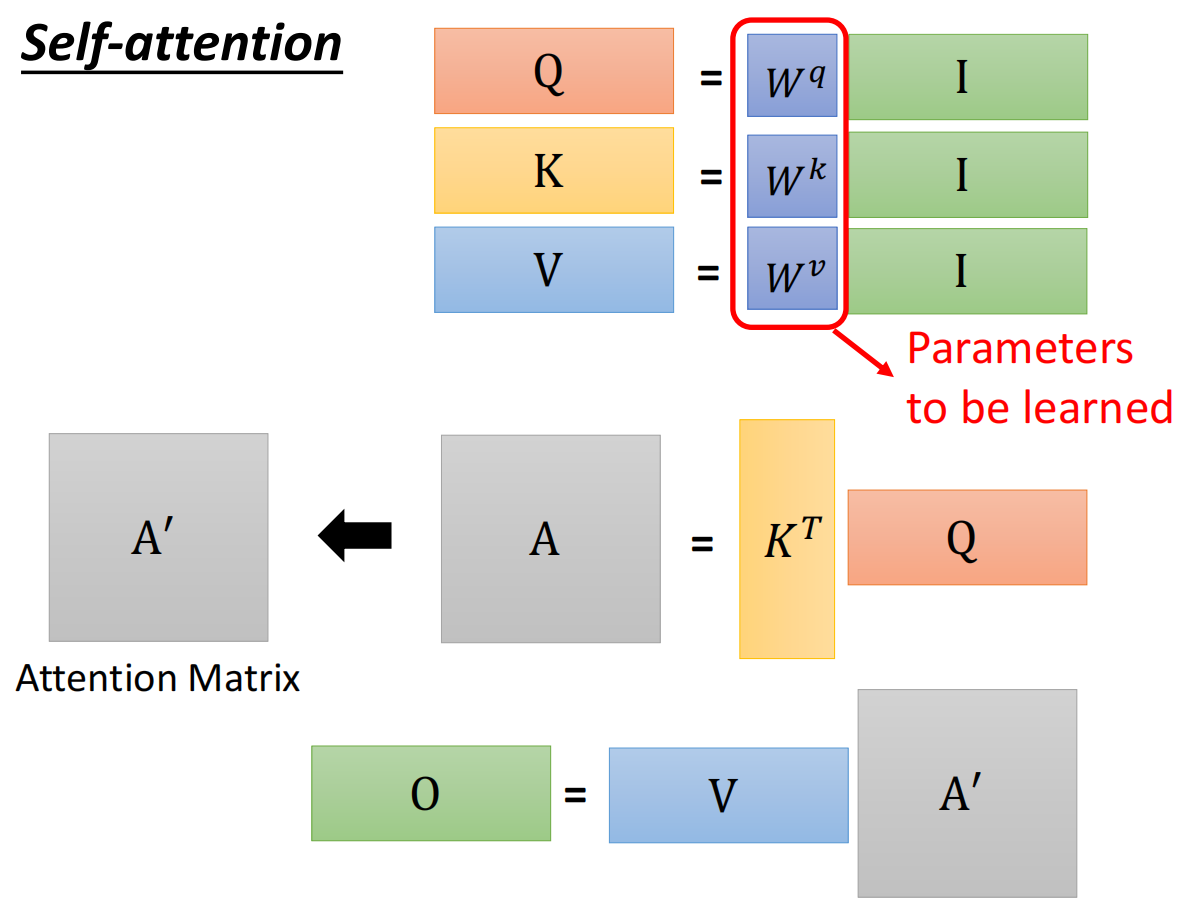
自注意力机制
- 定义:将单个序列的不同位置关联起来,以计算同一序列的表示的注意机制。
- 思想:
- Attention机制:发生在Target的元素Query和Source中的所有元素之间;
- Self-Attention机制:发生在Source内部元素之间,或者Target内部元素之间,也可以理解为Target=Source这种特殊情况下的注意力计算机制。(即Self-Attention只关注输入本身or只关注关注对象本身)
- 优点:一组元素内部相互做注意力机制,可以建立全局的依赖关系,扩大图像的感受野。相比于CNN,其感受野更大,可以获取更多上下文信息。
- 缺点:通过筛选重要信息,过滤不重要信息实现的,这就导致其有效信息的抓取能力会比CNN小一些。只有在大数据的基础上才能有效地建立准确的全局关系,而在小数据的情况下,其效果不如CNN。
- 步骤:
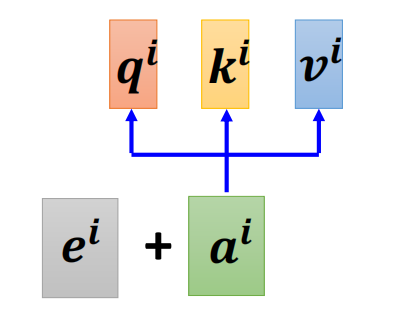
1.有矩阵Wq,Wk,Wv,对于每个输入的词向量a,分别计算其查询向量q、键向量k、值向量v。
2.计算当前单词的查询向量qi,与其它各个单词的键向量的内积;做softmanx处理,得到Score
3.用每个单词得到的score,和其值向量v的各个元素相乘,将向量相加并输出。
总过程:
引入位置编码
- 原因:self-attention中缺失了位置信息.
- 解决方案:可以给每个位置赋予一个唯一的位置编码向量(可手工设计/从数据中学习)
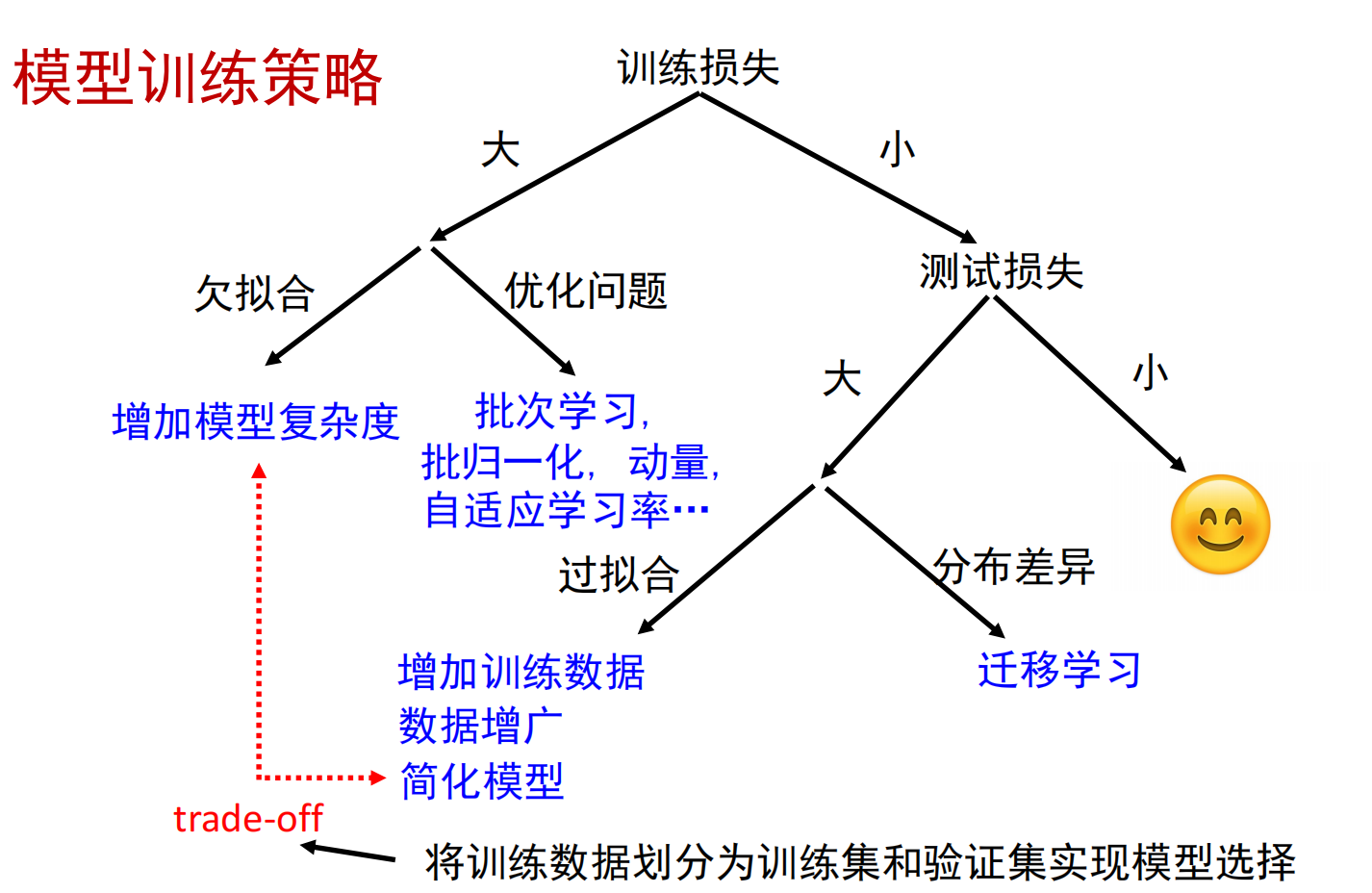
模型训练策略
- 训练损失大:区分欠拟合和优化问题
- 从易优化的浅层网络(或传统方法)开始尝试
- 如果加深网络无法得到更小的训练损失,可以认为是优化问题
- 训练损失小,测试损失大:过拟合
- 过拟合:增加模型复杂度,测试损失不降反增
- 过拟合:增加模型复杂度,测试损失不降反增
生成式模型
- 目标:数据升维
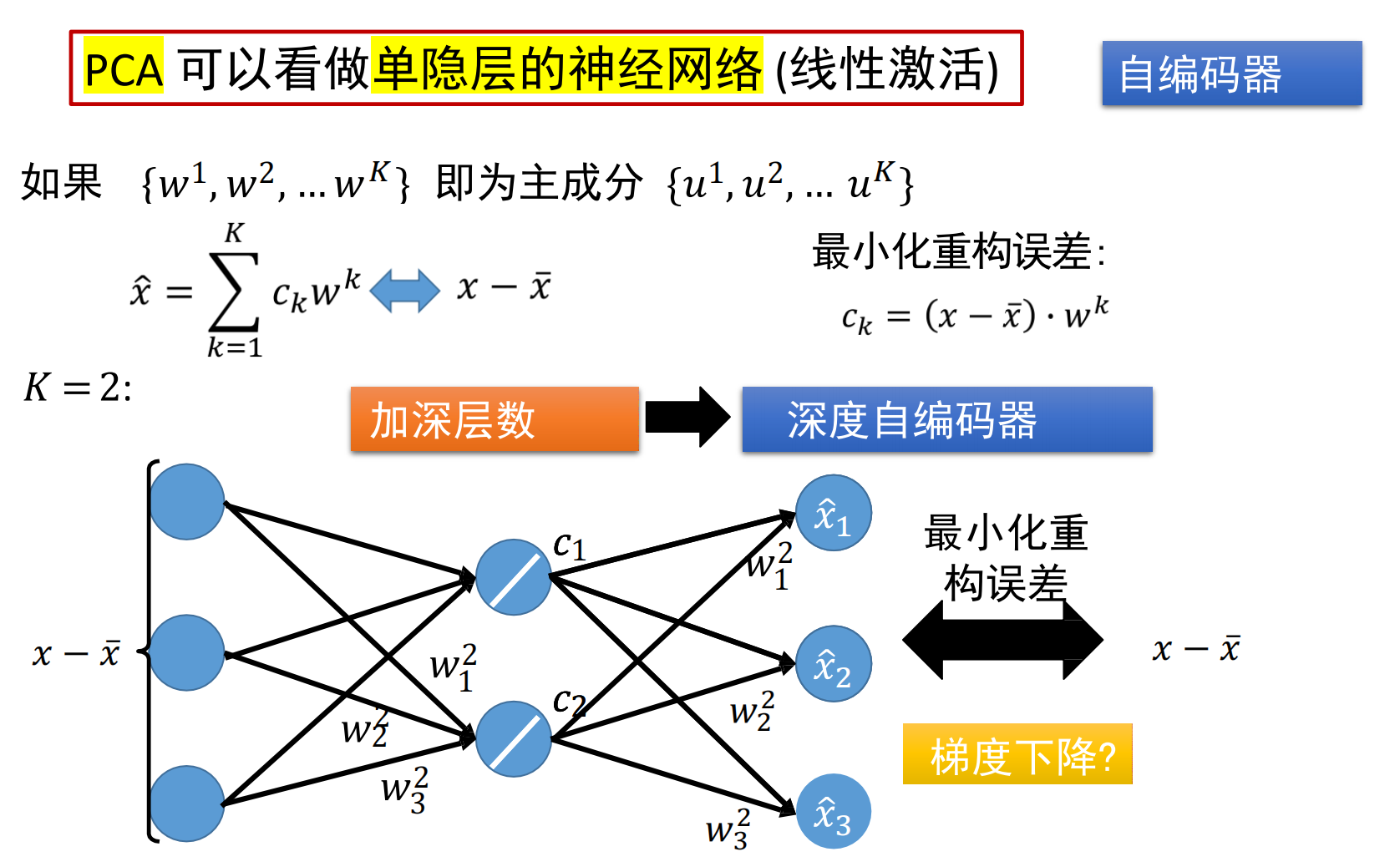
自编码器
目标:最小化重构误差
单层自编码器与PCA不一致:
- PCA有正交约束;自编码器不需要
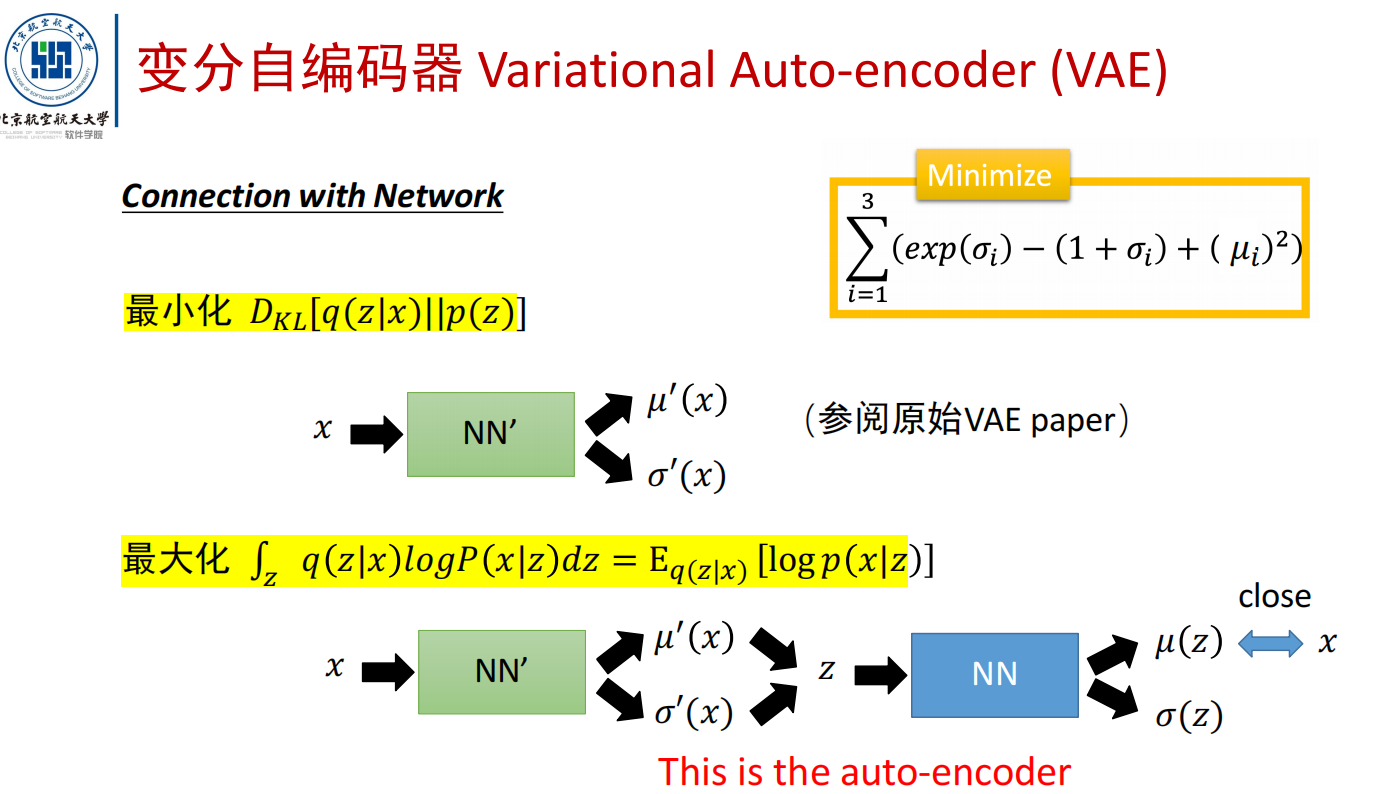
变分自编码器(VAE)
- 思想:最大化观测数据x的似然L
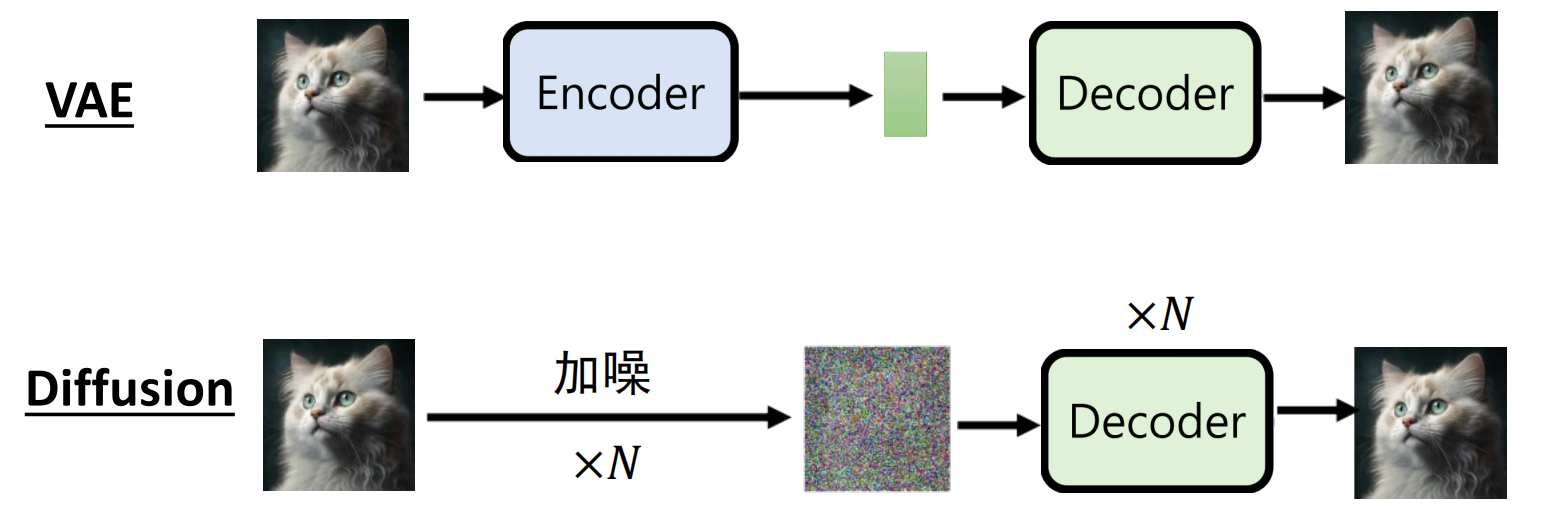
扩散模型(DDPM)
与VAE对比:
过程:
前向过程:加噪
后向过程:去噪
对抗式生成网络(GAN)
强化学习
- 特征:
- 与环境交互学习;
- 训练时间复杂度高,测试时间复杂度低;(训练难,测试易)
- 可解释性低
- 输入/输出:
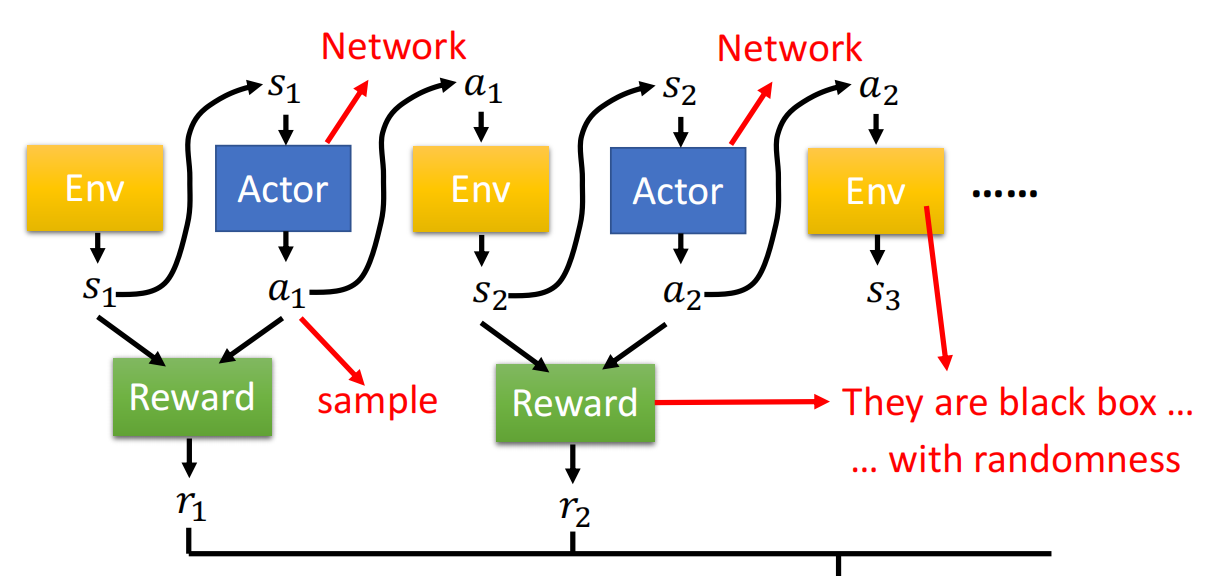
- 输入:状态(State)
- 输出:动作(actor),与环境交互,产生reward
- 四个要素:状态,动作,环境,奖励
- 适用场景:稀疏标签(奖励);稀疏反馈;序列决策
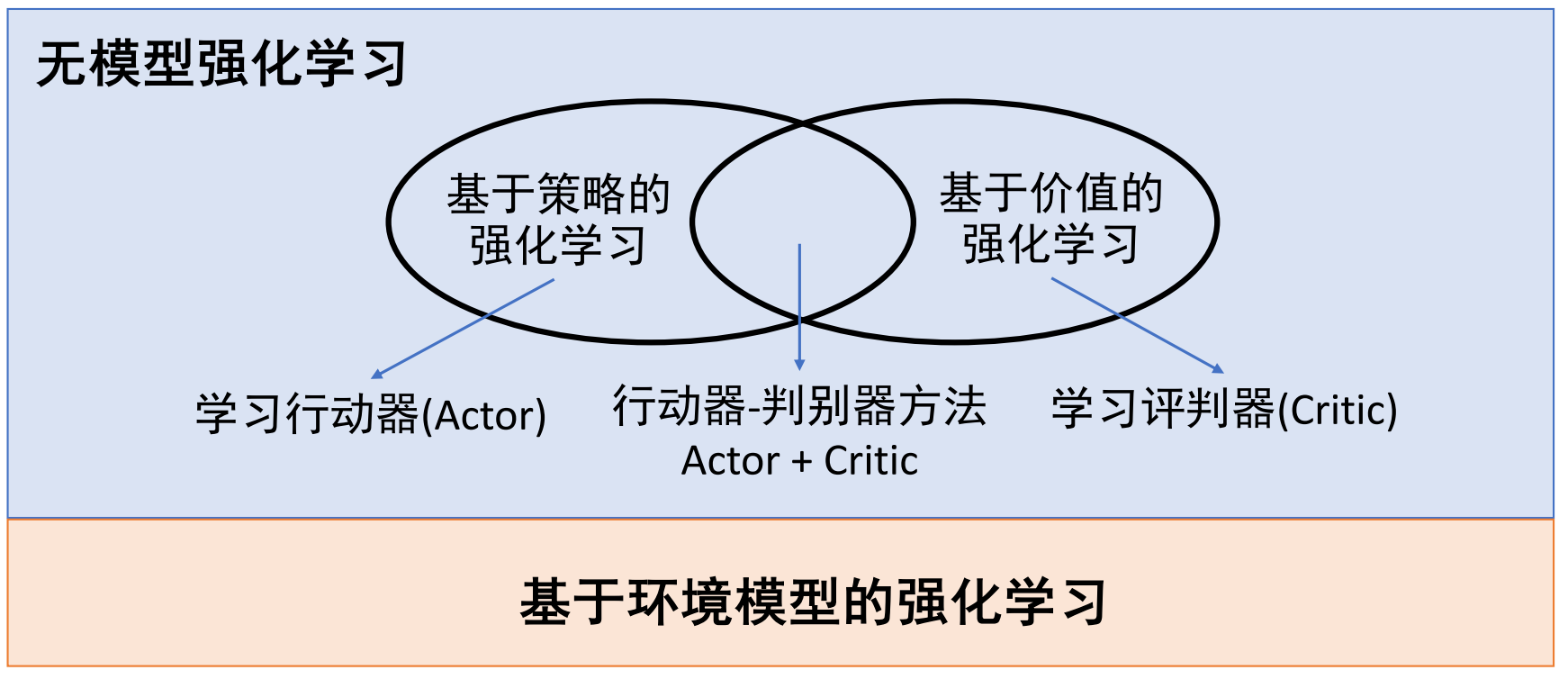
无模型强化学习
分类:
- 基于策略的强化学习(Policy-based)
- 显式学习:策略函数
- 无价值函数
- 基于价值的强化学习(Value-based)
- 显式学习:价值函数
- 隐式得到:策略(可以通过价值函数得出策略)
- 行动器-判别器方法( Actor-Critic )
- 显式学习:策略函数和价值函数
马尔可夫决策过程
通过MDP={S,A,Pr,R,γ}来刻画马尔科夫决策过程,包括:
- 随机变量序列{St},t=0,1,2,...;(状态)
- 动作集合A
- 状态转移概率Pr(S(t+1)|St,at),其中at∈A. [可以是确定/随机概率性的]
- 奖励函数:R(St,at,S(t+1))
- 衰退系数:γ∈[0,1].
策略函数
- 策略函数π:SxA->[0,1].其中π(S,A)的值表示:在状态S下采取动作A的概率
- 确定的策略:给定s的情况下,有且仅有一个动作a,使得:π(s,a)=1.
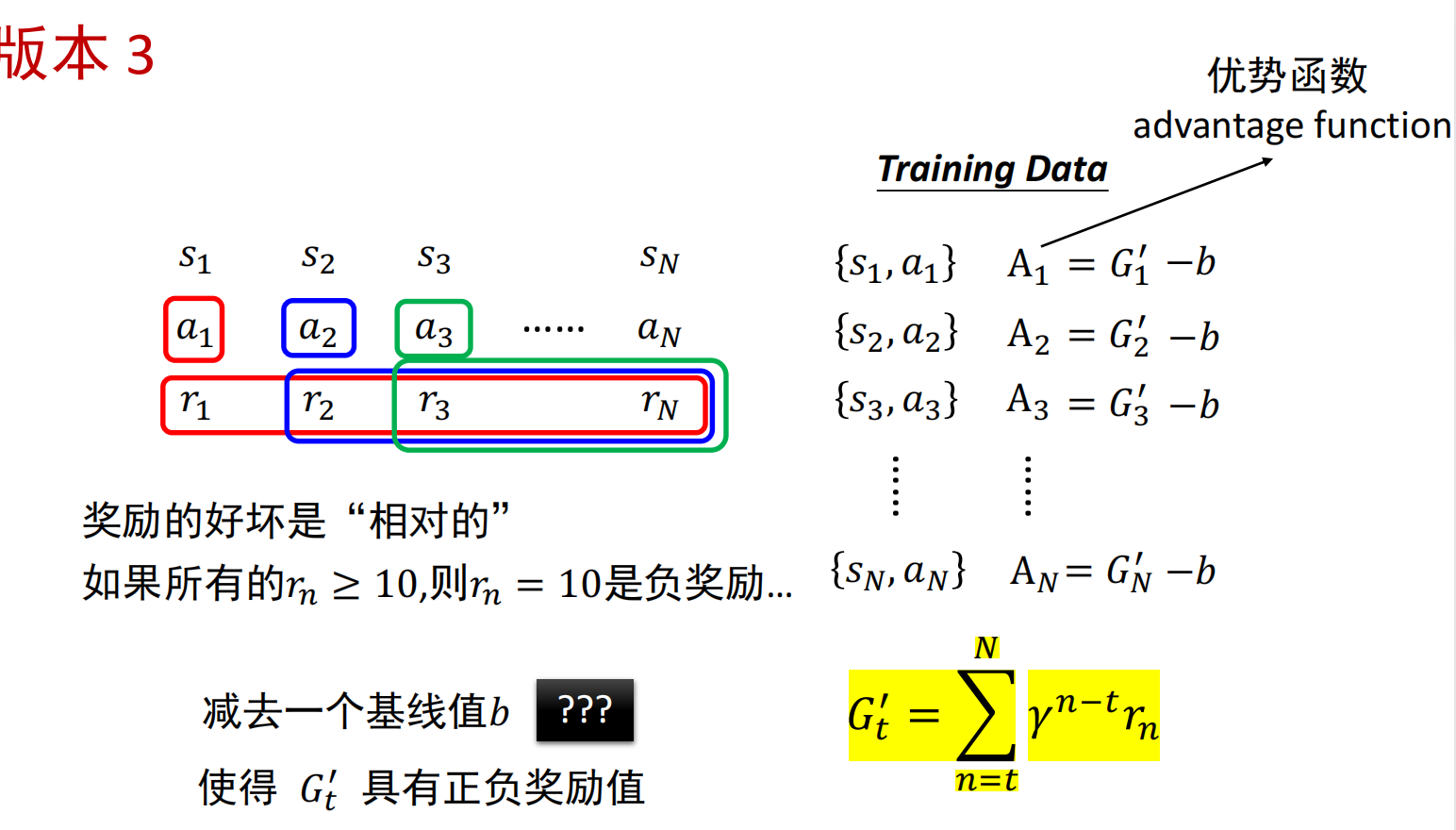
- 如何进行策略学习:一个好的策略是,在当前状态下采取了一个行动后,能在未来收到最大化的回报Return:Gt=R[t+1]+γR[t+2]+γ^2·R[t+3]+...
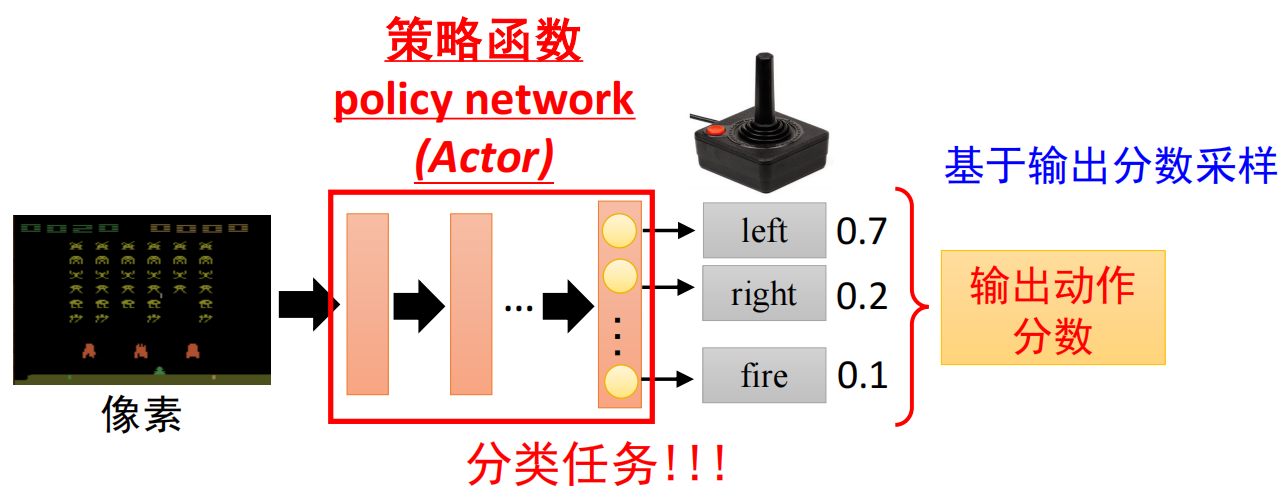
基于策略的强化学习:学习行动器(Actor)
- 步骤:
1.定义带有未知参数的函数: 输入:向量/矩阵形式的状态数据 输出:每个神经元对应的动作,基于输出分数对动作采样(具备一定的随机性)
2.定义损失函数:最大化累积奖励
3.优化:
- 策略梯度法:直接学习策略函数π
- 数据采集:在训练迭代过程的“for循环”内部完成;
- 每次模型的更新,需要重新采集整个训练数据集 损失:

基于价值的强化学习:学习评判器(Critic)
价值函数,动作-价值函数
- 价值函数:(注意与Return/Reward的区别)
- Reward奖励:R(St,at,S(t+1)),从状态St经过动作at转移至状态S(t+1)的奖励
- Return回报:Gt=R[t+1]+γR[t+2]+γ^2·R[t+3]+...
- 价值函数取值与时间无关,只与以下因素相关:策略π、在策略π下从某个状态转移到其后续状态所取得的回报、在后续所得回报有关
- 动作-价值函数:
- 动作-价值函数取值同样与时间没有关系,而是与瞬时奖励和下一步的状态和动作有关。
- 价值函数与动作-价值函数的关系
评判器
- 对于价值函数的评判器(Vπ(S)):对于策略π,评判状态s的好坏;输出值与当前策略π有关
- 对于价值-动作函数的评判器(qπ(s,a)):
贝尔曼方程:递推关系
策略优化:根据Vπ优化π

策略评估:根据π计算Vπ/qπ
动态规划法
- 方法:迭代求解贝尔曼方程组
- 局限:
- 1.要求状态转移概率已知;
- 2.无法处理状态集合大小无限的情况。
蒙特卡洛采样
大数定理指出:对于独立同分布的样本数据,当样本足够大的时候,样本平均值向期望值收敛。 思想:采样;通过样本均值估计期望 * 若为确定的策略,每个起点只有一个轨迹。
时序差分法
策略迭代
- 步骤:
- 1.策略评估:从任意策略π开始,计算该策略下的价值函数Vπ(S)或动作-价值函数qπ(s,a);
- 2.策略优化:根据价值函数Vπ(S)调整策略π;
- 迭代上述步骤,直至策略收敛。
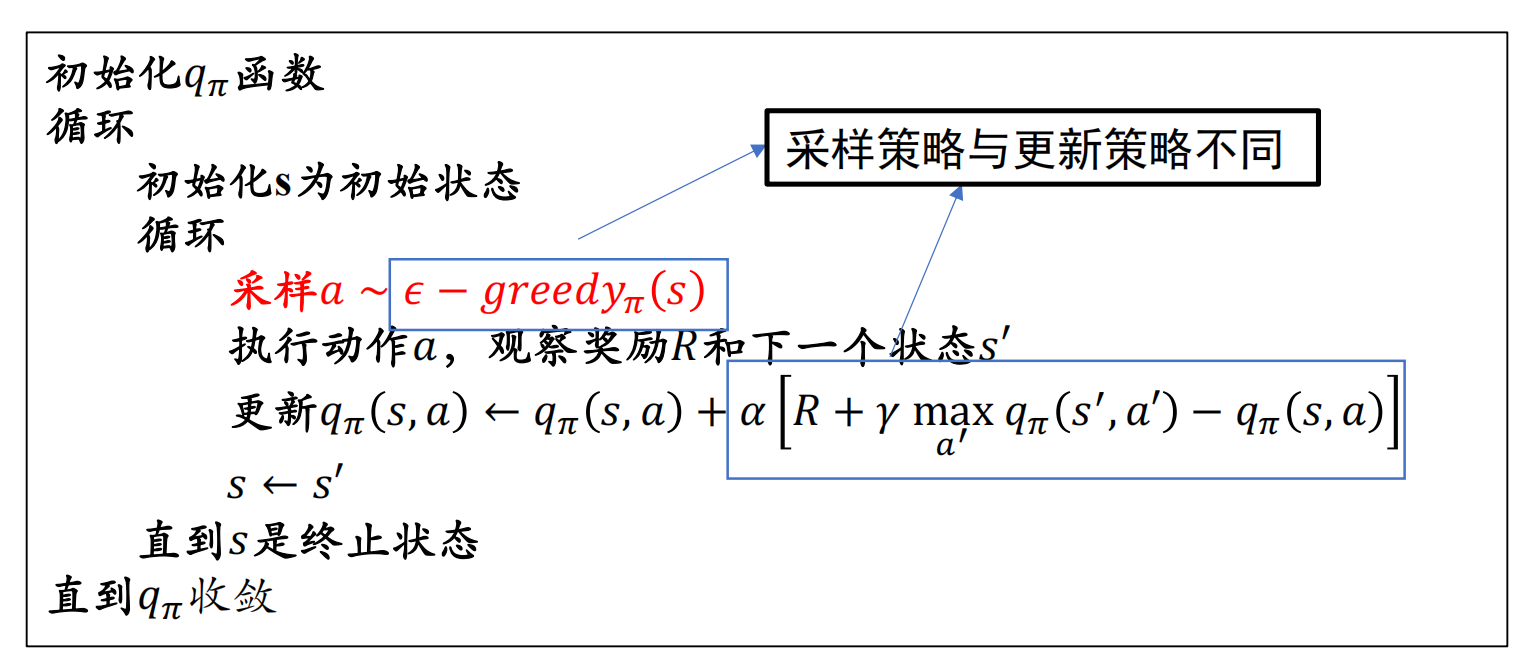
Q-learning
- 基于动作-价值函数,Q Table存储:该状态下各种动作的qπ(s,a)
- 步骤:对当前状态s,
- 1.策略优化:取动作a=argmax qπ(s,a),即状态s下的回报最大的动作a,执行a得到下一个状态s'.
- 2.策略评估:时序差分思想,更新qπ(s,a)
- 3.移至下一个状态s'(s'为终止状态时结束)
- ε贪心策略:在状态s,采样动作a时: 以1-ε的概率选择带来最大回报的动作,以ε的概率随机选择一个动作。
- 目标:达成探索和利用的平衡
- 目标:达成探索和利用的平衡
Deep Q-learning(DQN)
- 原因:状态太多时,部分状态难以采样到
- 思想:用神经网络拟合










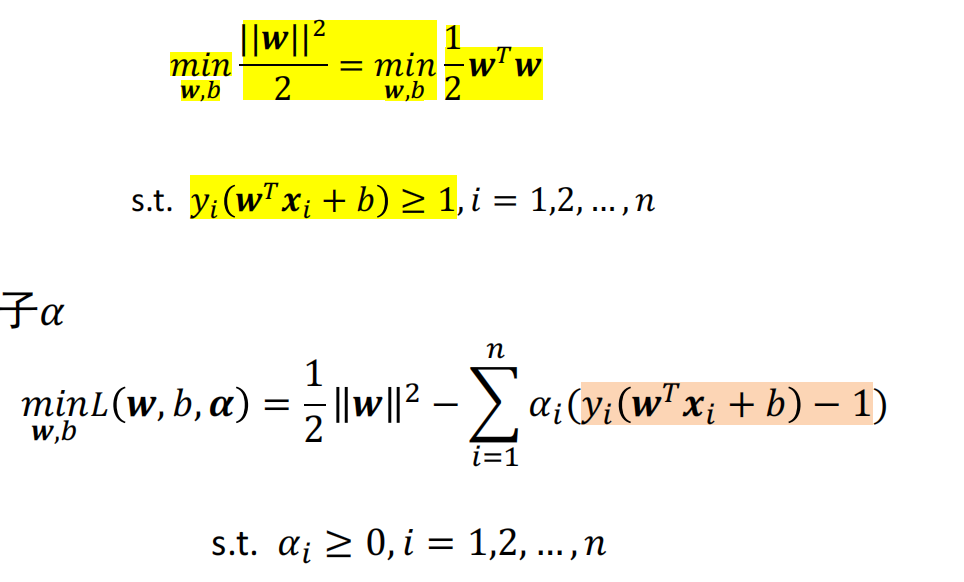
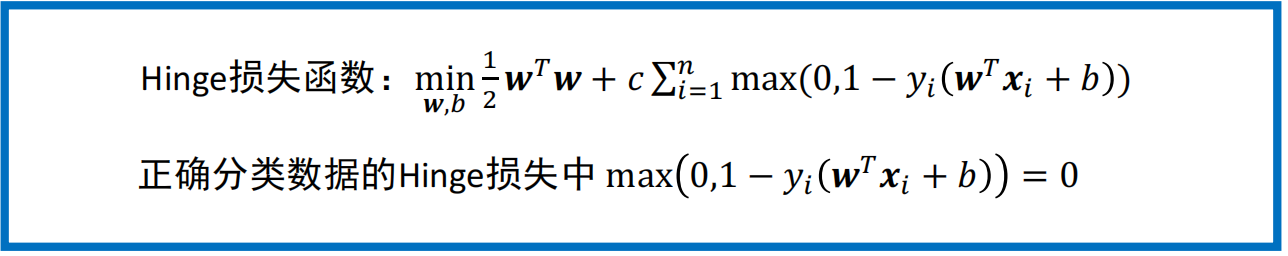


 最小化每个类簇的方差。
最小化每个类簇的方差。



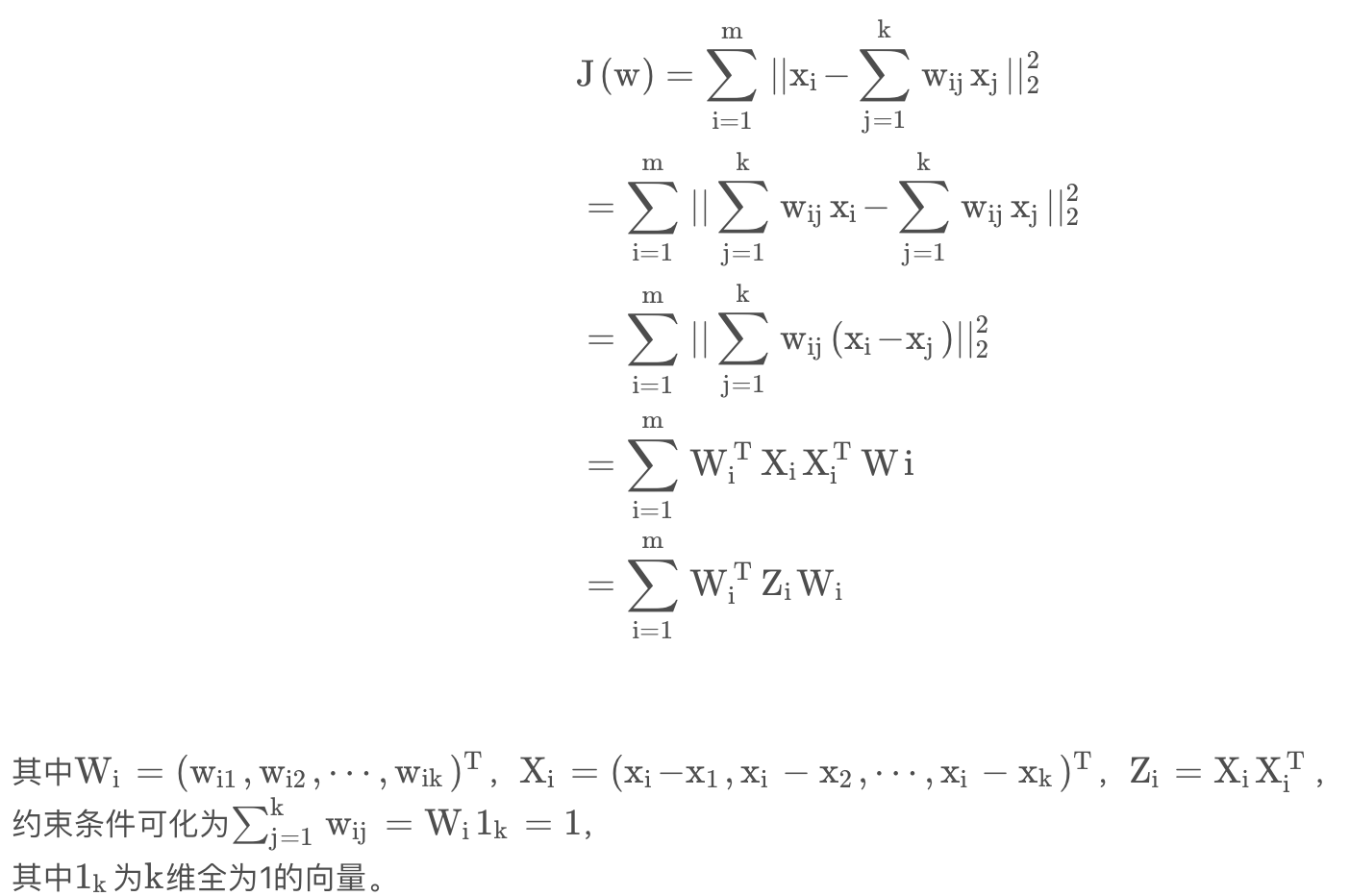




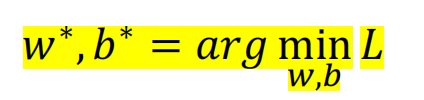 损失函数L分别关于参数w和b求偏导;迭代更新w和b
损失函数L分别关于参数w和b求偏导;迭代更新w和b 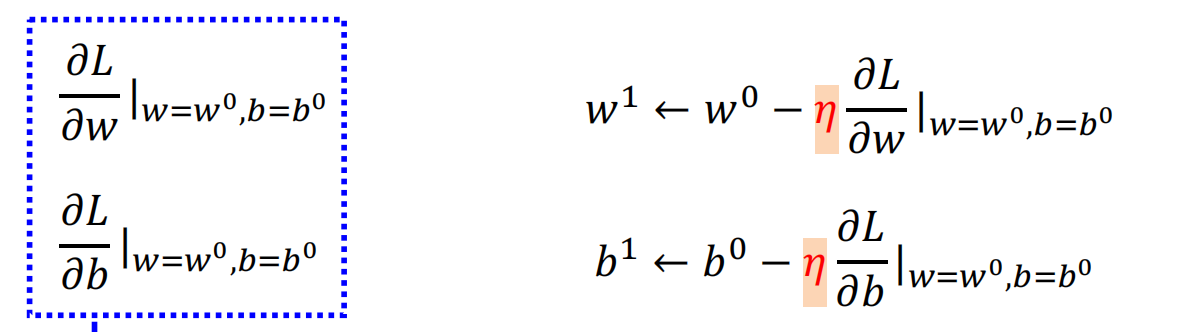
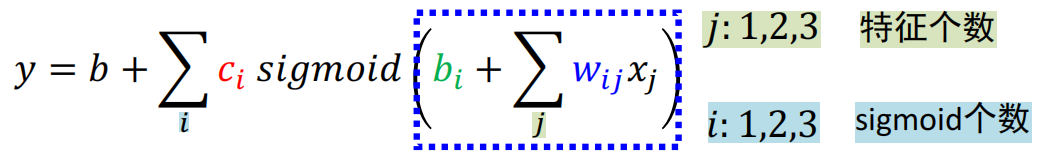
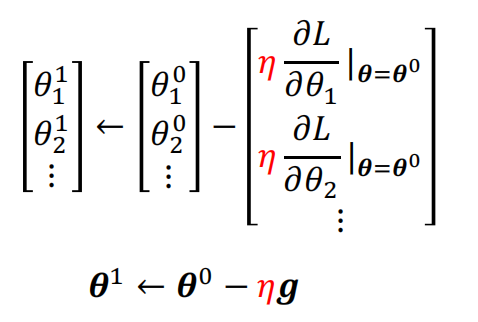


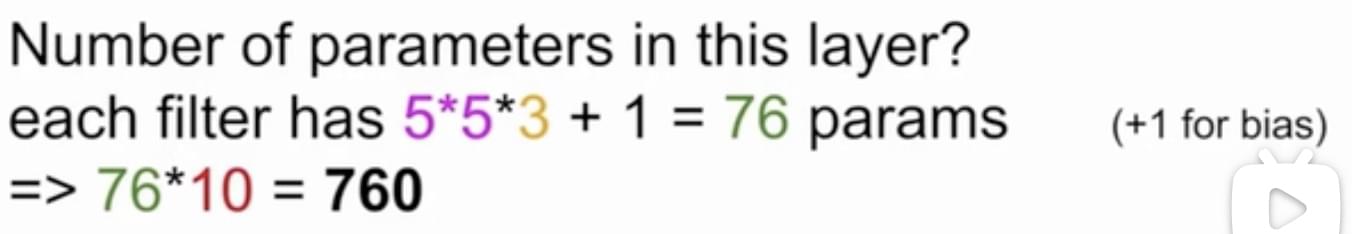
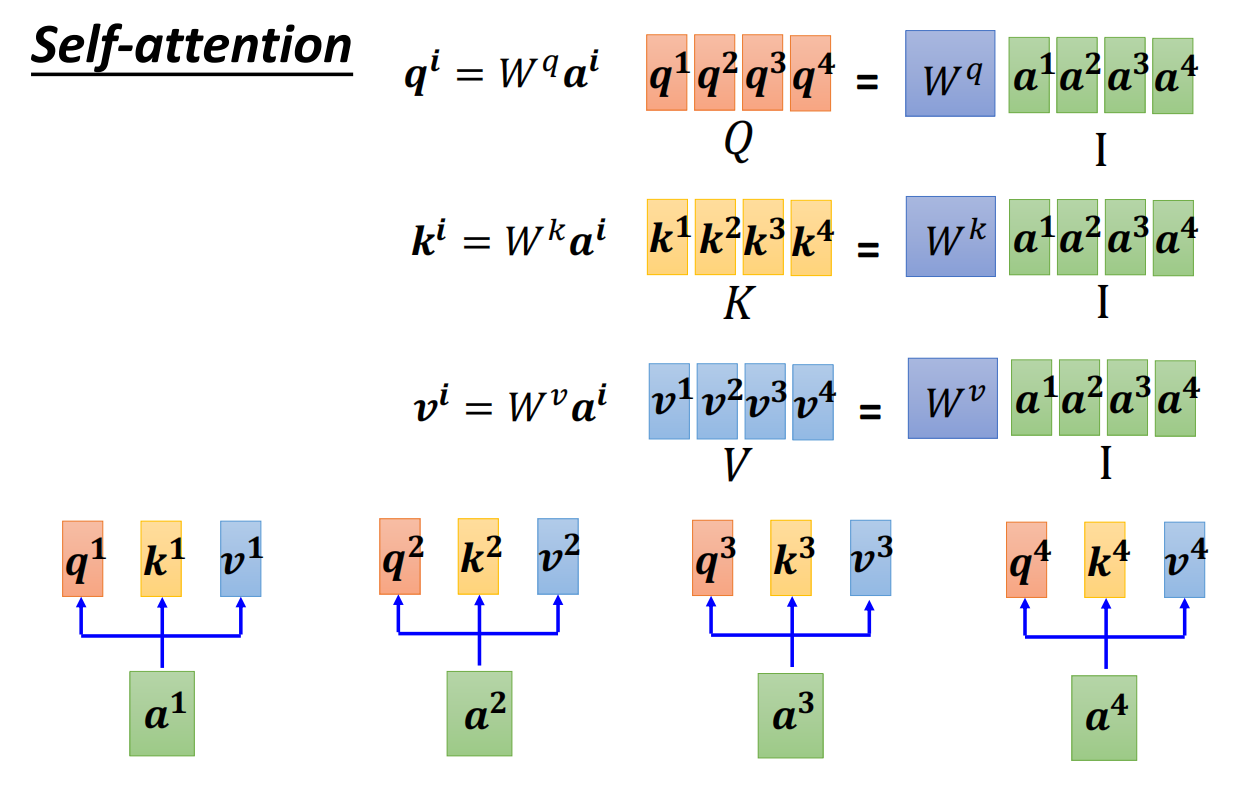
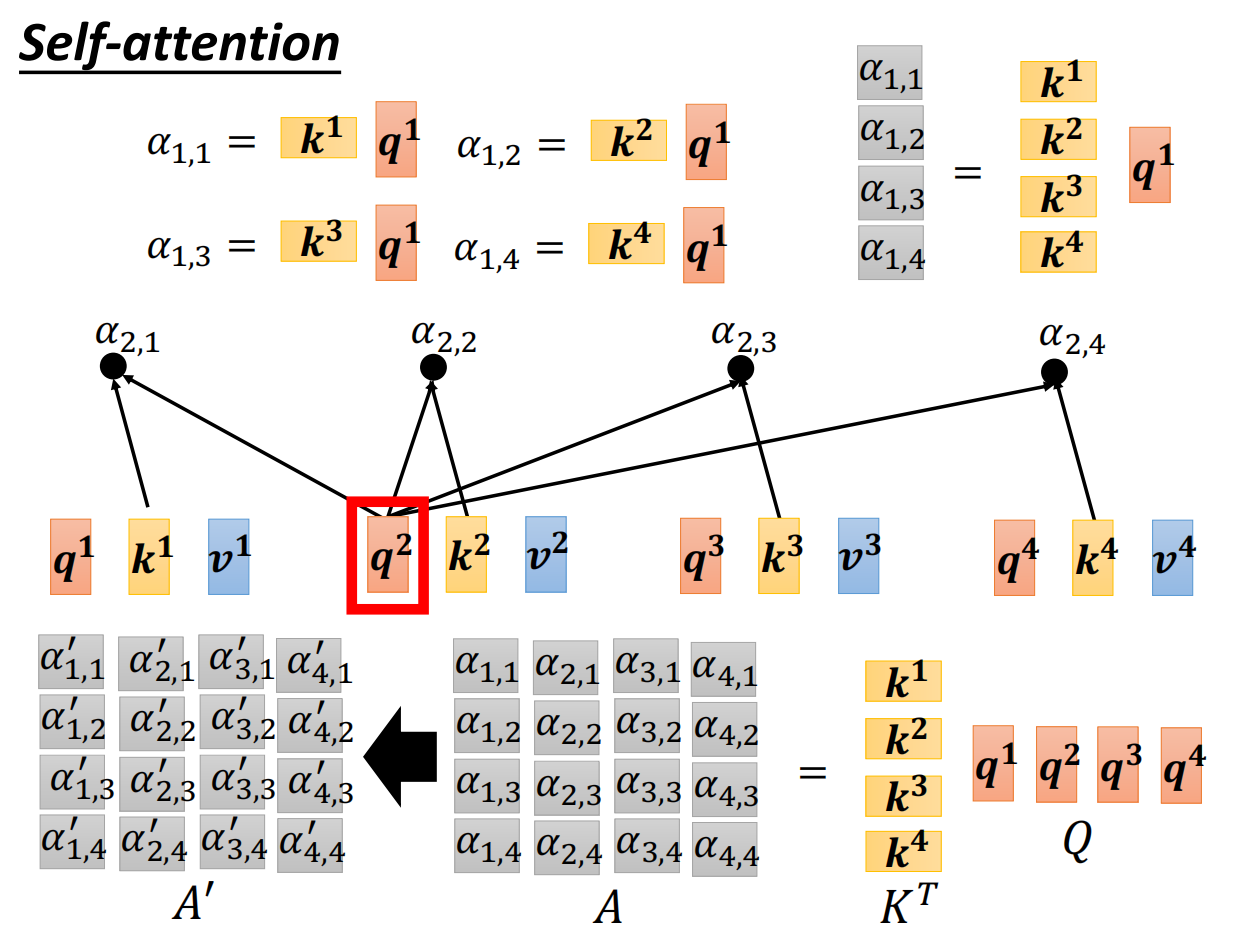
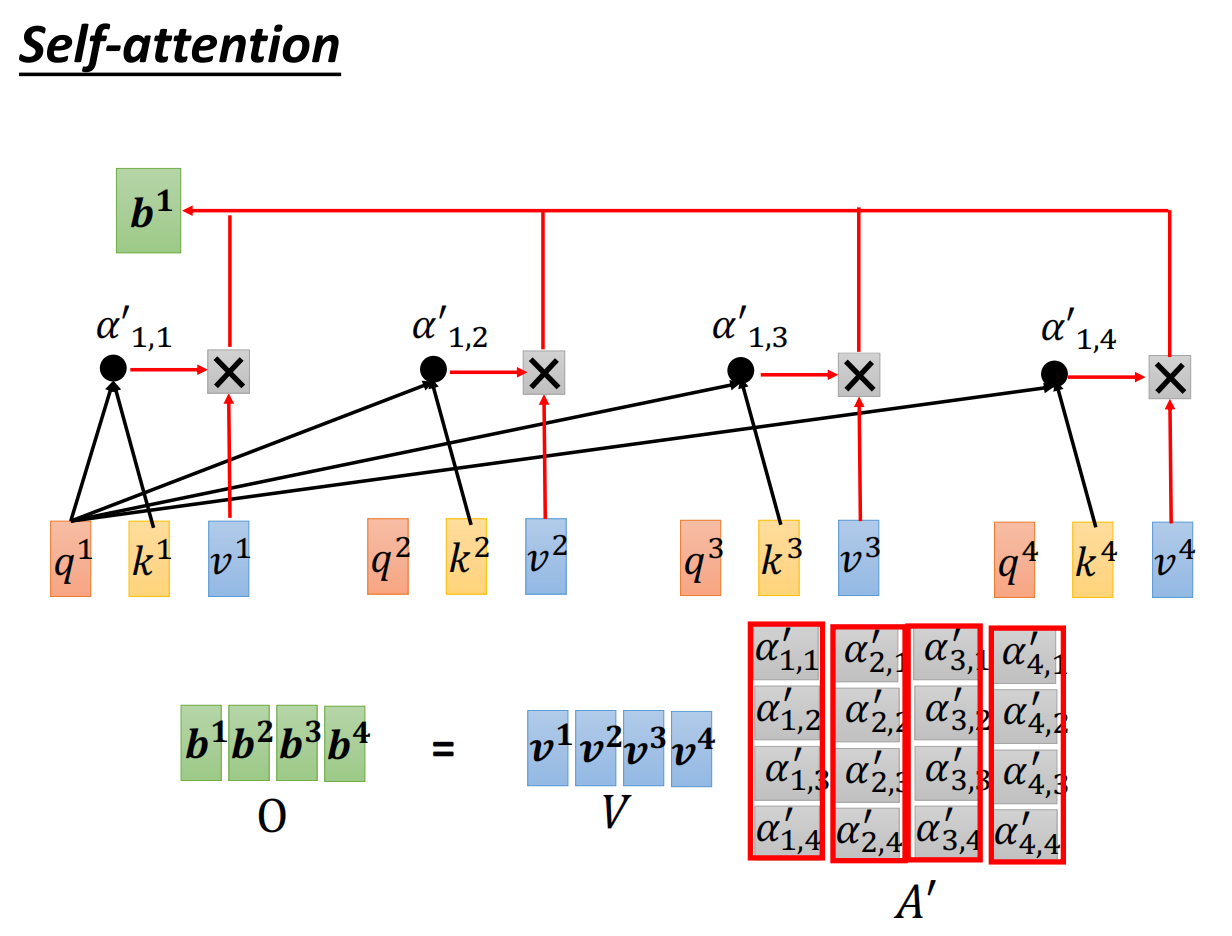 总过程:
总过程: