详解变分自编码器
VAE
信息论
信息量
\(I(x)=-\log{P(x)}\),描述事件x中包含的信息量。
信息熵
设随机变量X~p(X),则X的熵被定义为: \[ H(p)=\mathbb{E}_{X\sim p(X)}[-\log p(X)]. \] 当X为离散随机变量时, \[ H(p)=-\sum_{i=1}^{n}p(x_i)\log p(x_i) \] 熵的数学化理解: 编码随机变量所需的最短平均编码长度 即对于更大概率的事件,采用更短的编码(同Huffman编码思路一致)。
证明: 假设编码的字符集大小为\(D\),若采用二进制编码,则\(D=2\). 假设存在需要编码的\(m\)个事件,每个事件的编码长度为\(l_i\). 根据编码理论中的Kraft–McMillan Inequality,在给定的码字字长下能够成功编码,当且仅当: \[ \sum_{i=1}^{m}D^{-l_i}\leq 1. \] 转为如下优化问题: \[ \min_{l_i}\sum_{i=1}^{m}p(x_i)l_i \] \[\sum_{i=1}^{m}D^{-l_i}\leq 1.\] 利用Lagrangian multiplier进一步求解带约束的优化问题,即: \[ J=\sum_{i=1}^{m}p(x_i)l_i+\lambda(\sum_{i=1}^{m}D^{-l_i}-1). \] 得: \[ l_i^{*}=-\log_Dp(x_i). \] 若采用二进制编码,即: \[ \sum p(x_i)l_i^{*}=-\sum p(x_i)\log p(x_i)=H(p). \] 其中,熵的单位为
bit,若采用\(e\)为底数,则熵的单位为nat.
交叉熵
熵的定义: \[ H(p)=\mathbb{E}_{X\sim p(X)}[-\log p(X)], \] 设\(p\)为真实分布,\(q\)为\(p\)的近似分布,则交叉熵被定义为: \[ H(p,q)=\mathbb{E}_{X\sim p(X)}[-\log q(X)] \] 熵\(H(p)\)是随机变量\(X\)的最优期望编码长度,有: \[ \mathbb{E}_{X\sim p(X)}[-\log p(X)]\leq \mathbb{E}_{X\sim p(X)}[-\log q(X)] \]
转为证明: \[ \sum_{i=1}^{n}p(x_i)[\log p(x_i)-\log (q(x_i))]\geq 0. \] 由于对任意\(x>0\),有:\(\ln x\leq x-1\),所以\(-\log_{2}x\geq\frac{1-x}{\ln 2}\) 因此 \[ \sum_{i=1}^{n}p(x_i)[\log p(x_i)-\log (q(x_i))] \\ =\sum_{i=1}^{n}p(x_i)[\log (\frac{p(x_i)}{q(x_i)})] \\ \geq \frac{1}{\ln 2}\sum_{i=1}^{n}p(x_i)(1-\frac{q(x_i)}{p(x_i)}) \\ =\frac{1}{\ln 2}(\sum_{i=1}^{n}p(x_i)-\sum_{i=1}^{n}q(x_i)) \\ =0 \] 交叉熵在机器学习中,作为损失函数。利用\(q(x)\)逼近\(p(x)\),使得交叉熵最小。
KL Divergence
对于离散随机变量,分布\(p\)和\(q\)的\(KL\)散度定义如下: \[ D_{KL}(p\Vert q)=-\sum_{i=1}^{n}p(x_i)·\log \frac{q(x_i)}{p(x_i)} \] 展开为: \[ D_{KL}(p\Vert q)=-\sum_{i=1}^{n}p(x_i)·\log \frac{q(x_i)}{p(x_i)} \\ =-\sum_{i=1}^{n}p(x_i)·\log q(x_i)+\sum_{i=1}^{n}p(x_i)·\log p(x_i) \\ =H(p,q)-H(p). \] 含义为:利用\(q\)编码\(X\)导致的额外编码长度。恒有: \[ D_{KL}(p\Vert q)\geq 0. \] \(KL\)散度优化策略:
若真实分布\(p\)恒定,则优化\(KL\)散度,等价于优化交叉熵;多出现于辨别模型,此时可直接优化交叉熵;
若真实分布\(p\)不恒定,则优化\(KL\)散度,会同时改变交叉熵和熵的值,使得\(p\)和\(q\)相互接近;多出现于生成模型,此时需要直接优化\(KL\)散度。
估计方法
最大似然估计(MLE)
假设有训练集\(X\),设其为离散随机变量,且其可能的取值为\(\{x_1,...,x_n\}\). 目标是:寻找一个最优的\(\theta_{MLE}\),使得:\(P(X|\theta_{MLE})\)最大化。即在参数\(\theta_{MLE}\)下,训练集\(X\)出现概率最大。
有似然函数: \[ L(\theta)=P(X|\theta) \\ =P(x_1|\theta)·P(x_2|\theta)···P(x_n|\theta) \\ =\prod_{i=1}^{n}P(x_i|\theta). \] 则有: \[ \theta_{MLE}=argmax_{\theta}L(\theta) \\ =argmax_{\theta}\log L(\theta) \\ =argmin_{\theta}-\log L(\theta) \\ =argmin_{\theta}-\sum_{i=1}^{n}\log P(x_i|\theta). \]
区分Probability和Likelihood:
给定一个\(P(X|\theta)\),若称为Probability,则\(\theta\)已知,\(X\)是变量,\(P(X|\theta)\)是一个关于\(X\)的函数。关心的是:对任意的\(X\),其出现的概率;
给定一个\(P(X|\theta)\),若称为Likelihood,则\(X\)已知,\(\theta\)是变量,\(P(X|\theta)\)是一个关于\(\theta\)的函数。关心的是:寻找一个\(\theta\),使得在该\(\theta\)下,\(X\)出现的概率最大。
最大后验估计(MAP)
对比:MLE通过优化参数\(\theta\),使得训练集\(X\)出现的概率最大化。MAP嵌入先验知识。 假设\(\theta\)是服从某先验分布的随机变量,令:\(\theta_{MAP}=argmax_{\theta}P(\theta|X)\). 在\(P(\theta|X)\)中,\(X\)是已观测到的随机变量,\(\theta\)是未观测到的随机变量。使用贝叶斯公式: \[ \theta_{MAP}=argmax_{\theta}P(\theta|X) \\ =argmax_{\theta}\frac{P(X|\theta)P(\theta)}{P(X)} \\ =argmax_{\theta}P(X|\theta)P(\theta) \\ =argmax_{\theta}P(\theta)\prod_{i=1}^{n}P(x_i|\theta) \\ =argmax_{\theta}\log(P(\theta)\prod_{i=1}^{n}P(x_i|\theta)) \\ =argmax_{\theta}(\log(P(\theta))+\sum_{i=1}^{n}\log(P(x_i|\theta))) \\ =argmin_{\theta}(-\log(P(\theta))-\sum_{i=1}^{n}\log(P(x_i|\theta))). \] 注意点:
若先验分布\(\theta\)服从均匀分布,则\(P(\theta)\)为常数,此时\(\theta_{MAP}=\theta_{MLE}\);
MAP可视作:MLE增加了一个关于参数的先验分布的正则项\(\log(P(\theta))\).
3.损失函数
3.1 MSE
训练集中\(n\)个样本,每个样本有\(d\)个特征,那么样本\(i\)的特征向量记为:\(\vec{x_i}\in \mathbb{R}^{d}\),标注记为:\(y_i\in \mathbb{R}.\) 设模型参数\(\vec{w}\in \mathbb{R}^{d},b\in \mathbb{R}\).显然,模型对样本\(i\)的输出为: \[ f(\vec{x_i})=\vec{w}·\vec{x_i}+b. \] 损失函数为: \[ l(y_i,f(\vec{x_i}))=\frac{1}{2}{(y_i-f(\vec{x_i}))}^{2}. \]
几何角度:最小化样本拟合值与真实值之间欧式距离的平方。 模型会更加重视拟合效果差的样本点,因此异常值影响较大。
概率角度: 假设存在某\(\vec{w'}\)和\(b'\),使得数据集中各样本\((\vec{x_i},y_i)\)满足:\(y_i=\vec{w'}·\vec{x_i}+b'+\epsilon\)。其中\(\epsilon\)是随机变量,代表样本中的噪声分布。
假设噪声服从高斯分布,即:\(\epsilon\sim\mathcal{N}(0,{\sigma}^{2})\).则: \(y_i\sim\mathcal{N}(\vec{w'}·\vec{x_i}+b',{\sigma}^{2})\). 那么: \[ p(y_i|\vec{x_i'},\vec{w'},b')=\frac{1}{\sqrt{2\pi{\sigma}^{2}}}\exp(-\frac {(y_i-{(\vec{w'}·\vec{x_i}+b')}^{2})}{2{\sigma}^{2}}). \]
利用MLE估计\(\vec{w'}\)和\(b'\)的真值,则极大似然函数为: \[ L(\vec{w'},b)=\prod_{i=1}^{n}p(y_i|\vec{x_i};\vec{w},b). \] 有: \[ -\log{L(\vec{w'},b)}=-\sum_{i=1}^{n}\log{p(y_i|\vec{x_i};\vec{w},b)} \\ =-n·\log{\frac{1}{\sqrt{2\pi{\sigma}^{2}}}}+\frac{1}{2{\sigma}^{2}}\sum_{i=1}^{n}{(y_i-(\vec{w'}·\vec{x_i}+b'))}^{2}. \] 此时,最小化\(-\log{L(\vec{w},b)}\)等价于:最小化MSE.
0-1 Loss
适用于二分类问题,假设数据标注:\(y_i\in\{-1,+1\}\).考虑如下0-1损失函数: \[\mathcal{l}(y_i,f(\vec{x_i}))\begin{cases} 0 & if\quad y_i·f(\vec{x_i})>0 \\ 1 & if\quad y_i·f(\vec{x_i})\leq 0 \\ \end{cases} \] 即:\(y_i\)与\(f(\vec{x_i})\)同号时,视作模型预测正确,损失为0;否则,视作模型预测错误,损失为1.
数据集上的Empirical Risk是: \[ \mathcal{L}=\frac{1}{n}\sum_{i=1}^{n}\mathcal{l}(y_i,f(\vec{x_i})) \\ =\frac{1}{n}\sum_{i=1}^{n}1_{\{y_i·f(\vec{x_i})\leq 0\}}. \] 由于该损失函数非凸,不连续,且无法应用基于梯度的优化方法。穷尽搜索的搜索空间大小为\(2^{n}\),此时,最小化0-1损失是一个NP-hard问题。
Logistic Loss
二分类场景中,假设\(y_i\)服从关于\(\vec{x_i}\)的伯努利分布,令:\(y_i\in\{0,1\}\),\(P(y_i=1|\vec{x_i})=p_i\),则:\(P(y_i=0|\vec{x_i})=1-p_i\).即: \[ P(y_i|\vec{x_i})=p_i^{y_i}·(1-p_i)^{1-y_i}. \]
利用MLE估计未知参数\(p_i\)有: \[ p_i^{*}=argmin_{p_i}-\sum_{i=1}^{n}\log{[p_i^{y_i}·(1-p_i)^{1-y_i}]} \\ =argmin_{p_i}\frac{1}{n}\sum_{i=1}^{n}[-y_i·\log{p_i}-(1-y_i)·\log{(1-p_i)}]. \] 假设\(p_i\)是一个关于\(\vec{x_i}\)的函数,即:\(p_i=f(\vec{x_i})=P(y_i=1|\vec{x_i})\)。假设:\(f(\vec{x_i})\)是由未知参数\(\vec{w}\)和\(b\)参数化的,即:\(f(\vec{x_i};\vec{w},b)\).
则有损失函数: \[ \mathcal{l}(y_i,f(\vec{x_i};\vec{w},b))=-y_i·\log{f(\vec{x_i};\vec{w},b)}-(1-y_i)\log{[1-f(\vec{x_i};\vec{w},b)]}. \] 最小化该损失函数,以求出最优参数\(\vec{w}^{*}\)和\(b^{*}\),使得:数据集出现的概率最大化(经验风险最小化)。利用\(f(\vec{x_i};\vec{w}^{*},b^{*})\)预测新样本的类别。
Logistic Function:
\[ S(\vec{x_i};\vec{w},b)=\frac{1}{1+e^{-\vec{w}·\vec{x_i}+b}}. \] 该函数满足以下要求: - \(f(\vec{x_i};\vec{w},b)\)连续可导,可基于梯度来优化损失; - 值域在[0,1]之间。
令\(f(\vec{x_i};\vec{w},b)=S(\vec{x_i};\vec{w},b)\),则称得到的损失\(\mathcal{l}(y_i,f(\vec{x_i};\vec{w},b))\)为Logistic Loss.
对比: * MSE:假设\(y_i\)服从关于\(\vec{x_i}\)的高斯分布,通过MLE得到; * Logistic Loss:二分类场景,假设\(y_i\)服从关于\(\vec{x_i}\)的伯努利分布,通过MLE得到。
变分自编码器(VAE)
动机
主成分分析
原始数据标准化处理: 假设有\(n\)个数据,\(m\)个指标,第\(i\)个评价对象的第\(j\)个指标的取值为\(a_{ij}\)。转为: \[ \tilde{a_{ij}}=\frac{a_{ij}-\mu_{j}}{s_j}, i=1,2,...,n;j=1,2,...,m. \] 其中,\(\mu_j,s_j\)分别为指标\(j\)的均值和样本标准差。 称: \[ \tilde{x_j}=\frac{x_j-\mu_j}{s_j},j=1,2,...,m \] 为标准化指标向量。
计算相关系数矩阵\(R=(r_{ij})_{n\times m}\),有: \[ r_{ij}=\frac{\sum\limits_{k=1}^{n}\tilde{a_{ki}}·\tilde{a_{kj}}}{n-1},i,j=1,2,...,m. \]
计算特征值和特征向量。 计算相关系数矩阵\(R\)的特征值\(\lambda_1\geq \lambda_2\geq ...\geq \lambda_m\geq0\),对应的特征向量\(\vec{w_1},\vec{w_2},...,\vec{w_m}\),其中:\(\vec{w_j}=\begin{pmatrix} w_{1j} \\ w_{2j} \\ \vdots \\ w_{mj} \end{pmatrix}\),由特征向量组成\(m\)个新的指标变量: \[ y_1=(\tilde{x_1},\tilde{x_2},...,\tilde{x_m})·\vec{w_1}=w_{11}·\tilde{x_1}+w_{21}·\tilde{x_2}+...+w_{m1}·\tilde{x_m}, \\ y_2=(\tilde{x_1},\tilde{x_2},...,\tilde{x_m})·\vec{w_2}=w_{12}·\tilde{x_1}+w_{22}·\tilde{x_2}+...+w_{m2}·\tilde{x_m}, \\ \vdots \\ y_m=(\tilde{x_1},\tilde{x_2},...,\tilde{x_m})·\vec{w_m}=w_{1m}·\tilde{x_1}+w_{2m}·\tilde{x_2}+...+w_{mm}·\tilde{x_m}, \] 式中:\(y_1\)为第1主成分;\(y_2\)为第2主成分;...;\(y_m\)为第m主成分。
取前\(l\)个最大特征根对应的特征向量\(w_1,...,w_l\),组成映射矩阵\(W\). 有: \[ {(y_1,...,y_l)}^{T}=(x_1,...,x_m)·W_{m\times l} \]
对每个\(m\)维向量,按照如下方法进行降维: \[ (\vec{x})_{1\times m}(W)_{m\times l}=(\vec{y})_{1\times l} \]
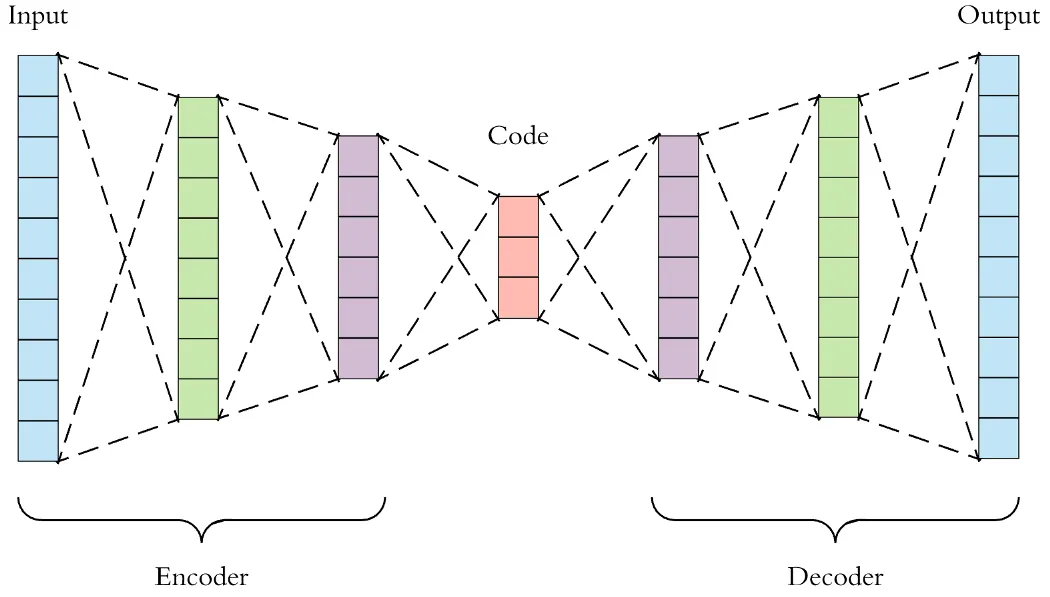
自编码器(Autoencoder)
记\(X\)为整数个数据集的集合,\(x_i\)是数据集中的一个样本。 - 编码器:\(z=g(X)\),输出\(z\)的维度远小于输入\(X\)的维度; - 解码器:\(\tilde{X}=f(z)\),通过编码\(z\)还原出\(\tilde{X}\). - 损失函数:重构误差:\(\mathbb{l}={\lVert X-\tilde{X} \rVert}^{2}\)
例子:输入图片\(X\in \mathbb{R}^{C\times H\times W}\),训练一个自编码器。
编码器\(z=g(X)\)将每个图片编码成\(z\in \mathbb{R}^{d}\);
解码器利用\(z\)将输入的图片重建为\(\tilde{X}\in\mathbb{R}^{C\times H\times W}\).
将解码器\(g:\mathbb{R}^{d}\rightarrow\mathbb{R}^{C\times H\times W}\)视作生成模型:
输入低维向量\(z\),输出高维图片数据\(X\).
对于绝大多数随机生成的\(z\),\(f(z)\)只会生成无意义的噪声;
VAE思想:显性地对\(z\)的分布\(p(z)\)建模。
推导
生成数据的步骤:
从先验分布\(p(z)\)采样得到一个\(z_i\);
根据\(z_i\),从条件分布\(p(X|z_i)\)中采样得到一个数据点.
Decoder结构
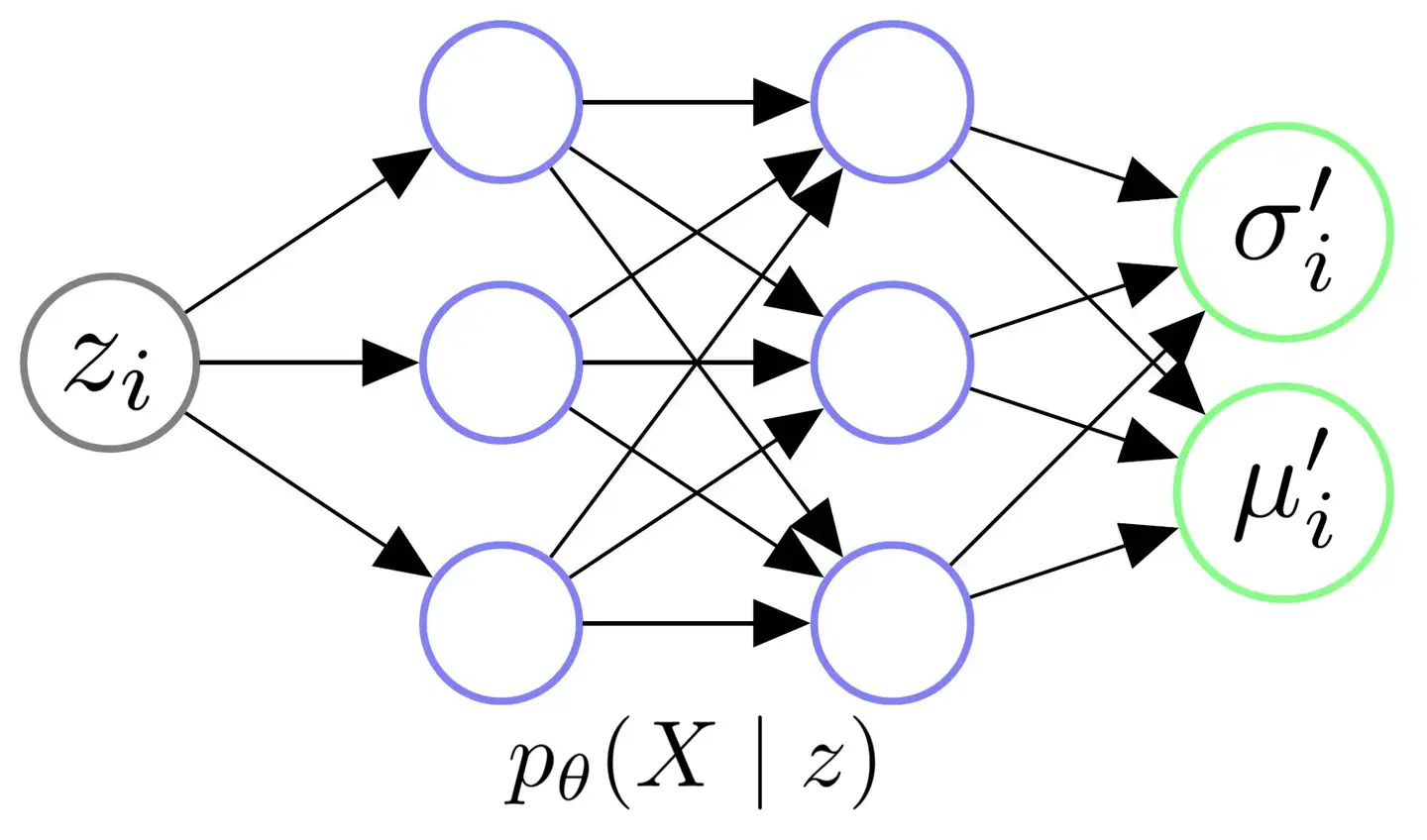
目标:输入从\(\mathcal{N}(0,I)\)中采样得到的\(z_i\),希望Decoder学会一个映射,输出\(z_i\)对应的\(X\)的分布\(p_\theta(X|z_i)\).
假设:给定任意\(z_i\)后,对应的\(X\)服从某个各维度独立的多元高斯分布,即: \[ p_\theta(X|z_i)=\mathcal{N}(X|{\mu_i}^{'}(z_i;\theta),{\sigma_{i}^{'}}^{2}(z_i;\theta)*I). \] 那么有: \[ p_\theta(X)=\int_{z}p_\theta(X|z)p(z)dz \\ \approx\frac{1}{m}\sum\limits_{j=1}^{m}p_\theta(X|z_j). \] 因此,需要从\(p(z)=\mathcal{N}(z|0,I)\)中大量采样\(z_i\),以计算\(p_\theta(X)\)。
例子:我们的图片集是世界上所有的猫;那么抽样得到的一个\(z_i\)可能代表颜色为橘色,耳朵为立耳的猫;而下次抽样得到的另一个\(z_j\)可能代表颜色为白色,耳朵为折耳的猫。
假设:这类立耳橘猫的图片像素值的分布\(X|z_i\)服从一个多元高斯分布: > \mathcal{N}({\mu_i}^{'},{\sigma_i^{'}}^{2}*I) > 那么: 1. Decoder 通过神经网络,将 $z_i$ 变换为适当的 ${\mu_i}^{'}$ 和 ${{\sigma_i}^{'}}^{2}$,得到多元高斯分布; 2. 之后从 $\mathcal{N}({\mu_i}^{'},{{\sigma_i}^{'}}^{2}*I)$ 中采样,生成立耳橘猫的图片。
问题:直接采样代价极大。由于\(x_i\)高维,因此\(z_i\)维度不太低。对于某个\(x_i\),与之强相关的\(z_i\)数量相对有限,因此需要进行大量的采样,才能知道:哪一些\(z_i\)是与哪一些\(x_i\)对应着的。 解决思路:在Encoder中引入后验分布\(p_\theta(z|x_i)\).
Encoder引入后验分布
思路:假设当前有后验分布\(p_\theta(z|x_i)\): 1. 前向传播时,将\(x_i\)喂给Encoder,计算\(z|x_i\)服从的分布; 2. 从该分布中采样出\(z_i\)(采样得到的\(z_i\)基本都与\(x_i\)相关),喂给Decoder,得到\(X|z_i\)的分布。
计算\(p_\theta(z|x_i)\): 尝试贝叶斯公式: \[ p_\theta(z|x_i)=\frac{p_\theta(x_i|z)p(z)}{p_\theta(x_i)} \\ =\frac{p_\theta(x_i|z)p(z)}{\int_{z'}p_\theta(x_i|z')p(z')dz'}. \] 要估计积分,需要从\(p(z)\)中大量采样\(z_i\),代价大,不可行。
解决思路:利用似然\(p_\theta(X|z)\)和先验分布\(p(z)\)都服从高斯分布的假设,可证明:真实的后验分布\(p_\theta(z|X)\)也服从高斯分布。
令近似的后验分布\(q_\phi(z|x_i)\)对任意\(x_i\)都有: \[ q_\phi(z|x_i)=\mathcal{N}(z|\mu(x_i;\phi),\sigma^{2}(x_i,\phi)*I) \] 也是一个各维度独立的多元高斯分布。
整体架构
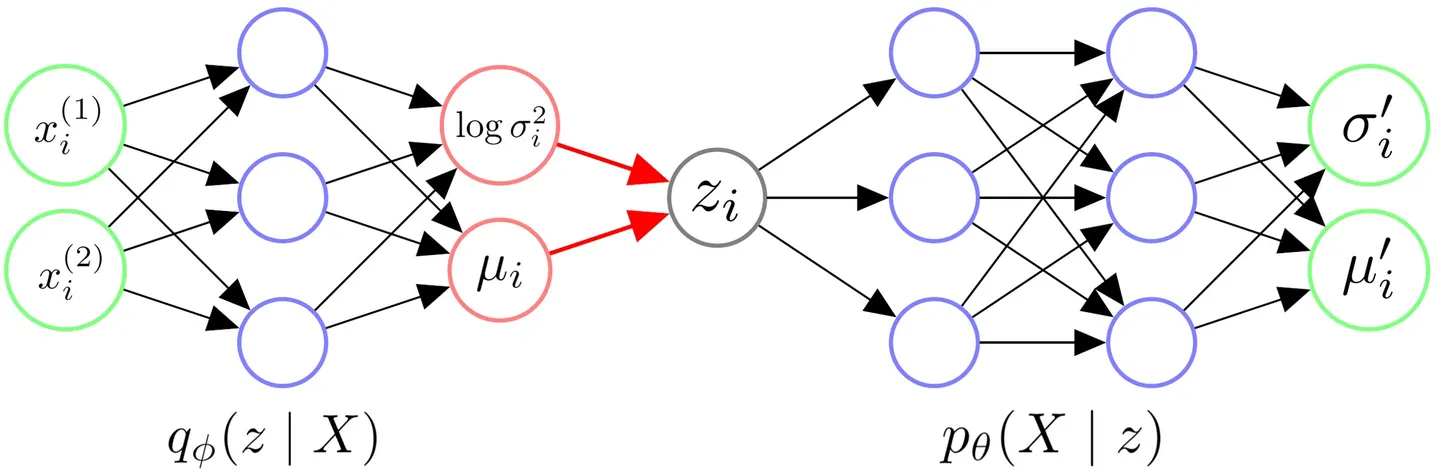
- 输入一个数据点\(x_i\),通过Encoder,得到隐变量\(z\)服从的近似后验分布\(q_\phi(z|x_i)\)的参数;(将后验分布视作一个各维度独立的高斯分布,这里输出高斯分布的参数{{\sigma_i}^{2}}和\mu_i)
- 从对应的高斯分布采样一个\(z_i\),代表与\(x_i\)相似的一类低维样本;
- 将采样的一个\(z_i\)输入Decoder,得到似然的分布\(p_\theta(X|z_i)\);(将似然分布也视作一个各维度独立的高斯分布,输出参数{{{\sigma_i}^{'}}^{2}}和{\mu_i}^{'};
- 从对应的分布中采样,生成\(x_i\)对应的重建数据\(X_i\)。
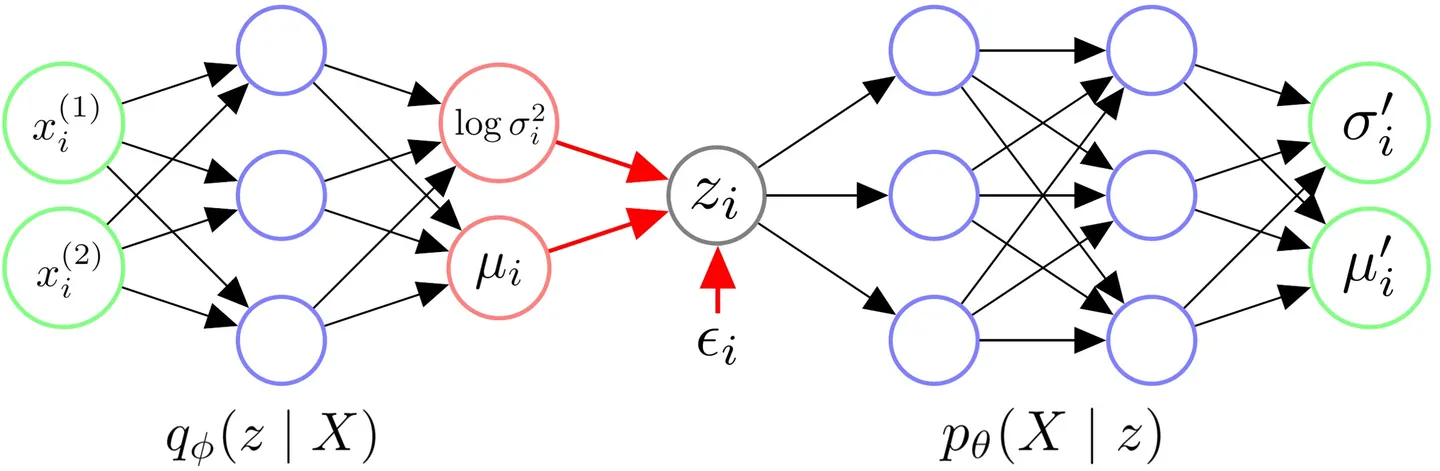
重参数化技巧
起因:前向传播过程中,调用了“采样函数”,无法反向传播。 解决方案:为了网络的正常训练,采样步骤改为: 获得后验分布\(q_\phi(z|x_i)\)的参数\({\sigma_i}^{2}\)和\(\mu_i\)后,先从\(\mathcal{N}(0,I)\)中采样得到一个\(\epsilon_i\),令: \[ z_i=\mu_i+\sigma_i\odot\epsilon_i \] 得到的\(z_i\)代表与\(x_i\)相似的一类样本。 (\(\odot\)代表逐元素相乘)
计算损失
利用MLE最大化,确定参数\(\theta\),有: \[ \log p_\theta(X)=\int_z q_\phi(z|X)\log {p_\theta}(X)dz \\ =\int_z q_{\phi}(z|X)\log{\frac{p_\theta(X,z)}{p_\theta(z|X)}}dz \\ =\int_z q_\phi(z|X)\log(\frac{p_\theta(X,z)}{q_\phi(z|X)}·\frac{q_\phi(z|X)}{p_\theta(z|X)})dz \\ =\int_z q_\phi(z|X)\log\frac{p_\theta(X,z)}{q_\phi(z|X)}dz+\int_z q_\phi(z|X)\log\frac{q_\phi(z|X)}{p_\theta(z|X)}dz \\ =\mathcal{l}(p_\theta,q_\phi)+D_{KL}(q_\phi,p_\theta) \\ \geq \mathcal{l}(p_\theta,q_\phi) \]
ELBO(Evidence Lower Boud)
\(\mathcal{l}(p_\theta,q_\phi)\)是\(\log{p_\phi(X)}\)的一个下界。 有: \[ \mathcal{l}(p_\theta,q_\phi)=\int_z q_\phi(z|X)\log\frac{p_\theta(X,z)}{q_\phi(z|X)}dz \\ =\int_z q_\phi(z|X)\log\frac{p_\theta(X,z)p(z)}{q_\phi(z|X)}dz (贝叶斯定理) \\ =\int_z q_\phi(z|X)\log\frac{p(z)}{q_\phi(z|X)}dz+\int_z q_\phi(z|X)\log{p_\theta(X,z)}dz \\ =-D_{KL}(q_\phi,p)+\mathbb{E}_{q_\phi}[\log p_\theta(X,z)]. \]
Latent Loss:\(D_{KL}(q_\phi,p)\)
由于\(q_\phi(z|X)\)和\(p(z)\)均服从各维度独立的高斯分布的假设,得到\(D_{KL}(q_\phi,p)\)的解析解: 一维上,有: \[ D_{KL}(\mathcal{N}(\mu,{\sigma}^{2})\Vert\mathcal{N}(0,1))=\int_z\frac{1}{\sqrt{2\pi{\sigma}^{2}}}\exp(-\frac{({z-\mu}^{2})}{2{\sigma}^{2}})\log\frac{\frac{1}{\sqrt{2\pi{\sigma}^{2}}}\exp(-\frac{({z-\mu}^{2})}{2{\sigma}^{2}})}{\frac{1}{\sqrt{2\pi}}\exp(-\frac{{z}^{2}}{2})}dz \\ =\int_z\mathcal{N}(\mu,{\sigma}^{2})(-\frac{({z-\mu}^{2})}{2{\sigma}^{2}}+\frac{{z}^{2}}{2}-\log{\sigma})dz \\ =-\int_z\frac{({z-\mu}^{2})}{2{\sigma}^{2}}\mathcal{N}(\mu,{\sigma}^{2})dz+\int_z\frac{{z}^{2}}{2}\mathcal{N}(\mu,{\sigma}^{2})dz-\int_z\log{\sigma}\mathcal{N}(\mu,{\sigma}^{2})dz \\ =-\frac{\mathbb{E}[{(z-\mu)}^{2}]}{2{\sigma}^{2}}+\frac{\mathbb{E}[{z}^{2}]}{2}-\log{\sigma} \\ =\frac{1}{2}(-1+{\sigma}^{2}+{\mu}^{2}-\log{{\sigma}^{2}}). \] 当均为\(d\)元高斯分布时,有: \[ D_{KL}(q_\phi(z|X),p(z))=\sum_{j=1}^{d}\frac{1}{2}(-1+{\sigma^{{(j)}^{2}}}+{\mu^{{(j)}^{2}}}-\log{\sigma^{{(j)}^{2}}}) \] 其中:${a}^{{(j)}^{2}}$代表向量\(a\)的第\(j\)个元素的平方。
Reconstruction Loss:\(\mathbb{E}_{q_\phi}[\log p_\theta(X,z)]\)
通常通过从\(q_\phi(z|X)\)中采样多个\(z_i\)来近似求解。即: \[ \mathbb{E}_{q_\phi}[\log p_\theta(X,z)]\approx\frac{1}{m}\sum\limits_{i=1}^{m}\log{p_\theta(X|z_i)}. \] 其中,\(z_i\sim q_\phi(z|x_i)=\mathcal{N}(z|\mu(x_i;\phi),{\sigma}^{2}(x_i;\phi)*I)\)