Lab0 C++ PrimerPrimer

写在开头

首先致谢CMU-db无私将这门质量极高、资源极齐全的数据库课程，以及相关基础设施（GradeScope, Discord）和课程资料（Lectures, Notes, Homework）完全开源,让一个在本科数据库课程上只学会了抽象理念和SQL语句的孩子，能踏上一条自学之路（手动狗头） 其次,感谢CS自学指南,将计算机领域的众多好课分享给我们.

本专题将详尽地记录2024 Fall对应Lecture和Lab的学习经历.

课程链接

课程主页:https://15445.courses.cs.cmu.edu/fall2024/ Discord:https://discord.com/channels/724929902075445281/752529819148877904 Gradescope:https://www.gradescope.com/courses/817458 Entry Code: WWWJZ5 (学校记得改成CMU) > In exchange for making this available to the public, we ask that you DO NOT make your project implementations public on Github or other source code repositories.

让我们开始吧.

本篇博客记录Lab概览和Project #0.

Lab概览

以下摘自CS指南:

这门课的亮点在于 CMU Database Group 专门为此课开发了一个教学用的关系型数据库 bustub，并要求你对这个数据库的组成部分进行修改，实现上述部件的功能。

具体来说，在 15-445 中,你需要在四个 Project 的推进中，实现一个面向磁盘的传统关系型数据库 Bustub 中的部分关键组件。

包括 Buffer Pool Manager (内存管理), B Plus Tree (存储引擎), Query Executors & Query Optimizer (算子们 & 优化器), Concurrency Control (并发控制)，分别对应 Project #1 到 Project #4。

值得一提的是，同学们在实现的过程中可以通过 shell.cpp 编译出 bustub-shell 来实时地观测自己实现部件的正确与否，正反馈非常足。

此外 bustub 作为一个 C++ 编写的中小型项目涵盖了程序构建、代码规范、单元测试等众多要求，可以作为一个优秀的开源项目学习。

本篇从Project #0开始.

Project #0 (2024 Fall)

2024 Fall的预实验,集中于理解和实现一个基于概率统计的大数据基数统计算法--HyperLoglog;在此过程中,熟悉C++的基本应用.

C++的基本知识可见以下两篇博客: C++中的引用、移动语义、模板、包装类、迭代器和命名空间 C++标准库：容器、动态内存、同步原语

我们从HyperLogLog的算法理论开始.

HyperLogLog算法

什么情景产生了HyperLogLog？

假设您有一个大型元素数据集，其中包含从一组基数 n 中选择的重复条目，并且想要查找 n，即基数（不同元素的数量）。例如，我们希望计算在给定的一周内访问过 Facebook 的不同用户数量，其中每个人每天登录多次。这将产生具有许多重复项的大型数据集。显而易见的方法（例如对元素进行排序，或简单地维护所看到的唯一元素集）是不切实际的，因为它们要么计算量太大，要么需要太多内存。如何处理呢？让我们逐步思考：

一个简单的估计器

我们需要一个输出估计值的算法（误差在合理范围内）。首先，生成一个具有重复条目的假设数据集如下： 1. 生成 n 个均匀分布在 0 和 1 之间的数字； 2. 将一些数字随机复制任意次数； 3. 对上述数据集，随机排序。 使用哈希函数（哈希值被规范化并在 0 和 1 之间均匀分布），设最小的哈希值为\(y_{min}=hash(x)\)，将唯一条目的数量估计为1/y_{min}. 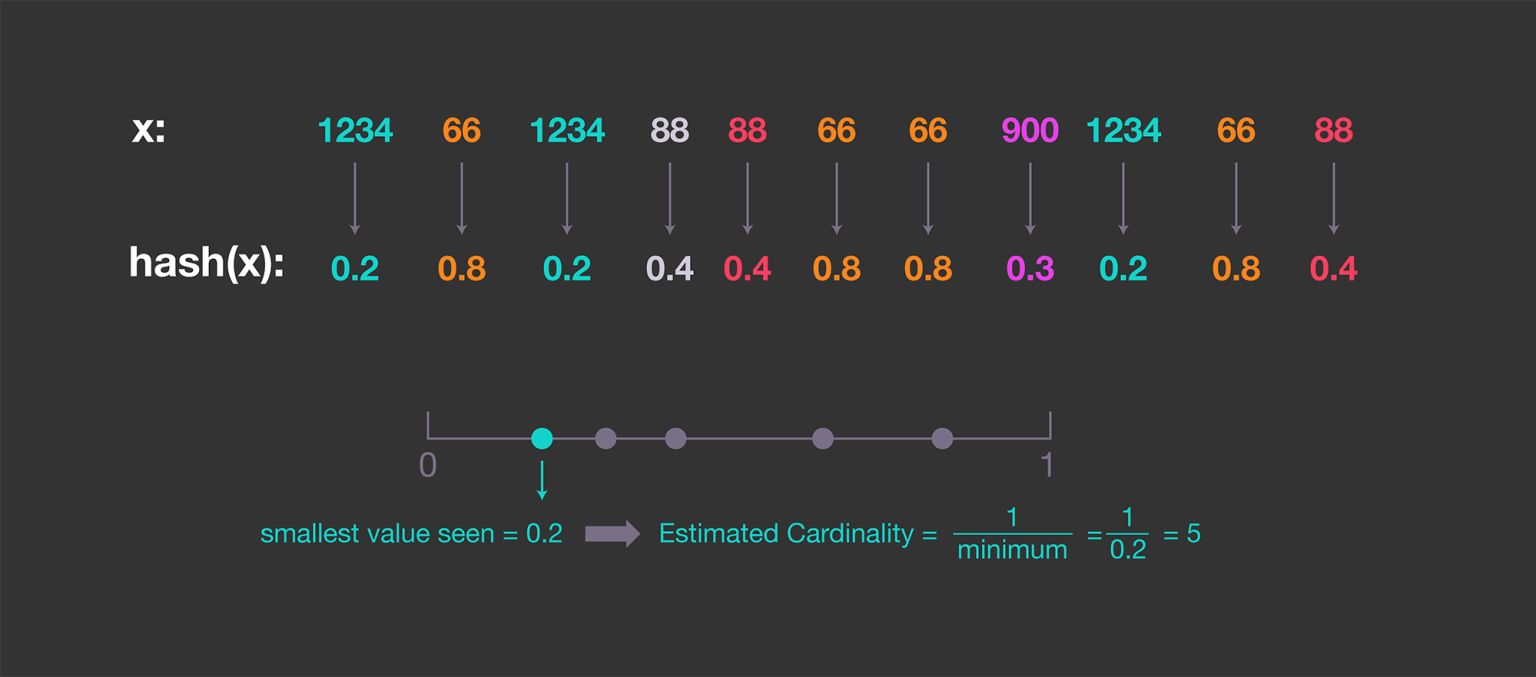然而，估计结果依赖于最小哈希值，而最小哈希值可能恰好太小，从而夸大了我们的估计。因此该方法具有高度可变性。

概率计数

为了减少之前方法中的高可变性，我们可以通过计算哈希值二进制表示中，开头的零位数来改进。 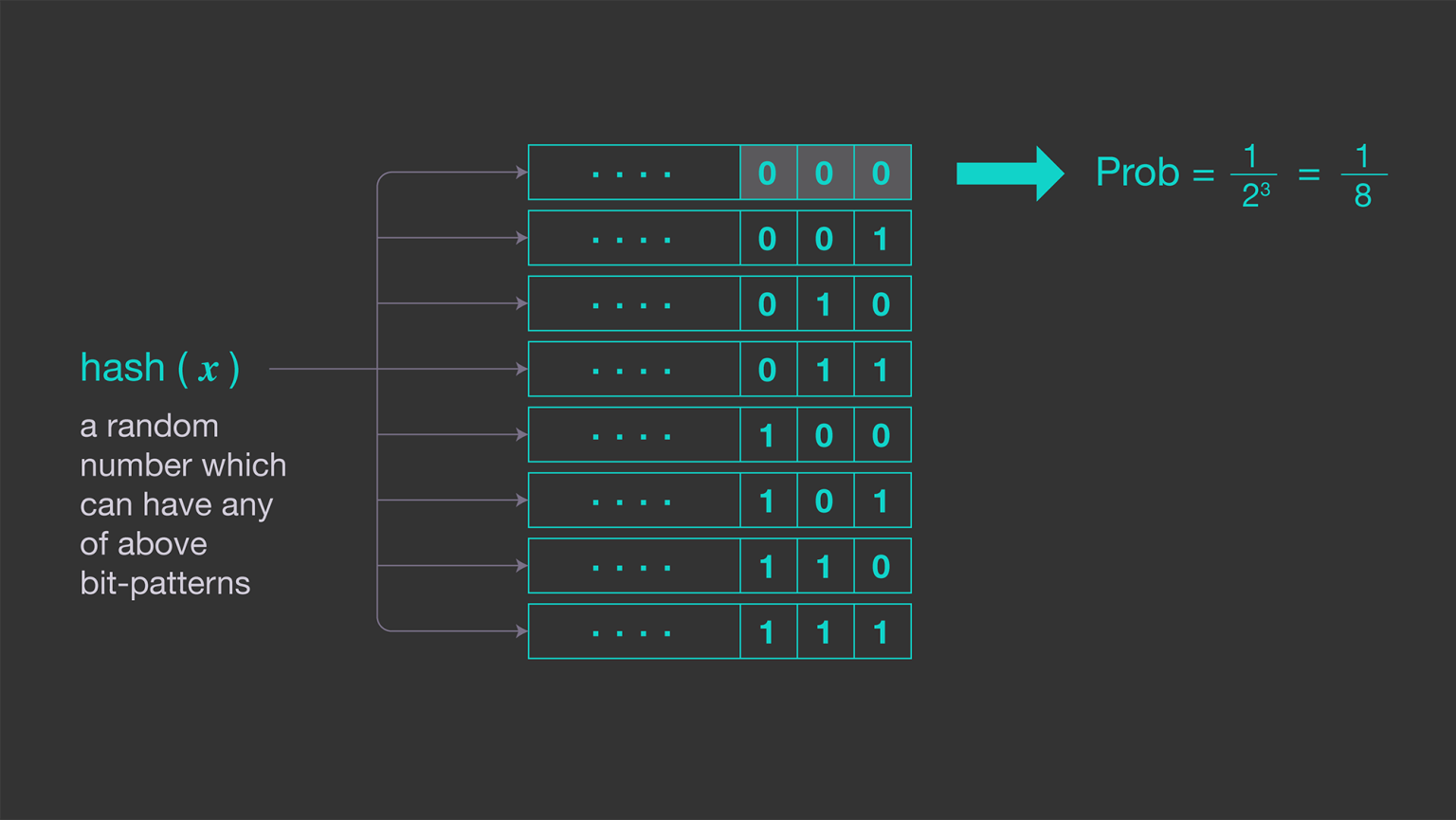平均而言，每\(2^k\)个不同条目，将出现\(k\)个连续的零序列，因此转为记录：最长的连续零序列的长度。即：

集合{\({x_1,...,x_M}\)}的基数为\(2^R\)，其中：\(R=max\){\(\rho(x_1),...,\rho(x_M)\)}，\(\rho(x_1)\)为\(hash(x_i)\)的二进制表示中，前导0的数目。

此方法有两个缺点： 1. 只能提供基数的 2 的幂估计，即结果只可能是：1，2，4，8，... 2. 如果恰巧遇到一个有太多连续前导0的条目，将产生极不准确的基数估计。

提高准确性：LogLog，采用多个估计量

上一个方法中，只采用了一个估计量，即：最大连续前导零数。为了改进，我们采用多个独立估计器，并对结果取平均，以减少单个估计器的方差。 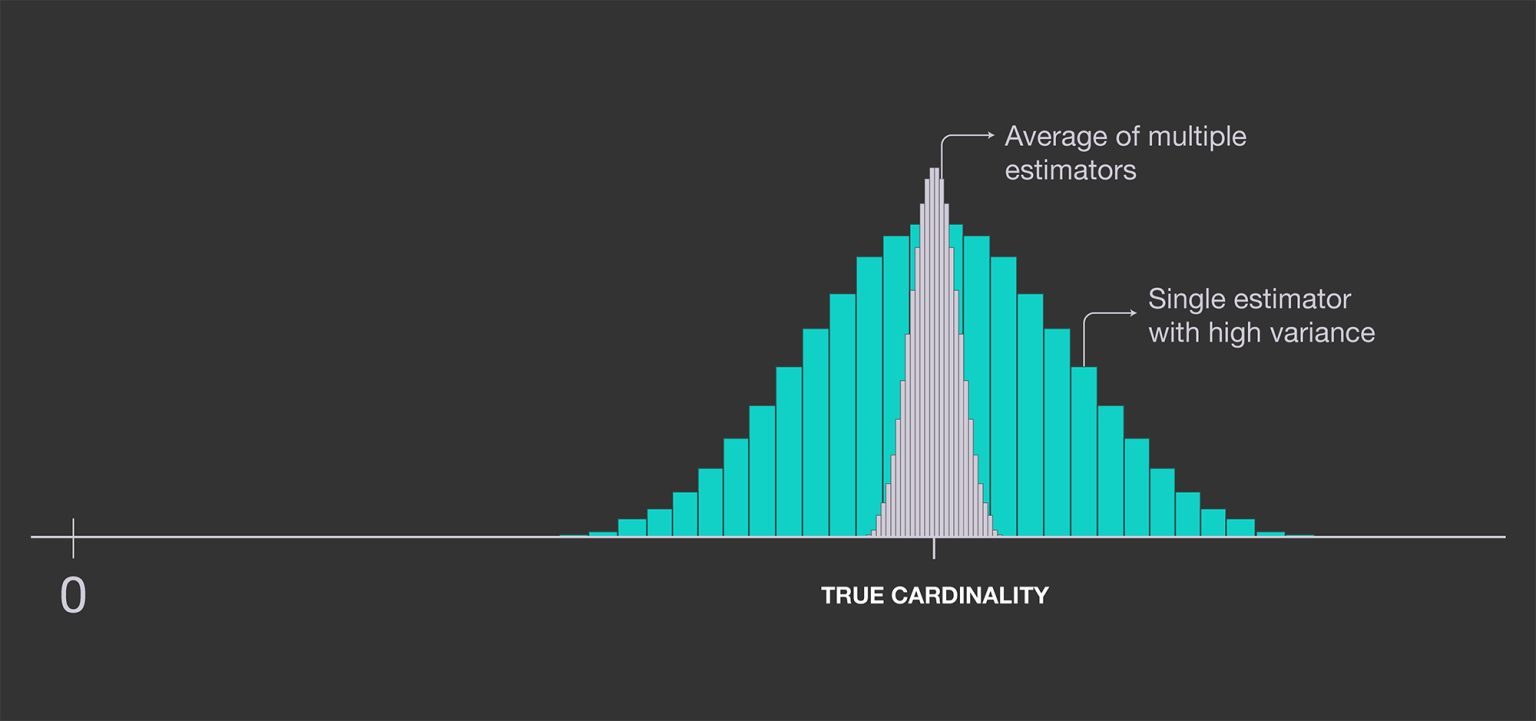可以通过使用\(m\)个独立的哈希函数实现这点，分别计算出\(R_1,...,R_m\)，取算数平均，作为\(R\)的估计值。

但是该方法对于每个条目，均需计算其相对于每个哈希函数的哈希值，计算上太昂贵。能不能采用单个哈希函数解决呢？

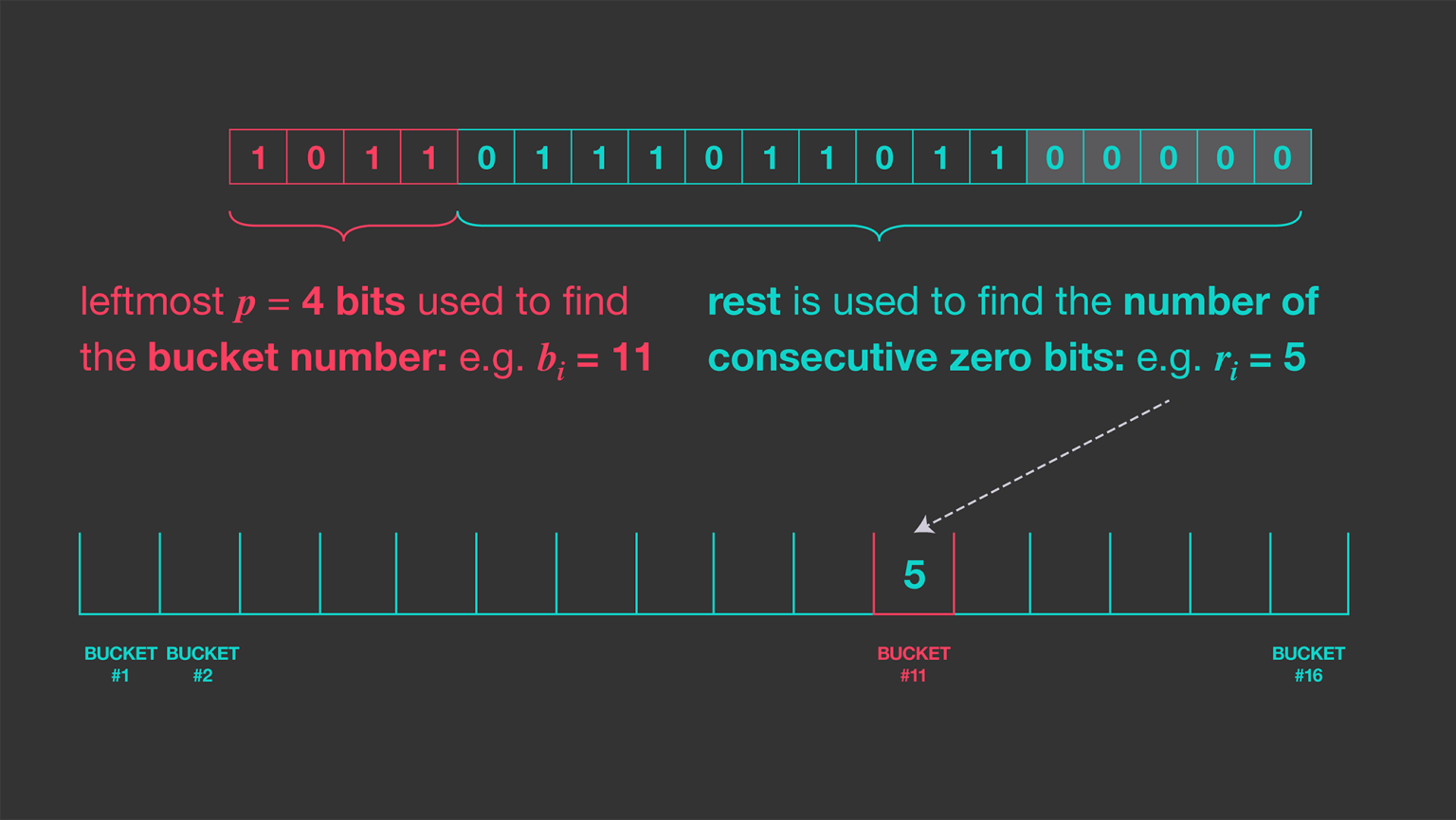
学者们提出的一个解决方案是：使用哈希值的前k位作为桶的索引；计算剩余部分的最长连续 0 序列。

如下图，假设我们传入数据的哈希值为1011 011101101100000。 1. 使用最左边的四个位(k=4)作为桶索引，它告诉我们要更新哪个存储桶（十进制为 = 11）； 2. 在剩余部分中，获取右侧的最长连续 0序列，此时该序列长度为 5； 3. 因此，使用 16 个存储桶，将存储桶编号 11 更新为值 5，如下所示。

通过拥有\(m\)个桶，我们模拟了拥有\(m\)个不同哈希函数的情况。基数估计公式如下：

\(CARDINALITY_{LogLog}=constant · m · 2^{\frac{1}{m}\sum_{j=1}^{N}R_j}\)

对于 m 个桶，这会将估计器的标准误差降低到大约 \(\frac{1.3}{\sqrt{m}}\)。 > 对于2048个桶，每个桶5位（最多可以记录32个连续0），则足以记录高达\(2^{27}\)的基数，只占用2048*5=1.2KB的内存（平均错误率大约2.8%）

更多可见以下文章: https://zhuanlan.zhihu.com/p/110364156

Lab整体实现思路

在实际应用中，一些系统将最左侧的 1 位的位置存储在寄存器中（MSB），而另一些系统则存储最右侧连续零的个数（LSB）。在这个项目中： * Task 1 采用前者;Task 2 采用后者.

Task 1

HyperLoglog定义如下: 

1
2
3
4
5
6
7
8
9
10
11
/** @brief Cardinality value. */  
size_t cardinality_;

/** @brief Number of bits. */
int16_t num_bits_;

/** @brief Number of Registers. */
uint16_t num_registers_;

/** @brief Registers. */ 
std::vector<uint64_t> registers_;
* 初始化HyperLogLog<KeyType>::HyperLogLog(int16_t n_bits)传入的n_bits是寄存器索引位数,寄存器总数为2^n_bits. * 将哈希值转为64位二进制表示; * 哈希值表示中: * 寄存器索引:从高到底的前n_bits位:即[BITSET_CAPACITY-num_bits_, BITSET_CAPACITY-1]; * 计算左侧第一个1的位置,需从:BITSET_CAPACITY - num_bits_ - 1开始,从高位向低位查找; * 寄存器当前索引对应元素的更新逻辑:如果"左侧第一个1的位置"比当前元素大,则更新.

Task2 Presto实现:密集结构

使用两个桶,即将最右侧连续零的数量这一数据,拆成两部分存储: * Dense Bucket（密集桶）: 一个固定大小的数组，存储最低位的几个比特（leading bits） * Overflow Bucket（溢出桶）: 一个哈希表:键为桶索引(和密集桶索引相同),值为超出密集桶最大容量的高位比特信息，避免溢出。 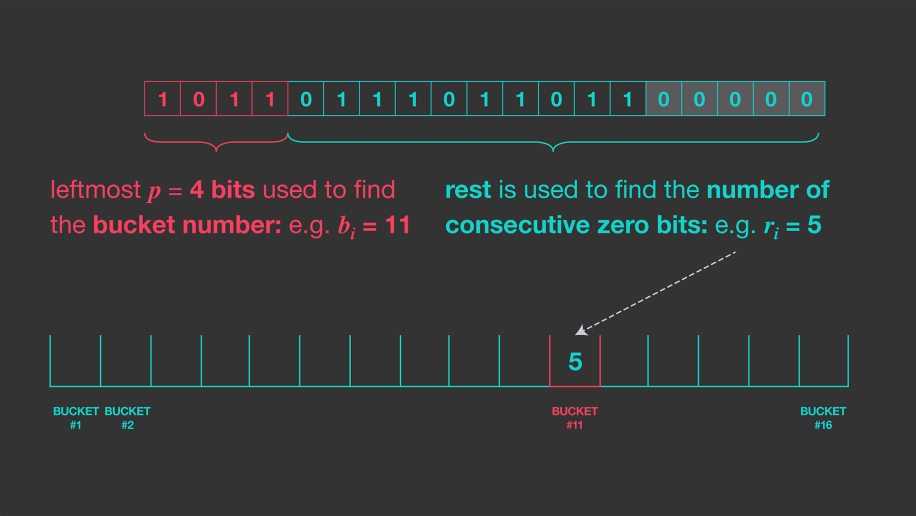如上图：如果某个值的二进制表示中，右侧连续0的数量为33，其二进制形式为0100001。在这种情况下，会将其拆分成两部分，首先是3个MSB（最高有效位）010，接着是4个LSB（最低有效位）0001。0001将存储在密集桶（Dense Bucket）中，而MSB部分010将存储在溢出桶（Overflow Bucket）中。

HyperLogLogPresto中定义如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/** @brief Capacity of the bitset stream. */
#define BITSET_CAPACITY 64

/** @brief Dense bucket size. */
#define DENSE_BUCKET_SIZE 4
/** @brief Overflow bucket size. */
#define OVERFLOW_BUCKET_SIZE 3

/** @brief Number of leading bits. */
int16_t n_leading_bits_;

/** @brief Number of Buckets. */
uint16_t num_buckets_;

/** @brief Structure holding dense buckets (or also known as registers). */
std::vector<std::bitset<DENSE_BUCKET_SIZE>> dense_bucket_;

/** @brief Structure holding overflow buckets. */
std::unordered_map<uint16_t, std::bitset<OVERFLOW_BUCKET_SIZE>> overflow_bucket_;

/** @brief Storing cardinality value */
uint64_t cardinality_;

桶中元素的更新如下: 

1
2
3
4
5
6
7
8
9
10
11
// 如果当前的连续0数量更大：更新桶的值
if ((dense_bucket_[bucket_index].to_ullong() + ((overflow_bucket_[bucket_index].to_ullong()) << 4)) <
    num_trailing_zeros) {
    std::bitset<OVERFLOW_BUCKET_SIZE> overflow_value(num_trailing_zeros >>
                                                     DENSE_BUCKET_SIZE);  // 取后4位之前的部分（转为二进制表示）
    std::bitset<DENSE_BUCKET_SIZE> dense_value(num_trailing_zeros &
                                               ((1 << DENSE_BUCKET_SIZE) - 1));  // 取后4位（转为二进制表示）

    dense_bucket_[bucket_index] = dense_value;
    overflow_bucket_[bucket_index] = overflow_value;
}

关键细节和易错点

无符号/有符号整型的处理

极易出错!!!疯狂踩坑(哭泣). 计算cardinality:头文件registers_中声明的是vector<uint64_t>,运用其中的元素reg计算:z += pow(2, -reg);

这里pow(2, -reg)会变成inf,即出现了整数下溢的bug.警惕:无符号类型不能为负!

因此应使用z += 1.0/pow(2, reg);

边界
  1. 样例EdgeTest1测试了构造函数中传入的实参n_bits为负的情况:

寄存器数目为负数是无意义的.因此构造函数应写为: 

1
HyperLogLog<KeyType>::HyperLogLog(int16_t n_bits) : cardinality_(0), num_bits_(n_bits > 0 ? n_bits : 0)

  1. 样例EdgeTest2, PrestoCase2测试了n_bits或n_leading_bits为0的情况:

这时寄存器数组registers_长度为1<<0=1, 注意计算寄存器索引/桶索引时: 

1
2
3
4
int16_t register_index =
      num_bits_ == 0 ? 0 : static_cast<int16_t>((bset.to_ullong()) >> (BITSET_CAPACITY - num_bits_));
int16_t bucket_index =
      n_leading_bits_ == 0 ? 0 : static_cast<int16_t>((bset.to_ullong()) >> (BITSET_CAPACITY - n_leading_bits_));
bset.to_ullong() 返回一个 unsigned long long 类型的值，这个类型通常是 64 位. num_bits_=0时会溢出.

测试提交流程

本地测试

  1. 创建开发环境 

    1
    2
    3
    4
    $ mkdir build
    $ cd build
    $ cmake -DCMAKE_BUILD_TYPE=Debug ..
    $ make -j`nproc`

  2. 本地测试 

    1
    2
    3
    $ cd build
    $ make -j$(nproc) hyperloglog_test
    $ ./test/hyperloglog_test

打包
  1. build目录下输入:make submit-p0,生成zip文件;
  2. 到上一层目录,执行python3 gradescope_sign.py,生成打分文件;

这里会遇到一个问题: 压缩包里的内容,正常应该是用于覆盖源文件的两个.h文件和.cpp文件(即我们写的),但压缩包里似乎并不是.

此时是build打包时出了问题,我们去看看它的Makefile,找到submit-p0对应的文件路径: 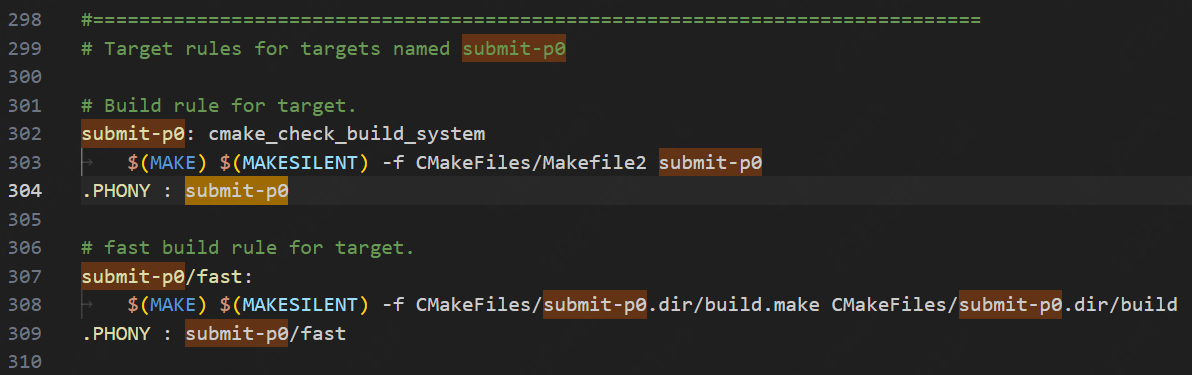去CMakeFiles/submit-p0.dir/build.make里找到真正打包的东西,改成我们想要的:

格式检查

这一步必须,否则不符合标准代码风格,提交到Gradescope也是0分: 

1
2
3
make format
make check-lint
make check-clang-tidy-p0
记出现过的报错:

变量命名(readability-identifier-naming)

根据常见的 C++ 编码规范，变量应该使用小写字母并采用下划线分隔（即蛇形命名法）. 

1
2
long double z = 0.0;  // 将 Z 修改为 z
std::bitset<OVERFLOW_BUCKET_SIZE> overflow_value(num_trailing_zeros >> 4);  // 将 overflow_value_ 修改为 overflow_value

类型名重复(modernize-use-auto)

原本使用了显式的类型名std::bitset<BITSET_CAPACITY>,而 Clang-Tidy 建议使用 auto 来简化代码,避免显式重复类型名: 

1
auto bset = std::bitset<BITSET_CAPACITY>(hash);  // 使用 auto 来推导类型

register 与关键字冲突（readability-identifier-naming）

在 C++ 中，register 是一个关键字，不能作为变量名。因此，register_ 是一个不推荐的命名方式;将其修改为 reg: 

1
2
3
4
long double z = 0.0;  // 修改 Z 为 z
for (auto &reg : registers_) {  // 修改 register_ 为 reg
    // 其他代码
}

结尾

Project#0终于完成啦!为C++的语法特性困扰了好久,呜呜呜.

不过完成是一个好的开始,继续前进!