FSDP设计解读
FSDP(Fully Sharded Data Parallelism)将AI模型的参数分片至多个数据并行的workers上,可选择性地将训练中的计算移至CPU上。每个worker上microbatch的数据是不同的。
分片(Shard):官方文档:Scaling services with Shard Manager
通常数据并行训练要求在每个GPU上,保存模型副本(引入冗余);模型并行训练在workers(GPUs)之间增添了额外的通信负担,用于同步激活值。
激活值(activations):
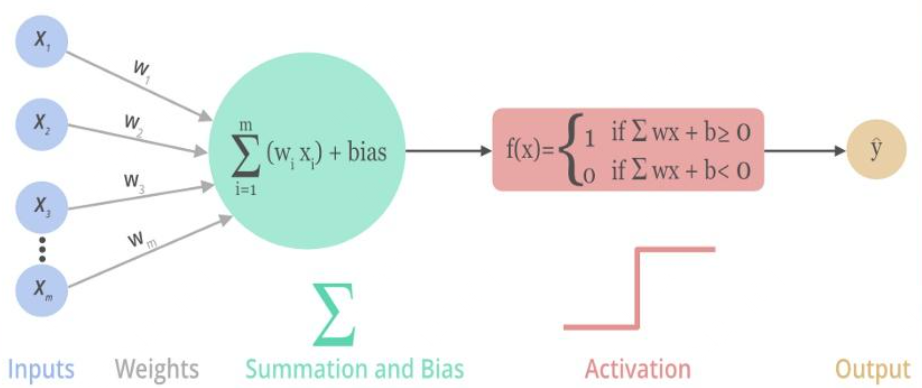
神经网络中每一层的输入输出都是一个线性求和的过程,下一层的输出只是承接了上一层输入函数的线性变换,所以如果没有激活函数,那么无论构造的神经网络多么复杂,有多少层,最后的输出都是输入的线性组合,纯粹的线性组合并不能够解决更为复杂的问题。常见的激活函数都是非线性的,因此向神经元引入非线性元素,使得神经网络可以逼近其他的任何非线性函数,这样可以使得神经网络应用到更多非线性模型中。
常见激活函数:参见Activation Functions — All You Need To Know! 1. Sigmoid函数:取值范围为(0,1),它可以将一个实数映射到(0,1)的区间,可以用来做二分类。\(f(x)=\frac{1}{1+e^{-x}}\)。不足如下: * 梯度消失:Sigmoid 函数趋近 0 和 1 的时候,Sigmoid 的梯度趋近于 0。 神经网络使用 Sigmoid 激活函数进行反向传播时,输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此,这些神经元的权重不会更新; * 不以0为中心:输出恒大于0,非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移(Bias Shift),并进一步使得梯度下降的收敛速度变慢; * 计算成本高昂:exp() 函数与其他非线性激活函数相比,计算成本高昂。
- Tanh/双曲正切函数:\(f(x)=tanh(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}\),值域为(-1,1).
- Tanh函数有梯度消失问题,但解决了不以0为中心的问题,比sigmoid函数更好。
一般的二元分类问题中,tanh用于隐藏层,sigmoid用于输出层。(并非固定,根据特定问题调整)
- ReLU函数:x>=0时,f(x)=x;x<0时,f(x)=0.即:f(x)=max(0,x) .ReLU优点如下:
- x>0时,导数为1;一定程度改善梯度消失,加速梯度下降的收敛速度;
- 计算速度加快:只存在线性关系。
不足如下: * Dead ReLU:x<0时,ReLU完全失效。在反向传播中,导致梯度为0。在训练时,如果参数在一次不恰当的更新之后,第一个隐藏层中的某个ReLU 神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活。 不以0为中心
- Leaky ReLU:
相较于ReLU的优点如下:
- Leaky ReLU 通过把 x 的非常小的线性分量给予负输入(0.01x)来调整负值的零梯度(zero gradients)问题,当 x < 0 时,它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题; leak 有助于扩大 ReLU 函数的范围,通常 a 的值为 0.01 左右; Leaky ReLU 的函数范围是(负无穷到正无穷)
- ELU:
与ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度;
- Softmax函数:用于多类分类问题。对于长度为 K 的任意实向量,Softmax 可以将其压缩为长度为 K,值在(0,1)范围内,并且向量中元素的总和为 1 的实向量。优点:
- Softmax 与正常的 max 函数不同:max 函数仅输出最大值,但 Softmax 确保较小的值具有较小的概率,并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。
- Softmax 函数的分母结合了原始输出值的所有因子,这意味着 Softmax 函数获得的各种概率彼此相关。
不足: * 在0点不可微; * 负输入的梯度为零,这意味着对于该区域的激活,权重不会在反向传播期间更新,因此会产生永不激活的死亡神经元。
- Maxout函数:任意凸函数的分段线性近似,在有限的点上是不可微的。
FSDP平衡了上述问题。它通过在GPUs上对模型参数、梯度、优化器状态分片,提升了内存效率;通过分解通信并将其与计算重合(前向/反向传播中均实现),提高计算效率。
How FSDP works
在标准的DDP(Distributed Data Parallelism)训练中,每个worker处理一个单独的batch,通过all-reduce实现梯度同步;然而,DDP中模型权重和优化器状态,在各个DDP workers中重复,带来冗余。
* Reduce-Scatter:合并梯度在不同rank上的相同blocks; * All-Gather:每个 GPU 上聚合的梯度碎片,被共享给所有 GPU。
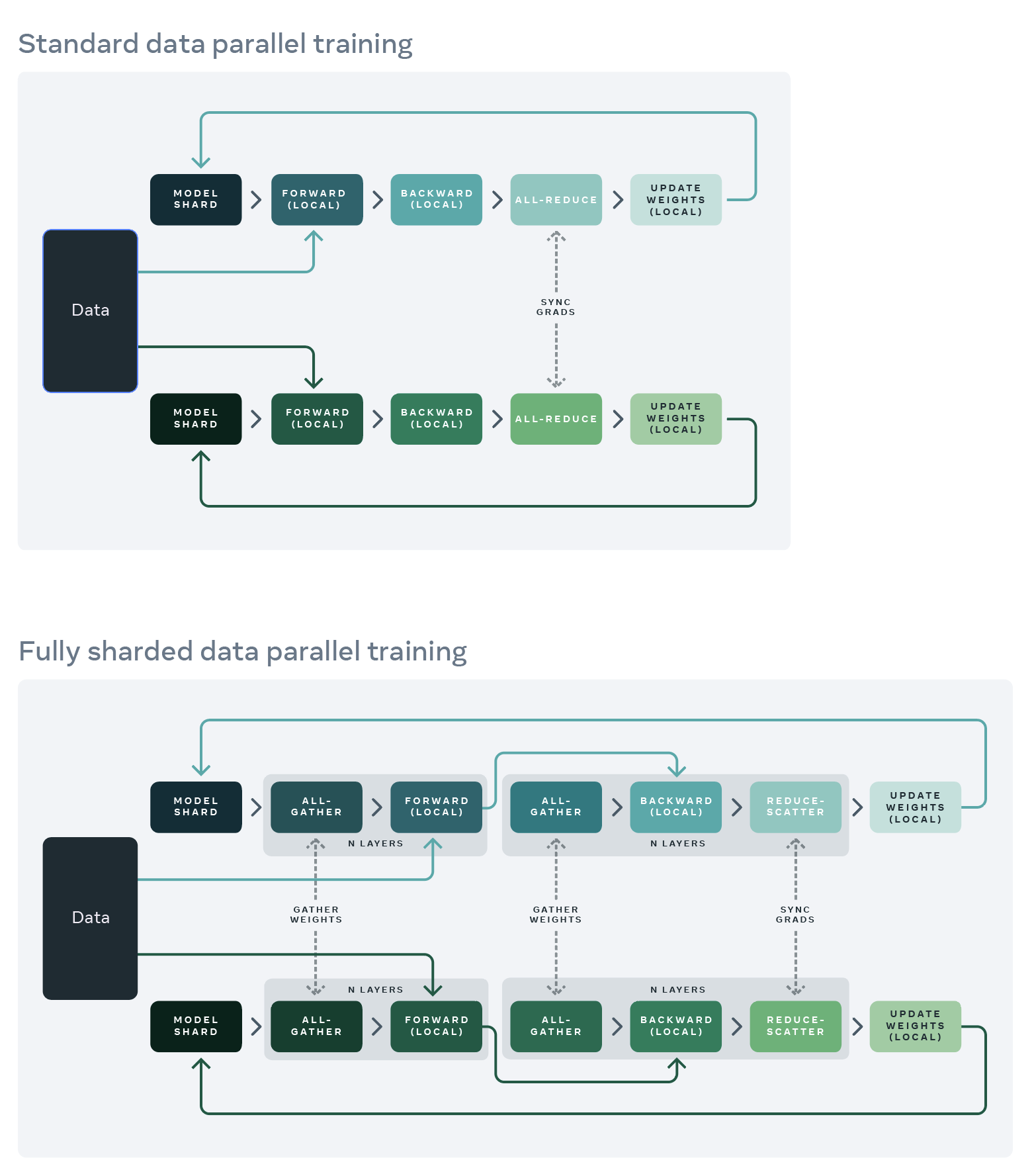
标准的DP训练 & 完全分片的DP训练:
完整的模型副本在每个GPU上保存;前向/反向传播只在一个数据分片上执行。
每个GPU完成本地计算后:每个本地进程的梯度和优化器状态,在所有GPUs上共享,以计算全局权重的更新。
每个GPU上只保存一个模型分片:
- 在前向/反向传播开始前:通过一个all-gather操作,从其他GPUs上收集权重;
- 反向传播之后:平均本地梯度,通过一个reduce-scatter操作,共享至所有GPUs,允许每个GPU更新自己的本地权重分片。
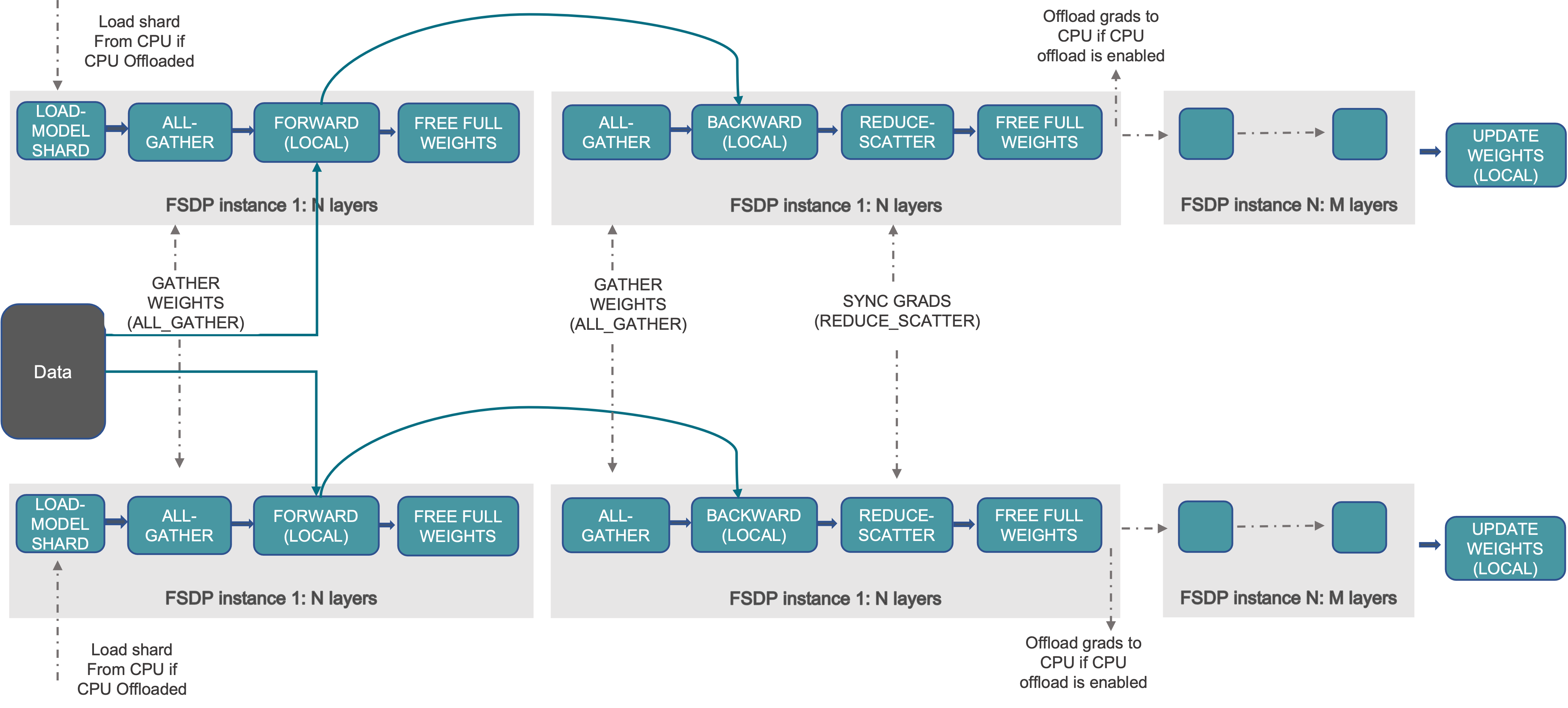
前向传播
- 对每个FSDP unit,运行all-gather收集所有rank上的模型参数切片,则每个rank上拥有当前unit的所有参数(虽然切分了模型参数,但计算时用的原始全部参数,因此FSDP依然属于数据并行);
- 执行前向传播计算;
- 每个rank上,丢掉不属于当前rank的模型参数,释放内存;
反向传播
- 对每个FSDP unit,运行all-gather收集所有rank上的模型参数切片;
- 执行反向传播计算;
- 每个rank上,丢掉不属于当前rank的模型参数,释放内存;
- 执行reduce-scatter,在不同rank之间同步梯度。
优化器更新
每个rank更新自己的局部梯度分片
一个更详细的图:
FSDP Design
PyTorch FSDP: Experiences on Scaling Fully Sharded Data Parallel
pytorch/torch/distributed/fsdp /fully_sharded_data_parallel.py
引入Sharding factor(F),取值在1~W之间(W为设备数)。 令F=W,此时采取fully sharded策略。
调用例子:
1 | # xdoctest: +SKIP("undefined variables") |
初始化
FSDP的工作过程中,前向/反向传播都以FSDP unit为规模执行,该unit即FSDP计算和通信的执行单元。这个unit是什么呢?
在源码中,FSDP采用FlatParameter类的实例,来表示一个unit,即计算和通信的基本单元。在当前设计中,FlatParameter逻辑上表示一个1D的tensor,通过n个模型参数tensor展开拼接而成(可以是sharded或unsharded)。假设unit是LlamaDecoderLayer,那么其中的所有weight,包括q_proj, k_proj, v_proj等,layernorm的所有weight全部展平拼接为一个大的1D tensor,再将这个1D tensor平均分配到每个rank。如果不能整除,先padding再切分,这样每个rank上维护一份local shard tensor。
为什么要使用1D tensor呢?主要考量通信性能的约束。包括两方面原因:
- 对于NCCL backend来说,FSDP需要调用allgather和reduce_scatter两个collective op,all_gather_into_tensor和reduce_scatter_tensor比all_gather和reduce_scatter的性能更好,而这两个op要求输入的tensor size是均等的;
- 合并和展平tensor,减少了issue collective call的次数。
如何构建1D tensor呢?提供wrap策略。
初始化FSDP module
FullyShardedDataParallel的初始化函数中调用路径如下: 1. 调用_init_param_handle_from_module初始化FSDP module的参数; 2. 在_init_param_handle_from_params中初始化FlatParamHandle实例;调用shard进行分片
分片:shard函数
- 将
FlatParameter分片:为切片后的flat parameter分配新内存;清空未分片的flat parameter的内存。
调用链:shard()->_get_shard->_get_unpadded_shard,核心的分片操作通过_get_shard()完成,而_get_shard()则依赖于_get_unpadded_shard()来获取原始的、未填充的分片。整个调用链的流程如下: 1. shard()方法被调用; 2. shard()根据是否使用分片策略来选择执行路径:如果使用分片策略,它会调用FlatParamHandle._get_shard(); 3. FlatParamHandle._get_shard()调用_get_unpadded_shard()来获取当前进程(rank)和总进程数(world_size)下的未填充分片,并计算需要填充的元素数量; 4. FlatParamHandle._get_shard()根据需要填充的元素数量对分片进行填充,并返回填充后的分片和填充的元素数量; 5. shard()方法将填充后的分片设置到flat_param中,并初始化相关的分片元数据。
1 |
|
综上所述,在FlatParamHandle._get_shard函数中,将张量分割为world_size(总进程数)个分片,并padding到相同的大小,调用_init_shard_metadata初始化当前进程分片的元数据。
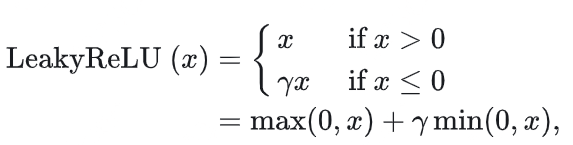 相较于ReLU的优点如下:
相较于ReLU的优点如下: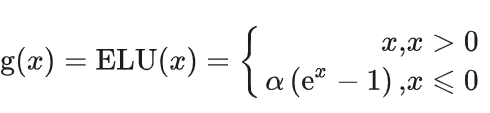 与ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度;
与ReLU 相比,ELU 有负值,这会使激活的平均值接近零。均值激活接近于零可以使学习更快,因为它们使梯度更接近自然梯度;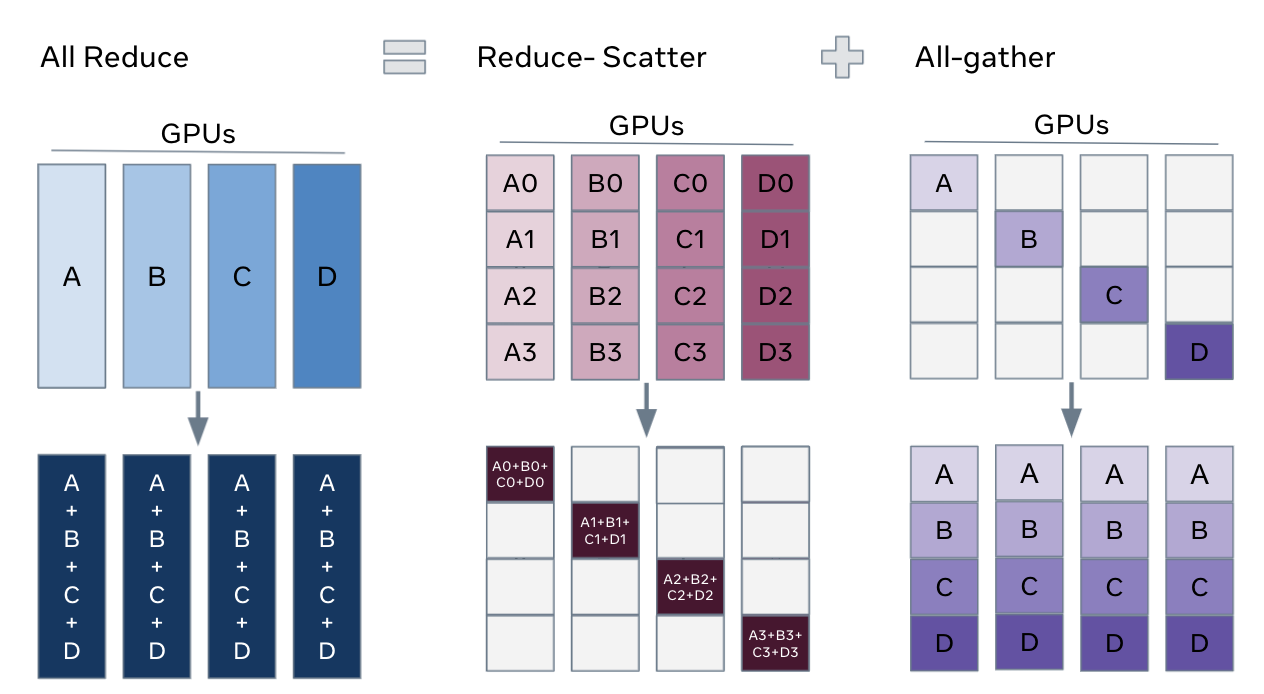 * Reduce-Scatter:合并梯度在不同rank上的相同blocks; * All-Gather:每个 GPU 上聚合的梯度碎片,被共享给所有 GPU。
* Reduce-Scatter:合并梯度在不同rank上的相同blocks; * All-Gather:每个 GPU 上聚合的梯度碎片,被共享给所有 GPU。