并行训练系列：7. Flash Attention V1/V2

对于输入序列长度为$N$的 Transformer 类模型，其计算复杂度和存储空间为$O(N^2)$；Flash Attention（Fast and Memory Efficient Exact Attention with IO-Awareness）技术旨在缓解上述计算和存储压力。

一个洞察为：计算慢的卡点在于读写速度，而非计算能力。Flash Attention 通过 tiling 和 kernel fusion 降低对显存（HBM）的访问次数以加速计算。

计算瓶颈分析：
定义：
$\pi$：硬件算力上限。每秒钟能完成的浮点运算次数，单位是 FLOPS 或 FLOP/s；
$\beta$：硬件带宽上限。每秒能完成的内存交换次数，单位是 Byte/s；
$\pi_t$：算法所需的总计算量；$\beta_t$：算法所需的总数据读取存储量。
算法的计算时间：$T_{cal}=\frac{\pi_t}{\pi}$；算法的数据读取时间：$T_{load}=\frac{\beta_t}{\beta}$
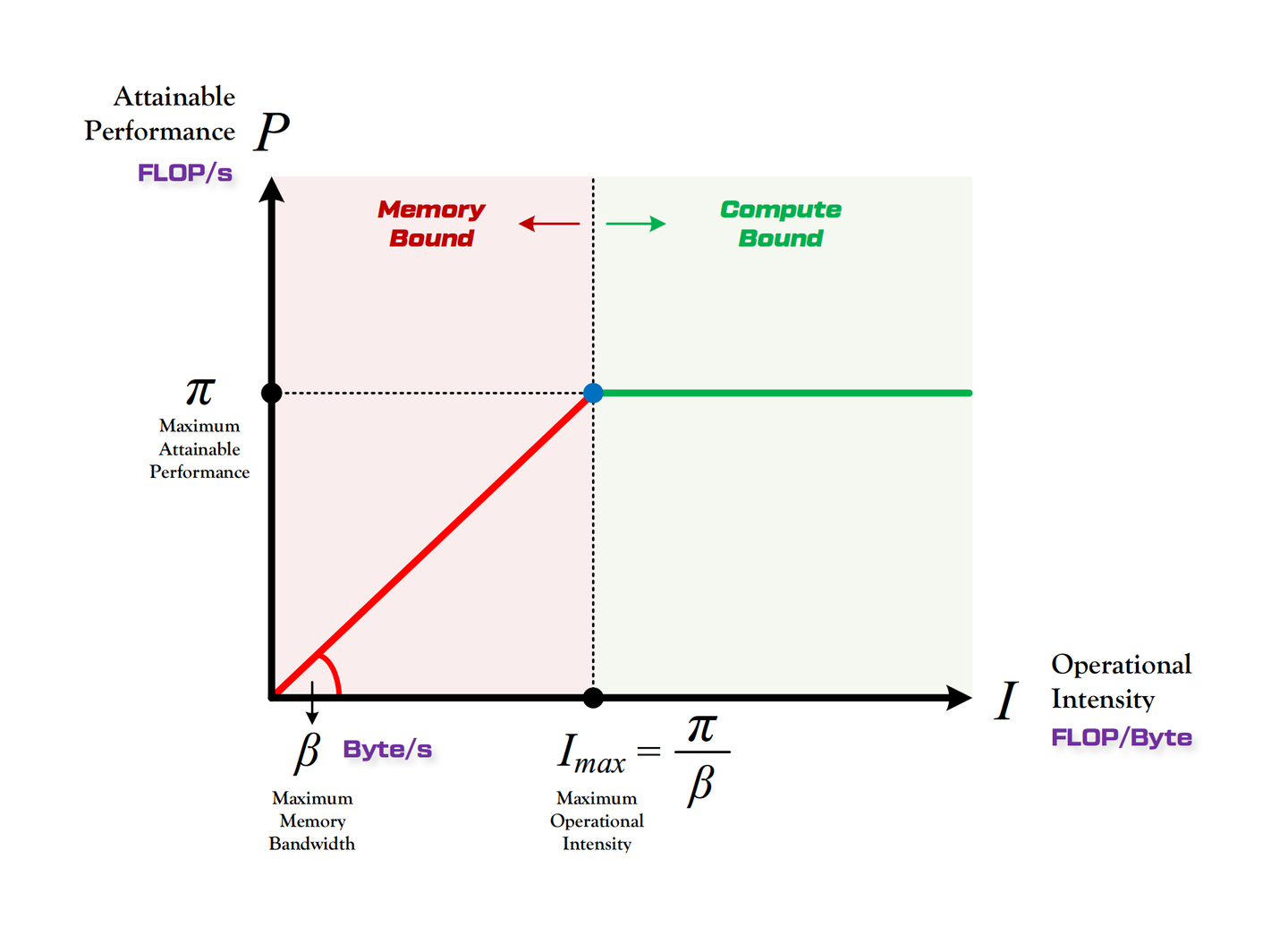
计算限制：$T_{cal}>T_{load}$；内存限制：$T_{cal}<T_{load}$
大矩阵乘法通常受计算限制；逐点运算操作（激活函数、dropout、mask、softmax、normalization 等）受内存限制。
假设矩阵$Q, K\in\mathbb{R}^{N\times d}$，其中$N$为序列长度，$d$为 embedding dim；标准注意力的计算公式为：
\[ O=softmax(\frac{1}{\sqrt{d}}QK^T)V=softmax(S)V=PV \]
计算量：计算$S=QK^T\in R^{N\times N}$，$O=PV\in R^{N\times d}$.
数据读取量：
第1步对$Q, K$的读取共2次，第3步对$S$的写入1次；
第4步对$S$的读取1次，第7步对$P$的写入1次；
第8步对$P, V$的读取共2次，第10步对$O$的写入1次。
$\frac{\pi_t}{\beta_t}=\frac{4N^2d}{2Nd+2Nd+4N^2}=\frac{N^2d}{Nd+N^2}$
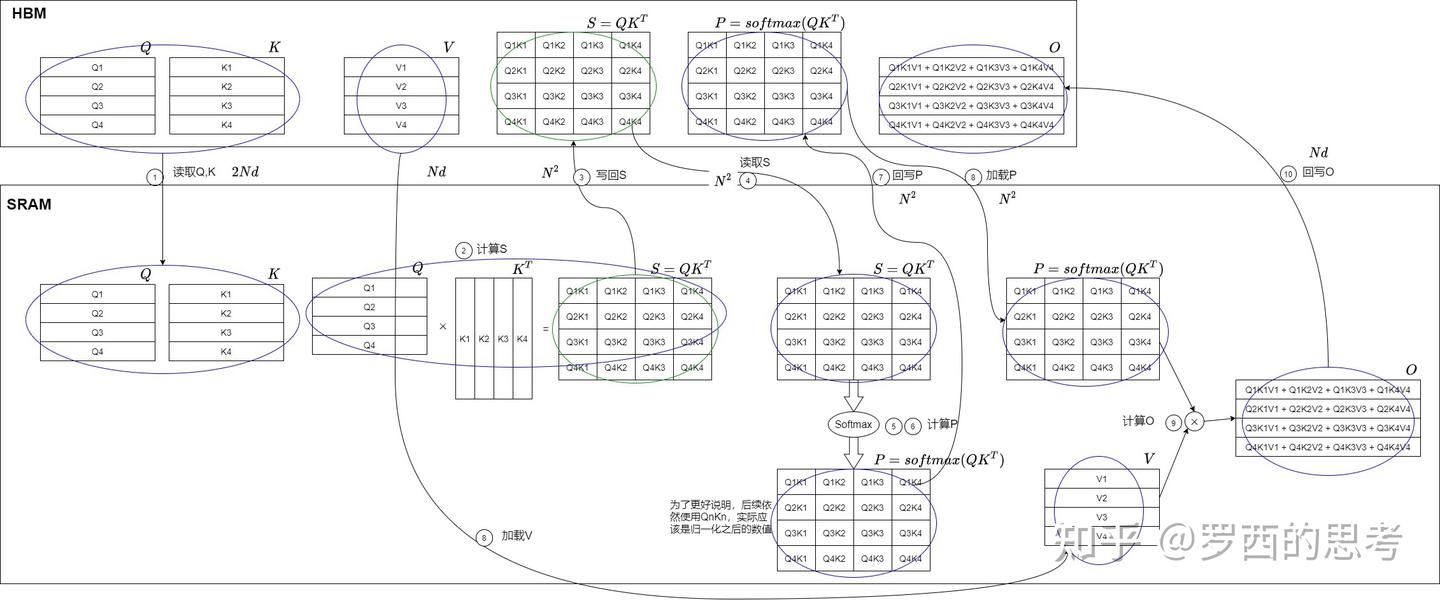
标准注意力在 SRAM 和 HBM 之间的交互流程如下：

GPU 的计算流程是：将数据从显存（HBM）加载至 on-chip 的 SRAM 中，由 SM 读取并计算；计算结果通过 SRAM 返回给 HBM。最节省内存的做法是：以 SRAM 的存储为上限，尽可能每次加载时打满，目标是减少 HBM 和 SRAM 之间的换入换出。

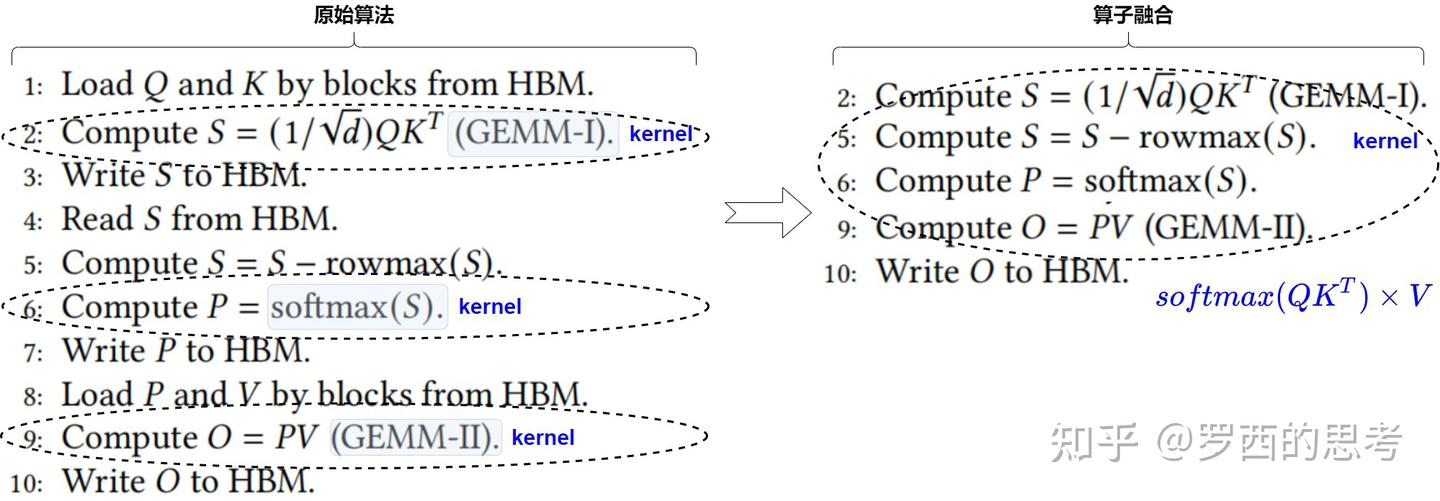
标准注意力机制$softmax(\frac{QK^T}{\sqrt{d_k}}\times V)$主要分为3个步骤，分别对应依次执行的3个 kernel：**gemm（q⁢u⁢e⁢r⁢y×k⁢e⁢y）、point-wise的softmax、gemm（a⁢t⁢t⁢n⁢_⁢s⁢c⁢o⁢r⁢e×v⁢a⁢l⁢u⁢e）**。Flash Attention 的方案是：以两个 gemm kernel 为中心进行融合，使用 SRAM 存储中间结果（不写回 HBM）；通过分块解决无法容纳整个中间矩阵的问题。

整体流程如下：

Flash Attention V1

Tiling

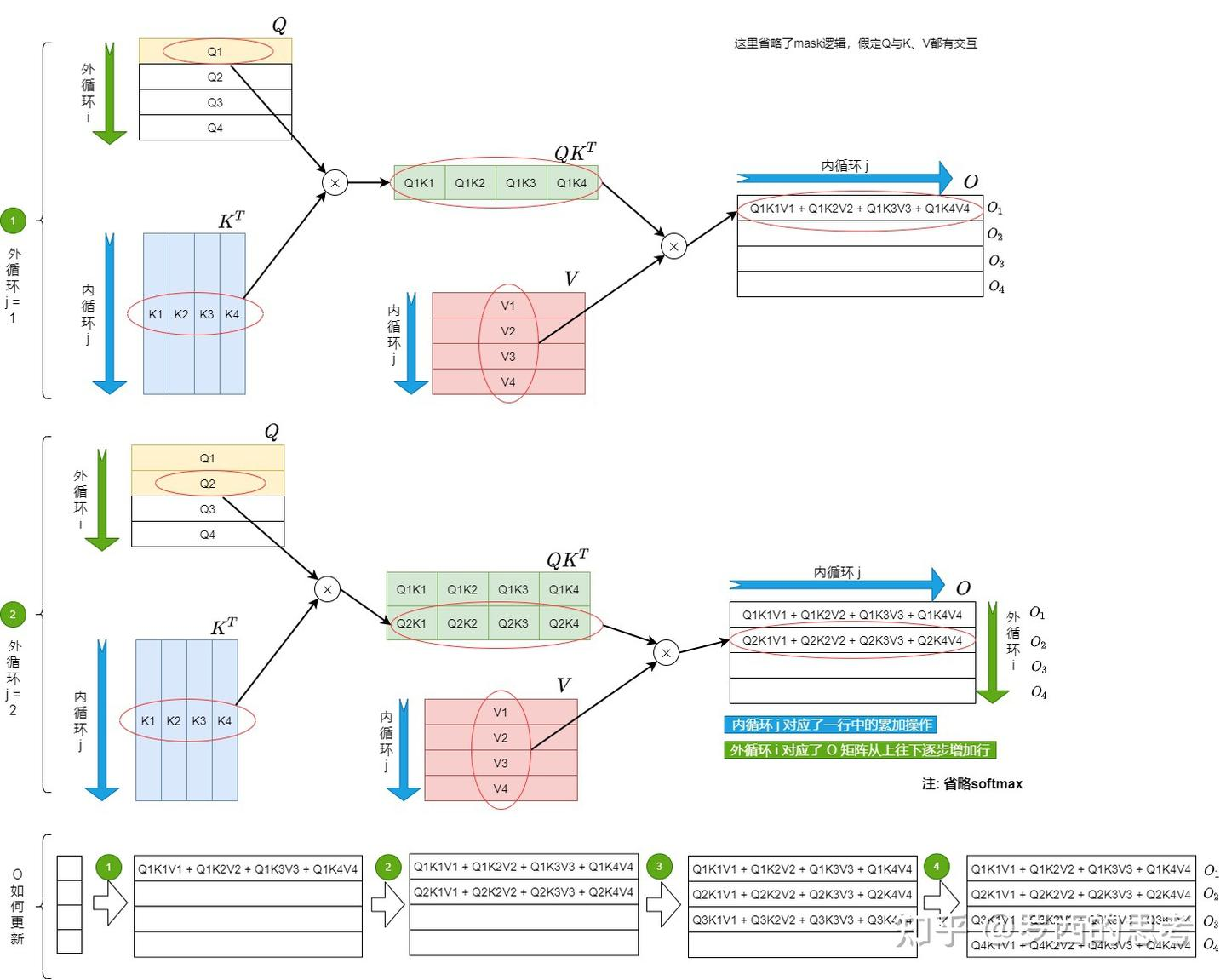
将$K, V$切分成$T_c$个小块，将$Q, O$切分成$T_r$个小块，执行双层循环计算：

O_0 = 0
for 1 <= j <= Tc: # K, V 外循环
    load V_j, K_j
    for 1 <= i <= Tr: # Q, O 内循环
        load O_i^{j-1}, Q_i
        S = softmax(Q_i * K_j^T) # 计算得 S
        O_i^j = S * V_j # 得到 O_i 行的第 j 列
        O_i = O_i^j + O_i^{j-1} # 完成 O_i 的一次累加更新
        store O_i # 回写

HBM 和 SRAM 之间的数据读取/写入操作如下：

Safe Softmax 动态更新

朴素的 softmax 计算：$softmax(x_i)=\frac{e^{x_i}}{\sum_{j=1}^B e^{x_j}}$ 容易出现上溢和下溢问题。（指数项$e^{x_i}$超过浮点数表示范围时发生上溢；$x_i$是较大的负值时每个$e^{x_i}$下溢导致分母为0）

稳定的 softmax 版本：

\[ \begin{align*} m(x)&=\max([x_1, x_2, ..., x_B]) \\ f(x)&=[e^{x_1-m(x)}, ..., e^{x_B-m(x)}] \\ softmax(x)&=\frac{f(x)}{\sum_i f(x)_i} \end{align*} \]

其中，$\sum_i f(x)_i$ 是$f(x)$的所有元素求和。

softmax 分块计算是一大难点，因为其分母依赖于每一个元素。分块计算的关键在于更新全局最大值$m(x)$和分母$\sum_i f(x)_i$.

考虑向量$x\in\mathbb{R}^{2B}$，分成两块：$x=[x^{(1)}, x^{(2)}]$。在分块计算中先处理$x^{(1)}$，再处理$x^{(2)}$.有：

\[ \begin{align*} m(x^{(1)})&=\max([x_1^{(1)}, x_2^{(1)}, ..., x_B^{(1)}]) \\ f(x^{(1)})&=[e^{x_1^{(1)}-m(x^{(1)})}, ..., e^{x_B^{(1)}-m(x^{(1)})}] \\ softmax(x^{(1)})&=\frac{f(x^{(1)})}{\sum_i f(x^{(1)})_i} \end{align*} \]

以上是$x^{(1)}$对应的局部计算结果，不保存 $x^{(1)}$，选择保存 $m(x^{(1)})$ 和 $l(x^{(1)})$，用于在处理完 $x^{(2)}$ 后更新 $x^{(1)}$.

保存两个全局标量：当前最大值 $m_{max}$ 和全局 exp 求和项 $l_{all}$. 当前：$m_{max}=m(x^{(1)}), l_{all}=l(x^{(1)})$.

采取同样的流程处理$x^{(2)}$.全局标量更新方法如下：

\[ \begin{align*} m_{max}^{new}&=\max([m_{max}, m(x^{(2)})]) \\ l_{all}^{new}&=e^{m_{max}-m_{max}^{new}}l_{all}+e^{m(x^{(2)})-m_{max}^{new}}l(x^{(2)}) \end{align*} \]

分块计算时，局部的$f(x^{(2)})=[e^{x_1^{(2)}-m(x^{(2)})}, ..., e^{x_B^{(2)}-m(x^{(2)})}]$，则全局的$f^{new}(x^{(2)})$更新为：

\[ \begin{align*} f^{new}(x^{(2)})&=f(x^{(2)})·e^{m(x^{(2)})-m_{max}^{new}} \\ &=[e^{x_1^{(2)}-m_{max}^{new}}, ..., e^{x_B^{(2)}-m_{max}^{new}}] \end{align*} \]

更新 $softmax(x^{(2)})$ 的分子部分：

\[ \begin{align*} softmax^{temp}(x^{(2)})&=softmax(x^{(2)})·e^{m(x^{(2)})-m_{max}^{new}} \\ &=\frac{f(x^{(2)})}{l(x^{(2)})}·e^{m(x^{(2)})-m_{max}^{new}} \\ &=\frac{f^{new}(x^{(2)})}{l(x^{(2)})} \end{align*} \]

将分母 $l(x^{(2)})$ 替换为全局 exp 求和项 $l_{all}^{new}$，即：

\[ \begin{align*} softmax^{new}(x^{(2)})&=softmax^{temp}(x^{(2)})·\frac{l(x^{(2)})}{l_{all}^{new}} \\ &=\frac{f^{new}(x^{(2)})}{l_{all}^{new}} \end{align*} \]

整合后观察 $softmax(x^{(2)})$ 到 $softmax^{new}(x^{(2)})$ 的更新方式：

\[ softmax^{new}(x^{(2)})=\frac{softmax(x^{(2)})·l(x^{(2)})·e^{m(x^{(2)})-m_{max}^{new}}}{l_{all}^{new}} \]

用到以下额外保存的量：

$x^{(2)}$ 的局部 softmax 值 $softmax(x^{(2)})$；
$x^{(2)}$ 的局部 exp 求和项 $l(x^{(2)})$；
$x^{(2)}$ 的局部最大值 $m(x^{(2)})$；
全局最大值 $m_{max}^{new}$；
全局 exp 求和项 $l_{all}^{new}$.

注意，以上从局部到全局的更新无需 $x^{(1)}$ 或 $x^{(2)}$ 的整个向量值。

Forward Pass

如上图所示：

根据 SRAM 的大小$M$选择合适的分块大小$B_c, B_r$；
在 HBM 中初始化若干变量，包括：最终输出$O$，指数求和项$l$，每行 Attention Score 的最大值$m$；
将 $Q\in\mathbb{R}^{N\times d}$ 沿着行切分为 $T_r$ 个大小为 $B_r\times d$ 的小块；将 $K, V\in\mathbb{R}^{N\times d}$ 沿着行切分为 $T_c$ 个大小为 $B_c\times d$ 的小块。
将 $O\in\mathbb{R}^{N\times d}, m, l\in\mathbb{R}^{N}$ 沿着行切分为 $T_r$ 个小块。
外循环：遍历$K, V$，由 $T_c$ 控制；
当前外循环遍历到的$K_j, V_j$由 HBM 读入 SRAM；
内循环：遍历$Q, O, l, m$，由 $T_r$ 控制；
当前内循环遍历到的$Q_i, O_i, l_i, m_i$由 HBM 读入 SRAM；
计算当前分块的 Attention Score：$S_{ij}=Q_iK_j^{T}\in\mathbb{R}^{B_r\times B_c}$；
对于分块的 Attention Score $S_{ij}$，计算其每一行的最大值 $\tilde{m_{ij}}\in\mathbb{R^{B_r}}$；
- 基于 $\tilde{m_{ij}}$，计算指数项 $\tilde{P_{ij}}=\exp(S_{ij}-\tilde{m_{ij}})\in\mathbb{R}^{B_r\times B_c}$；
- 基于 $\tilde{P_{ij}}$，计算 exp 求和项 $rowsum(\tilde{P_{ij}})\in\mathbb{R^{B_r}}$.
计算当前的全局量 $m_i^{new}$ 和 $l_i^{new}$（此时暂且不用于更新旧的 $m_i$ 和 $l_i$，因为还需要参与后续计算）
softmax 计算时，行与行之间无交互，分块是列意义上的。因此暂不考虑 batch 计算，每个小块简化为 $S_{ij}\in\mathbb{R}^{1\times B_c}$. 使用 $S_i$ 表示每一行的 Attention Score，$SM_i$ 表示每一行的 softmax.
1. 处理 $S_{11}$；
2. 处理 $S_{12}$：计算 $S_{12}$ 的局部 softmax；$SM_1$ 更新为 $SM_1=SM_1^{new}+SM_{12}=\frac{SM_1·l_1·e^{m_1-m_1^{new}}}{l_1^{new}}+\frac{\tilde{P_{12}}·e^{m_{12}-m_1^{new}}}{l_1^{new}}$
  等式右侧第一项是一个$N$维向量，前$B_c$项有效，其他均为0；第二项中 $\tilde{P_{12}}\in\mathbb{R}^{1\times B_c}$，可以重定义为一个$N$维向量，其他位置上均为0.
  求和效果等价于：更新第$[1, B_c]$列的值；将新值写入第$[B_c+1, 2B_c]$列.
3. 更新完 $SM_1$ 后，输出 $O_1$ 更新为 $O_1=O_1^{new}+O_{12}=\frac{O_1·l_1·e^{m_1-m_1^{new}}}{l_1^{new}}+\frac{\tilde{P_{12}}·e^{m_{12}-m_1^{new}}}{l_1^{new}}·V_2$.（$V_2$ 对应的是 $S_{12}$ 中的列数）
更新 $l_i$ 和 $m_i$.

$B_r, B_c$ 的设置：$B_c=\lceil\frac{M}{4d}\rceil$，$B_r=min(\lceil\frac{M}{4d}\rceil, d)$.
假设 $B_c=B_r=\frac{M}{4d}$，则从 HBM 加载到 SRAM 的4个矩阵 $K_j, V_j, O_i, Q_i$ 的尺寸均为 $[\frac{M}{4d}, d]$.因此数据读取的总开销等于 SRAM 的大小 $M$（$l_i, m_i$ 可忽略不计）.

Backward Pass

Softmax 求偏导：
softmax 函数表达式为：$y_i=\frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}$
求偏导有：$\frac{\partial y_i}{\partial z_j}=\frac{\partial \frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}}{\partial z_j}$
当 $i=j$ 时，有 $\frac{\partial e^{z_i}}{\partial z_j}=e^{z_i}$，则：
\[ \begin{align*} \frac{\partial y_i}{\partial z_j}&=\frac{\partial \frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}}{\partial z_j} \\ &=\frac{e^{z_i}·\sum_{t=1}^me^{z_t}-e^{z_i}·e^{z_j}}{(\sum_{t=1}^me^{z_t})^2} \\ &=\frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}-\frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}·\frac{e^{z_j}}{\sum_{t=1}^me^{z_t}} \\ &=y_i(1-y_j) \end{align*} \]
2. 当 $i\neq j$ 时，有 $\frac{\partial e^{z_i}}{\partial z_j}=0$，则：
\[ \begin{align*} \frac{\partial y_i}{\partial z_j}&=\frac{\partial \frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}}{\partial z_j} \\ &=\frac{0·\sum_{t=1}^me^{z_t}-e^{z_i}·e^{z_j}}{(\sum_{t=1}^me^{z_t})^2} \\ &=-\frac{e^{z_i}}{\sum_{t=1}^me^{z_t}}·\frac{e^{z_j}}{\sum_{t=1}^me^{z_t}} \\ &=-y_i y_j \end{align*} \]
$y=softmax(z)$ 关于 $z$ 的求导结果是一个 Jacobian 矩阵 $diag(y)-y^Ty$：
\[ \begin{align*} \frac{\partial\vec{y}}{\partial\vec{z}}&=diag(\vec{y})-\vec{y}^T\vec{y} \\ &=\begin{bmatrix}y_1 & 0 & 0 \\0 & y_2 & 0 \\0 & 0 & y_3\end{bmatrix}-\begin{bmatrix}y_1 \\y_2 \\y_3\end{bmatrix}\begin{bmatrix}y_1 & y_2 & y_3 \end{bmatrix} \\ &=\begin{bmatrix}y_1-y_1^2 & -y_1y_2 & -y_1y_3 \\-y_2y_1 & y_2-y_2^2 & -y_2y_3 \\-y_3y_1 & -y_3y_2 & y_3-y_3^2\end{bmatrix} \end{align*} \]
记 $\frac{\partial L}{\partial y}=[dy_1, dy_2, dy_3]$，有：
\[ \begin{align*} \frac{\partial L}{\partial\vec{z}}&=\frac{\partial L}{\partial\vec{y}}\frac{\partial\vec{y}}{\partial\vec{z}}=d\vec{y}(diag(\vec{y})-\vec{y}^T\vec{y}) \\ &=[dy_1, dy_2, dy_3]\begin{bmatrix}y_1-y_1^2 & -y_1y_2 & -y_1y_3 \\-y_2y_1 & y_2-y_2^2 & -y_2y_3 \\-y_3y_1 & -y_3y_2 & y_3-y_3^2\end{bmatrix} \end{align*} \]

forward 过程中，没有保存 $S$ 和 $P$ 这两个中间结果，而是保存 $m$ 和 $l$，用于 backward 阶段中重新计算出 $S$ 和 $P$.

流程如下：

计算量和显存需求

计算量：主要关注矩阵乘法。

第9行：$S_{ij}=Q_iK_j^T\in\mathbb{R}^{B_r\times B_c}$，其中 $Q_i\in\mathbb{R}^{B_r\times d}, K_j\in\mathbb{R}^{d\times B_c}$，则 $S_{ij}$ 的计算量为 $O({B_r B_c d})$；
第12行：$\tilde{P_{ij}}V_j$，其中 $\tilde{P_{ij}}\in\mathbb{R}^{B_r\times B_c}, V_j\in\mathbb{R}^{B_c\times d}$，计算量为 $O({B_r B_c d})$.
执行的循环次数：$T_cT_r=\frac{N}{B_c}\frac{N}{B_r}$

因此，Flash Attention V1 的 forward 总计算量为：$O(\frac{N^2}{B_cB_r}B_rB_cd)=O(N^2d)$

标准 Attention 的需要存储 $S, P$，显存需求为 $O(N^2)$；Flash Attention 只存储 $m, l$，$S, P$ 在 backward 中重计算，显存需求降低至 $O(N)$.

IO 复杂度

标准 Attention 的总开销为 $4Nd+4N^2$，IO 复杂度为 $O(Nd+N^2)$；

Flash Attention V1：

第6行：每个外循环加载 $K, V$ 的一小块，所有外循环一共加载一次完整的 $K, V\in\mathbb{R}^{N\times d}$，IO 复杂度为 $O(Nd)$；
第8行：每个内循环加载 $Q, O, m, l$ 的一小块，一个外循环中的所有内循环共加载一次完整的 $Q, O\in\mathbb{R}^{N\times d}$（$m, l$ IO 复杂度为 $O(N)$，忽略不计），一共有 $T_c$ 次外循环。总 IO 复杂度为 $O(T_cNd)$.
第12/13行：将$O, m, l$ 写回 HBM，IO 复杂度为 $O(Nd)$.

综上，Flash Attention V1 的 forward 总 IO 时间复杂度为：$O(T_cNd)=O(\frac{N}{B_c}Nd)=O(\frac{4Nd}{M}Nd)=O(\frac{N^2d^2}{M})$.

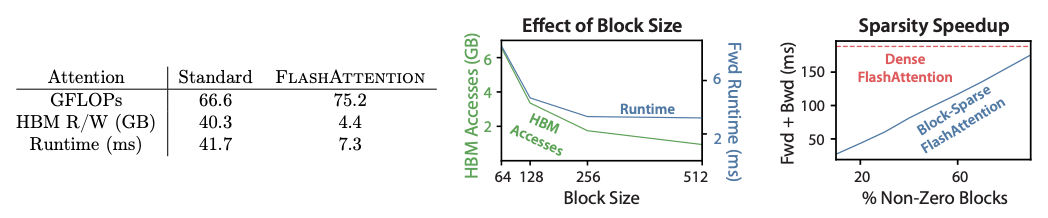
论文中有述，一般 $d$ 的取值为 64～128，$M$ 的取值为 100KB 左右，因此有 $\frac{d^2}{M}<<1$。

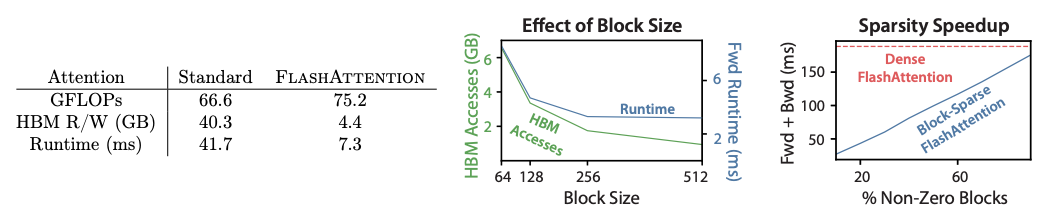
从中间的图可知：数据块越大，读写次数越少，runtime 整体下降（IO 复杂度为 $O(T_cNd)$，数据块越大，$O(T_c)$ 越小）；数据块大小>256 后，runtime 下降不明显，因为随着矩阵扩大，计算耗时增加，抵消 IO 复杂度降低节省的时间。

Flash Attention V2

FlashAttention V2 相对 V1 主要有3个优化点：Algorithm、Parallelism 和 Work Partitioning。

Algorithm

观察 Flash Attention V1 的 softmax 更新公式：

\[ \begin{align*} softmax^{new}(x^{(2)})&=softmax^{temp}(x^{(2)})·\frac{l(x^{(2)})}{l_{all}^{new}} \\ &=\frac{f^{new}(x^{(2)})}{l(x^{(2)})}·\frac{l(x^{(2)})}{l_{all}^{new}} \\ &=\frac{f^{new}(x^{(2)})}{l_{all}^{new}} \end{align*} \]

以上全局更新的关键点是：将局部的 exp 求和项 $l(x^{(2)})$ 替换为全局的 exp 求和项 $l_{all}^{new}$.

计算 $softmax^{new}(x^{(3)})$ 时，需要乘此时的 $l(x^{(3)})$（对应上一轮的 $l_{all}^{new}$），再除以新的全局 exp 求和项。

每遍历到一个分块，都会做一次类似的更新操作。实际上等价于：在最后除以最新的 $l_{all}^{new}$.

举个栗子（今天北京初雪，想吃糖炒板栗）：
对于一个等差数列：1, 2, 3, ...；Flash Attention V1 的计算方法为：
$N=2: f=\frac{1+2}{2}=1.5$
$N=3: f=\frac{1.5\times 2+3}{3}=2$
每一次都算出前 $N$ 个数的平均值；第 $N+1$ 步更新平均值。
Flash Attention V2 的做法优化为：
$N=2: f=1+2=3$
$N=3: f=3+3=6$
最后再除以 $N$.

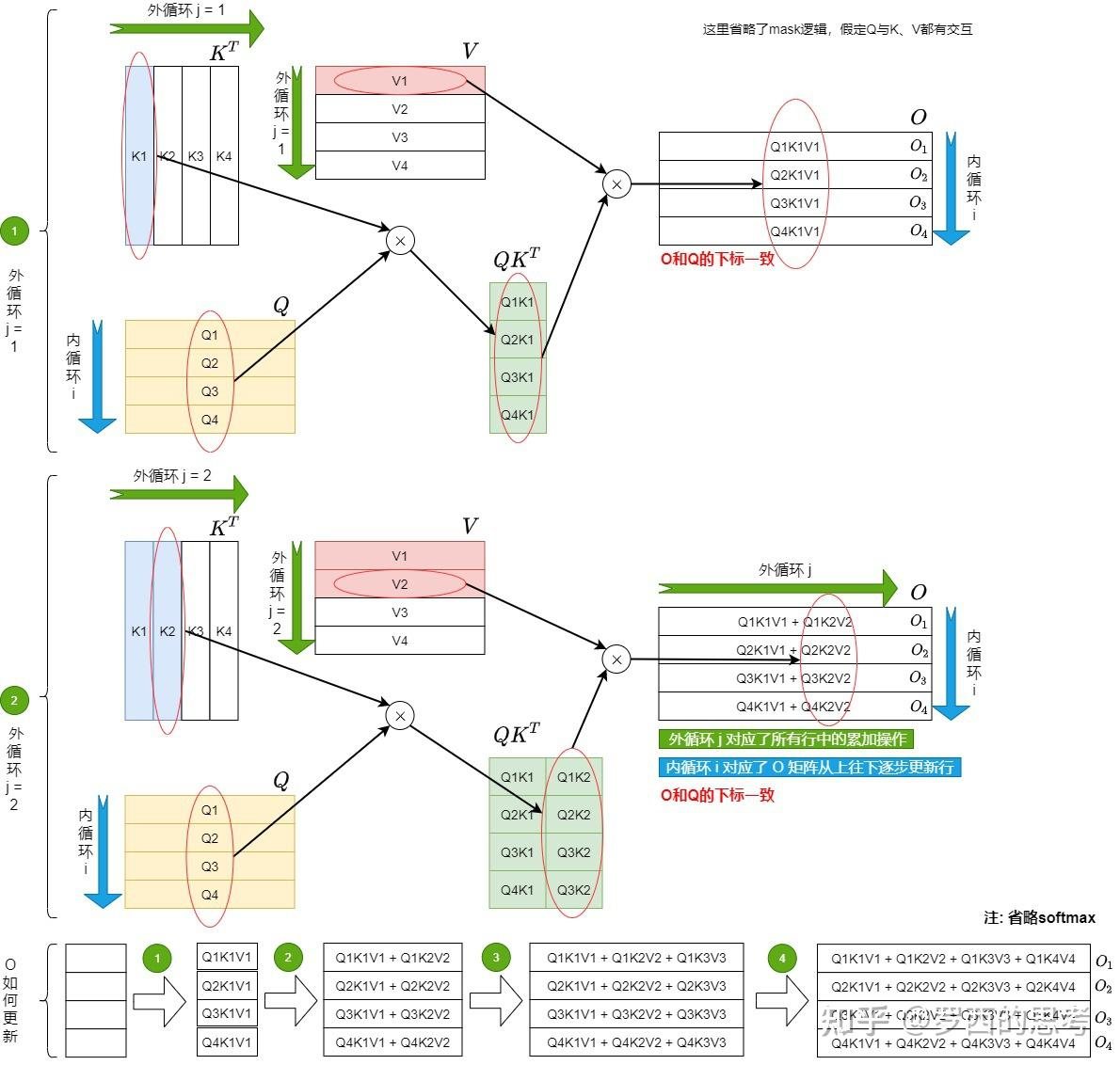
从 DataFlow 的维度上看：V1 的方案是外层循环加载 $K, V$，内层循环加载 $Q$，那么内层循环每次计算的是 $O_i$ 的一部分，对于同一个 $Q_i$，不同的 $K_j, V_j$ 都需要读写一次 $O_i$，带来频繁读写 HBM 的问题。

$O_i$ 的更新与 $Q_i$ 严格绑定，而不同 $Q_i$ 的 Attention Score 的计算是完全独立的。所以 V2 的做法是：以 $Q$ 作为外循环，$K, V$ 作为内循环。每一个外循环中，完成 $O_i$ 的计算，即每个 $O_i$ 只需要读写一次。

计算流程如下：

HBM 和 SRAM 之间的 IO 操作如下：

Forward Pass

如上图所示：

将 $Q\in\mathbb{R}^{N\times d}$ 沿着行切分为 $T_r$ 个大小为 $B_r\times d$ 的小块；将 $K, V\in\mathbb{R}^{N\times d}$ 沿着行切分为 $T_c$ 个大小为 $B_c\times d$ 的小块。
将 $O\in\mathbb{R}^{N\times d}, m, l\in\mathbb{R}^{N}$ 沿着行切分为 $T_r$ 个小块。
外循环：遍历$Q, O, l, m$，由 $T_r$ 控制；
当前外循环遍历到的 $Q_i$ 由 HBM 读入 SRAM；
初始化 $O_i\in\mathbb{R}^{B_r\times d}, l_i, m_i\in\mathbb{R}^{B_r}$；
内循环：遍历$K, V$，由 $T_c$ 控制；
当前内循环遍历到的 $K_j, V_j$ 由 HBM 读入 SRAM；
计算当前分块的 Attention Score：$S_{i}^{(j)}=Q_iK_j^{T}\in\mathbb{R}^{B_r\times B_c}$；
对于分块的 Attention Score $S_{i}^{(j)}$，计算其截止到当前分块（包含当前分块）的 rowmax $\in\mathbb{R^{B_r}}$；
- 基于 $m_{i}^{(j)}$，计算指数项 $\tilde{P_{i}^{(j)}}=\exp(S_{i}^{(j)}-m_{i}^{(j)})\in\mathbb{R}^{B_r\times B_c}$；
- 基于 $\tilde{P_{i}^{(j)}}$，计算截止到当前分块（包含当前分块）的 rowsum $l_{i}^{(j)}\in\mathbb{R^{B_r}}$.
遍历完所有 $K, V$ 之后，得到的 $O_i^{(j)}$ 等于最终的全局结果。

与 V1 相比，V2 不用在 FWD 中存储每一个 $Q_i$ 对应的中间结果 $m_i, l_i$；然而依然需要在 BWD 中使用 $m_i, l_i$ 完成 $S_i^{(j)}, P_i^{(j)}$ 的重计算。V2 采用一个替代方式：存储 $L_i=m_i^{(T_c)}+\log(l_i^{(T_c)})$（这里的 $m_i, l_i$ 分别对应全局的 rowmax 和 rowsum.

$B_r, B_c$ 的设置：$B_c=\lceil\frac{M}{4d}\rceil$，$B_r=min(\lceil\frac{M}{4d}\rceil, d)$.
假设 $B_c=B_r=\frac{M}{4d}$，则从 HBM 加载到 SRAM 的4个矩阵 $K_j, V_j, O_i, Q_i$ 的尺寸均为 $[\frac{M}{4d}, d]$.因此数据读取的总开销等于 SRAM 的大小 $M$（$l_i, m_i$ 可忽略不计）.

Backward Pass

V2 的 BWD 的内外循环依然采用：$K, V$ 外循环，$Q$ 内循环。因为在 BWD 的关键步骤是：$dK_j, dV_j, dQ_i$（$dK_j, dV_j$ 沿着 $i$ 方向 all-reduce；$Q_i$ 沿着 $j$ 方向 all-reduce.）；简化的是外循环的计算。因此将 $K, V$ 放在外循环简化最多。

重计算 $P_i^{(j)}=diag(l_i^{(j)})^{-1}\exp(S_i^{(j)}-m_i^{(j)})=\exp(S_i^{(j)}-m_i^{(j)}-\log(l_i^{(j)})=\exp(S_i^{(j)}-L_i))$，其中：$L_i=m_i^{(T_c)}+\log(l_i^{(T_c)})$.

这是在 FWD 中存储 $L_i$ 的意义。

Parallelism

优化 Attention 部分 thread blocks 的并行化计算，新增 seq_len 维度的并行，使得 SM 的利用率尽量打满。

相较于 CPU，GPU 更适合并行计算。
Thread Block：在每个 thread block 中包含多个 wrap，每个 wrap 包含 32 个 threads；同一个 wrap 中的所有 threads 协作完成矩阵乘法，同一个 thread block 中的所有 wraps 共享存储空间。
Streaming multiprocessors（SM）是 GPU 中真正的物理计算单元，thread blocks 最终被调度至 SM 上计算。因此并行化的最终目标是打满 SM。

// gridDim in V1
// params.b = batch_size, params.h = num_heads
dim3 grid(params.b, params.h);

// gridDim in V2
const int num_m_block = (params.seqlen_q + Kernel_traits::kBlockM - 1) / Kernel_traits::kBlockM;
dim3 grid(num_m_block, params.b, params.h);

V1 在 batch 内部、同一个 attention block 的 heads 之间实现并行计算（每个 attention head 对应一个 thread block）；block 将被调度至 SM 上执行。以 A100 GPU 为例（一共有 108 个 SM）：如果 block 数量较多（比如 80 个以上），说明 SM 利用率较高；然而，随着 LLM 的上下文窗口变长（即 seq_len 变长），单卡上的 batch_size 和 num_heads 将随之变小，导致较多的 SM 空转。

在 V2 的 cutlass 实现中，对 $Q$ 的 seq_len 进行切分：FWD 中 $Q$ 为外循环，$K, V$ 为内循环，不同 $Q_i$ 之间的计算是独立的，因此可以并行。

V1 后期也引入了基于 $Q$ 的 sequence parallel，grid 形式为 (batch_size, num_heads, num_m_blocks)；V2 中的 grid 形式调整为 (num_m_blocks, batch_size, num_heads).
这一改进的目的为：提升L2 cache hit rate。将 num_m_blocks 放在最外层循环，那么同一列的 block 会相邻；对于同一列的 block，读取的是相同的 $K_j, V_j$（可以直接从 Cache 中取）

上图为 V2 的 FWD/BWD 过程中的并行。

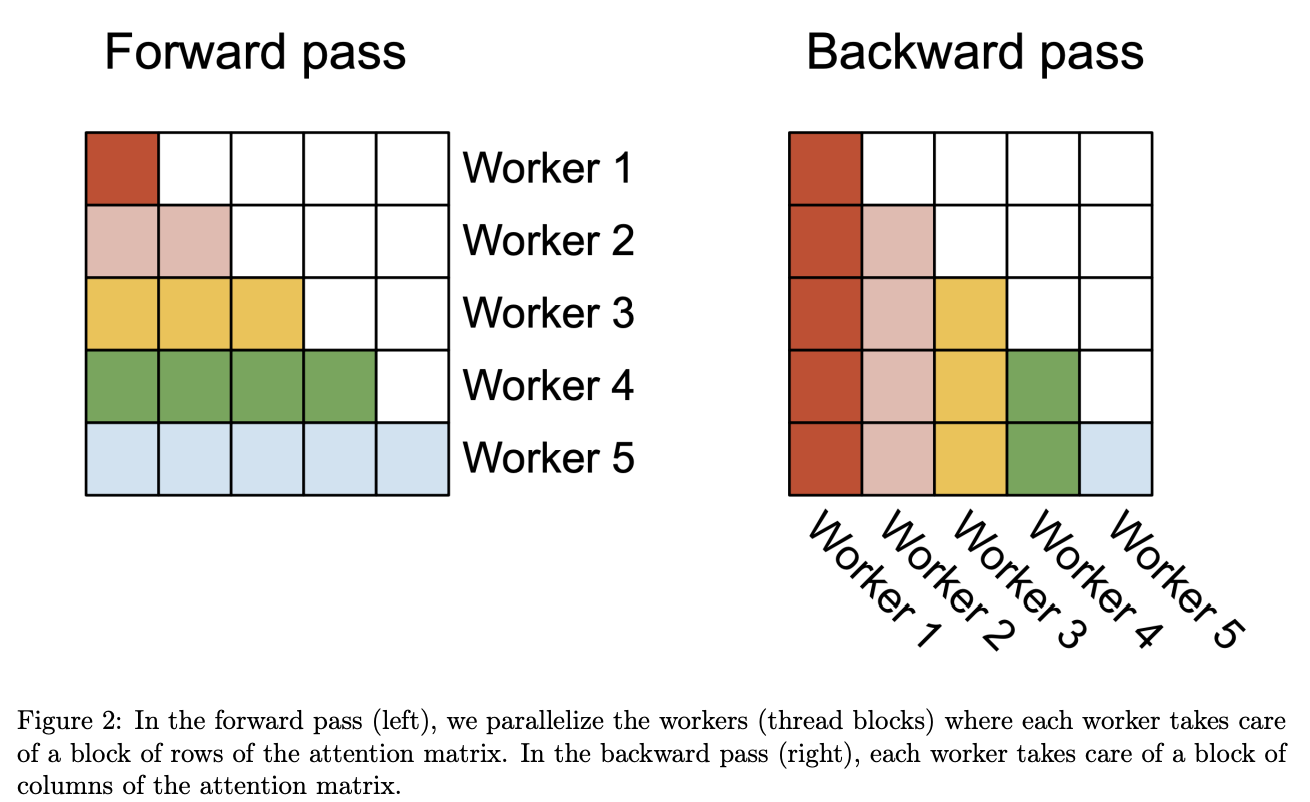
FWD：每一行（一个 $Q_i$）对应一个 thread block（$Q$ 为外循环，$K, V$ 为内循环）；
BWD：每一列（一个 $K_j, V_j$）对应一个 thread block（$K, V$ 为外循环，$Q$ 为内循环）。

Word Partitioning

针对 thread block 中 wraps 的组织优化。

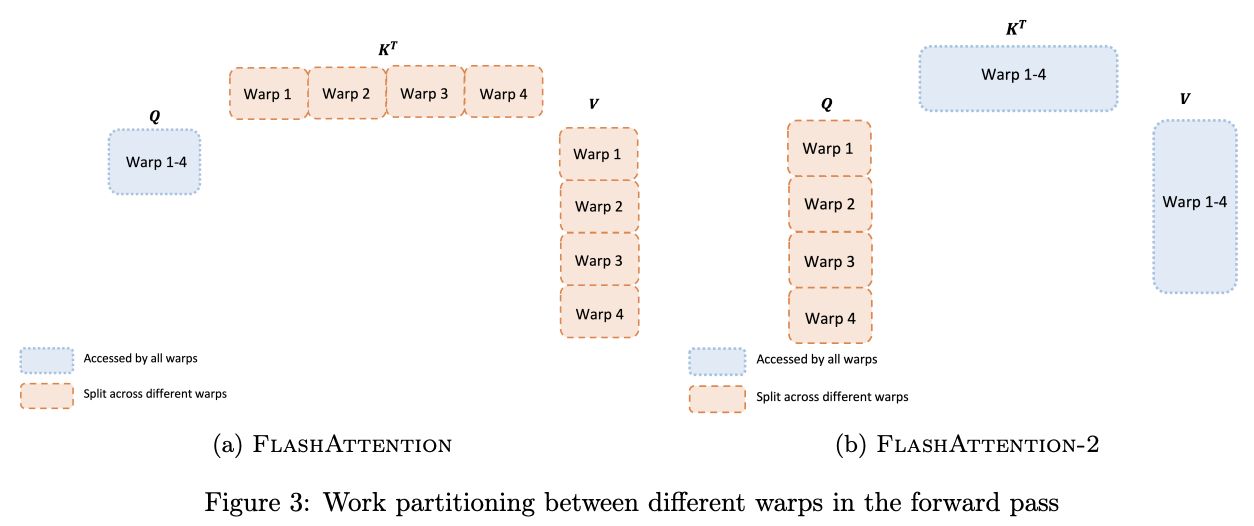
V1 对 $K, V$ 按照 seq_len 分成 wrap（对 $Q$ 不分块）：假设将 $K, V$ 切成4块得到 $K_1, K_2, K_3, K_4$ 和 $V_1, V_2, V_3, V_4$，大小均为 $(\frac{N}{4}, d)$. 每个 wrap 的 Self-Attention 计算流程如下：

\[ \begin{align*} S_i=QK_i^T\in\mathbb{R}^{N\times\frac{N}{4}} \\ P_i=softmax(S_i)\in\mathbb{R}^{N\times\frac{N}{4}} \\ O_i=P_iV_i\in\mathbb{R}^{N\times d} \\ \end{align*} \]

每一个 wrap 计算的输出 $O_i$ 写入共享存储区域；最终将结果叠加得到完整输出 $O$.

V2 对 $Q$ 按照 seq_len 分成 wrap（对 $K, V$ 不分块）：假设将 $Q$ 切成4块得到 $Q_1, Q_2, Q_3, Q_4$，大小均为 $(\frac{N}{4}, d)$. 每个 wrap 的 Self-Attention 计算流程如下：

\[ \begin{align*} S_i=Q_iK^T\in\mathbb{R}^{\frac{N}{4}\times N} \\ P_i=softmax(S_i)\in\mathbb{R}^{\frac{N}{4}\times N} \\ O_i=P_iV_i\in\mathbb{R}^{\frac{N}{4}\times d} \\ \end{align*} \]

V2 只需将每个 wrap 的结果直接拼接，warps 之间无需通信；另外减少了额外的加法及它对应的读写操作，因此 V2 的 wrap 拆分策略更高效。对比图如下：