并行训练系列：6. 序列并行上篇（Megatron-SP, DeepSpeed-Ulysses）

中间激活值的显存占用量

参考：https://lywencoding.com/posts/76aa9d6e.html

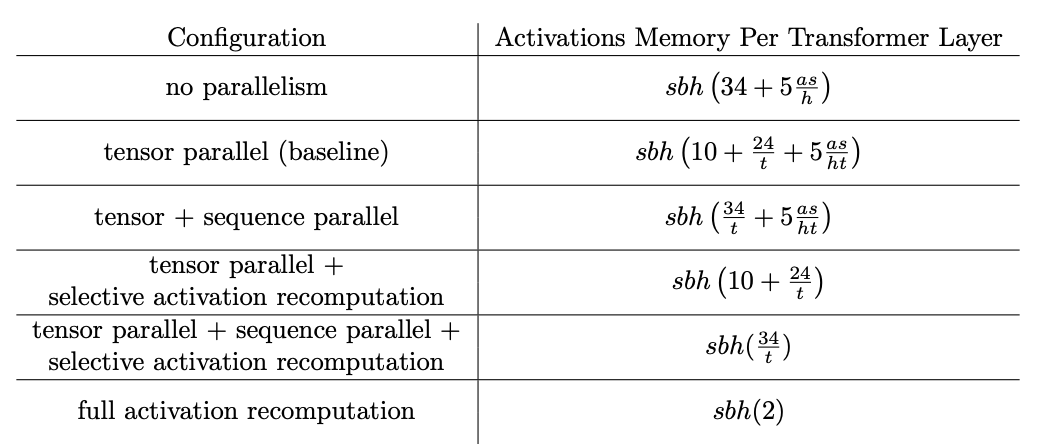
对 Transformer 在训练过程中的模型参数、中间激活值的显存占用量进行了分析。直接给出结论：

对于\(l\)层的 Transformer 模型：模型参数量为 \((12h^2+13h)*l\)；中间激活值为\((34bsh+5bs^2a)*l\)。

可以发现：模型参数的显存占用量与输入数据大小无关；中间激活值的显存占用量与输入数据大小（批次大小\(b\)和序列长度\(s\)）成正相关。

显存占用量随着批量大小线性增长，并随着序列长度的平方增长，那么：激活内存是最容易“膨胀”的部分；对于短序列（或者小批量大小），激活几乎可以忽略不计；但从大约 2-4k 个 token 开始，它们开始占用大量显存。

如何优化激活值的占用呢？有以下几种策略：

激活值重计算：抛弃 FWD 的部分激活值；在 BWD 时实时重新计算。（当前大多数框架使用 Flash Attention）
梯度累积：将 batch 拆分为若干个小的 micro-batch；依次在每个 micro-batch 上执行 FWD 和 BWD（多个 micro-batch 之间可以并行执行）并计算梯度，在执行优化步骤前，将所有 micro-batch 的梯度相加。
切分 TP 未处理的激活值：SP.

TP(+SP)

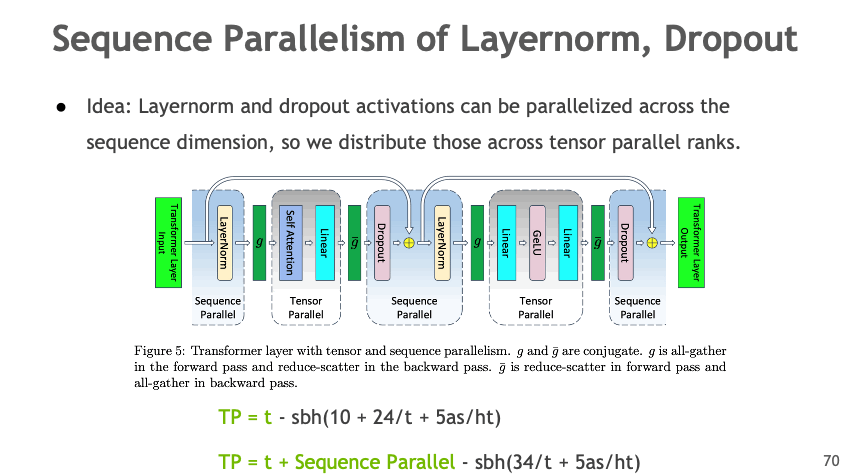
相较于 TP，TP+SP 保持了原始 TP Group 不变，只针对 Attn 和 MLP 的输入/输出部分做了 SP；SP 实际优化的部分是 LayerNorm 和 Dropout.

LayerNorm 和 Dropout 在 input sequence 维度上独立（LayerNorm 对每个 token 的 embedding 独立归一化；Dropout 对每个元素独立使用）。但是需要完整的隐藏层维度，例如：

\[ LayerNorm(x)=\gamma·\frac{x-\mu}{\sqrt{\sigma^2+\epsilon}}+\beta \]

其中，\(\mu=mean(x), \sigma^2=var(x)\)是沿着隐藏层维度\(h\)计算的。

假设 TP Group 的大小为 tp_size ，输入为\((s,b,h)\)，SP 的做法是将\(s\)分成 tp_size 份，即每个 TP Group 只处理 seq 的一部分；

由于 Attn 是序列依赖的（Query 需要和序列中所有的 Key 交互），因此计算 Attn 前需要将各个 GPU 上的序列 all-gather，恢复完整序列。

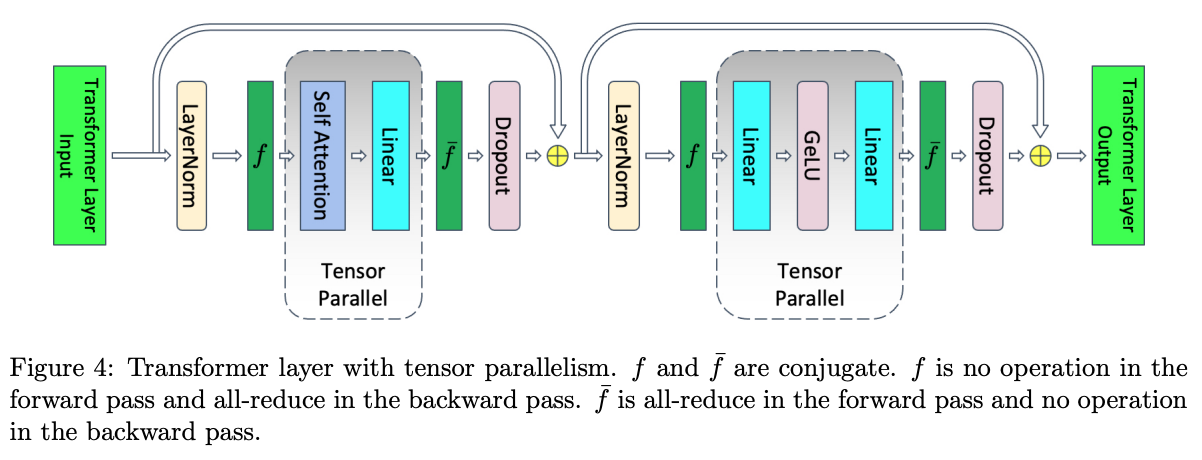
TP：

前向传播：
- \(f\)是一个 no-op，因为激活值已经在不同的 rank 之间完成复制；
- \(\overline{f}\)是一个 all-reduce，用于同步激活值。
反向传播：
- \(\overline{f}\)是一个 no-op，因为梯度已经在不同的 rank 之间完成复制；
- \(f\)是一个 all-reduce，用于同步梯度。

TP+SP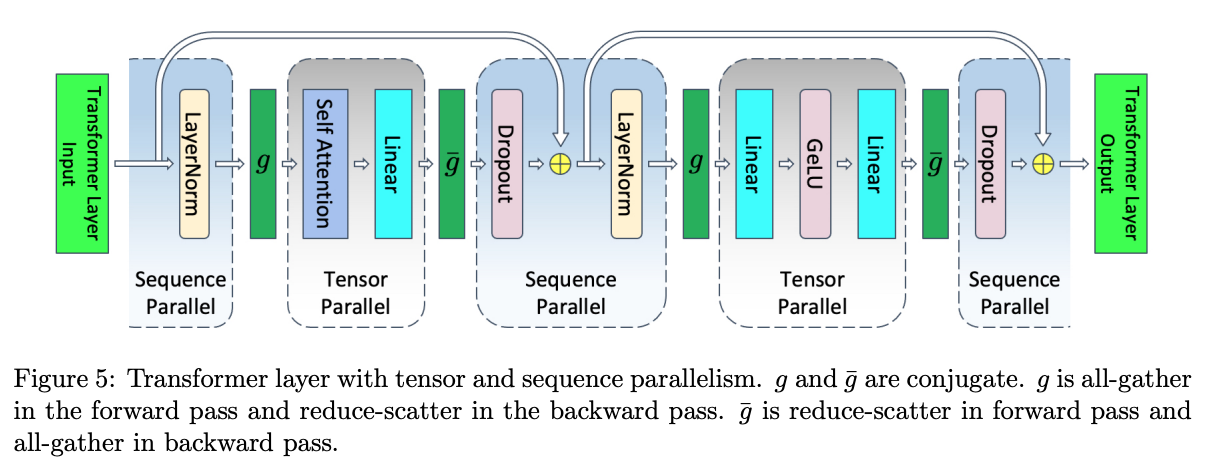： MLP 层前后详细的处理流程如下：

前向传播：

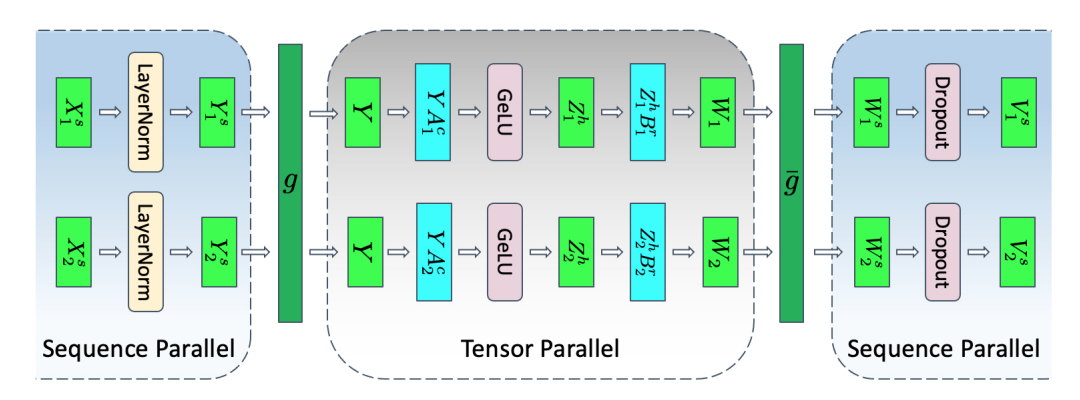
初始层归一化（SP 区域）
- 输入张量 X1 和 X2（形状为 b, s/2, h）进入 LayerNorm，已经沿 sequence 维度进行拆分，每个 GPU 独立计算各自序列块的LayerNorm，得到 Y1 和 Y2；
第一次转换（SP -> TP）：\(g\) 是一个 all-gather，Y1 和 Y2 合并回完整的序列长度并恢复 Y（形状为 b, s, h）
第一次线性变换（TP区域）：A1 层是 column-linear，沿隐藏维度拆分 Y；GeLU 激活函数在每个 GPU 上独立应用 Z1，形状为 (b, s, h/2)
第二次线性变换（TP区域）：B1层是 row-linear，它恢复隐藏维度 W1 形状为 (b, s, h)
最后转换（TP -> SP）：\(\overline{g}\)是一个 reduce-scatter，在前一个 row-linear 层的进行 dropout，同时在 sequence 维度上进行分散；W1形状为 (b, s/2, h)

反向传播：

\(\overline{g}\) 是一个 all-gather，让每张卡拿到完整的\(\frac{\partial L}{\partial Z}\)的结果；
- BWD 中 TP 来到 Y 时，由于 Y 来自 FWD 中\(g\)对 LayerNorm 的输出结果做 all-gather 得到，在 BWD 中为了拿到 Y 以便于梯度顺利传导，再做一次 all-gather（可以在梯度传导到 Y 之前就 all-gather，以便将该通信时间与计算重叠，故不计入）
\(g\)是一个 reduce-scatter，让每张卡拿到自己维护的 seq 片段的\(\frac{\partial L}{\partial X}\).

TP(+SP) 单卡激活值大小分析

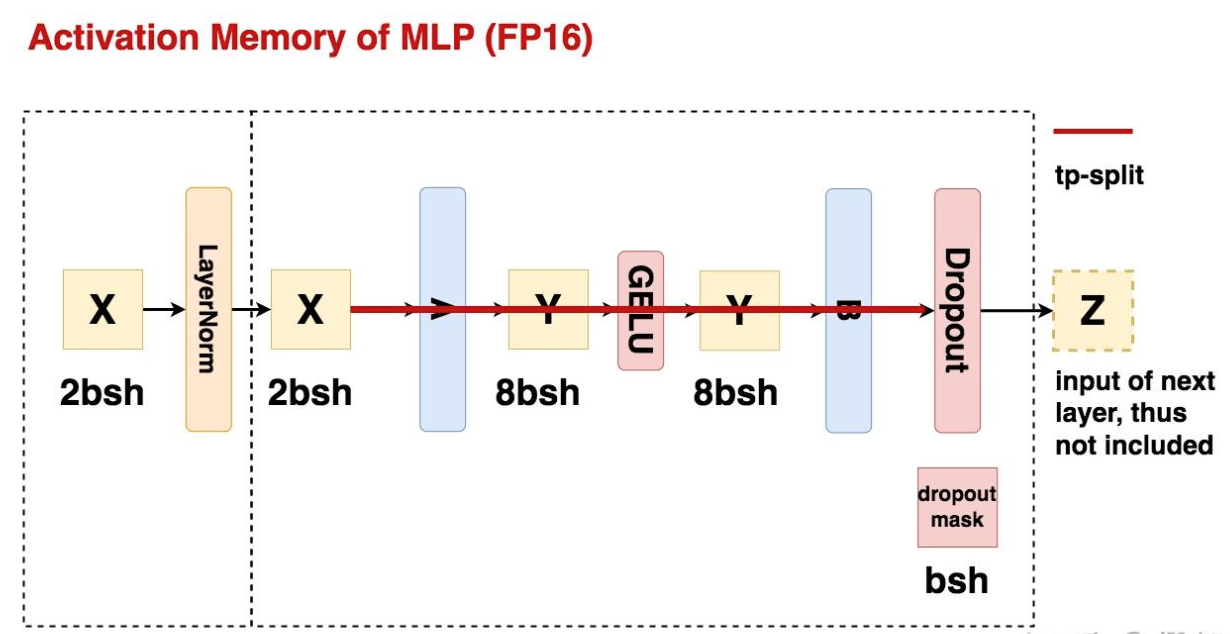
MLP 层

MLP 的总激活值大小为 \(19bsh\).（考虑 LayerNorm 的输入一共\(21bsh\)）

计算 TP 时单卡激活值大小：

LayerNrom 前后每张卡重复保存输入输出：\(4bsh\)；
MLP 的 TP Group 切分激活值，单卡保存：\(\frac{16bsh}{t}\)；
TP 先做 all-reduce 聚合输出再做 dropout（因此 dropout mask 也重复保存），单卡保存：\(bsh\).

TP 单卡激活值大小为：\(5bsh+\frac{16bsh}{t}\)

计算 TP +SP 时的单卡激活值大小：

LayerNorm 的输入按照 seq 维度切分，因此输入输出的激活值大小由\(4bsh\)降低至\(\frac{4bsh}{t}\)；
正常执行 TP，该阶段单卡激活值为\(\frac{16bsh}{t}\)；
TP -> SP 时\(\overline{g}\)做一次 reduce-scatter（每张卡只需要拿到自己的 seq 片段对应输出，因此不需要 all-reduce）；
每张卡独立做 dropout，单卡上的 dropout mask 激活值由\(bsh\)降为\(\frac{bsh}{t}\)；

相比纯 TP，TP+SP 的单卡激活值大小将其\(5bsh\)继续切分为\(\frac{5bsh}{t}\)，单卡总激活值大小为\(\frac{21bsh}{t}\).

Attn 层

TP 时单卡激活值大小为\(5bsh+\frac{5bs^2a+8bsh}{t}\)；TP+SP 时单卡激活值大小为\(\frac{5bsh}{t}+\frac{5bs^2a+8bsh}{t}\)。SP 额外切分的也是 LayerNorm 的输入输出和最后一个 dropout mask 矩阵。

选择性重计算

有时即使采用了 TP+SP，激活值也可能存不下，是不是可以选择性保存呢？由于 Attn 层显存占用量大、计算量本身不大的激活值（Attn 激活值随着序列呈平方增长；用于 attention score 的 softmax 比矩阵乘法更快），因此抛弃它们。

DeepSpeed Ulysses

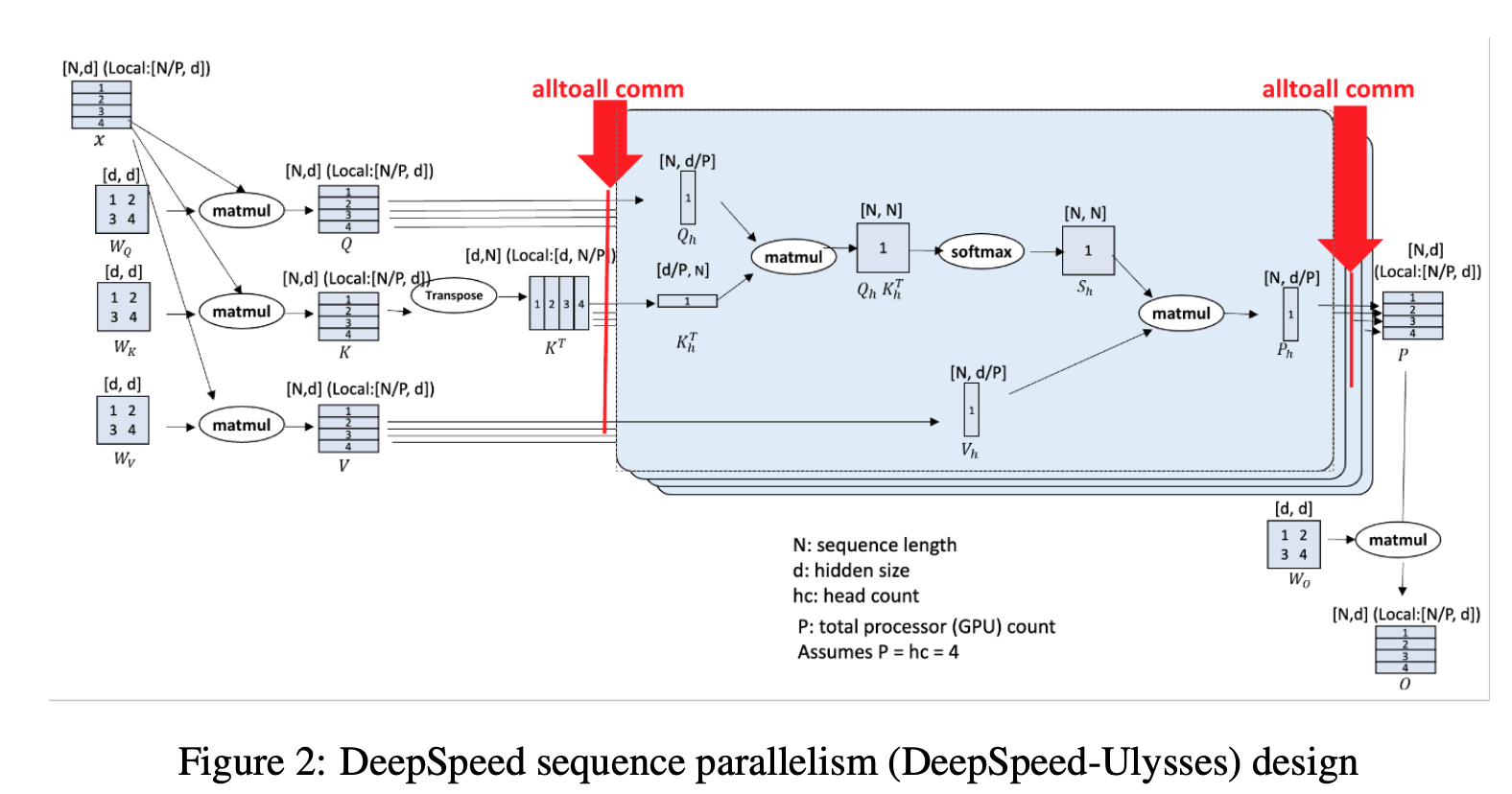
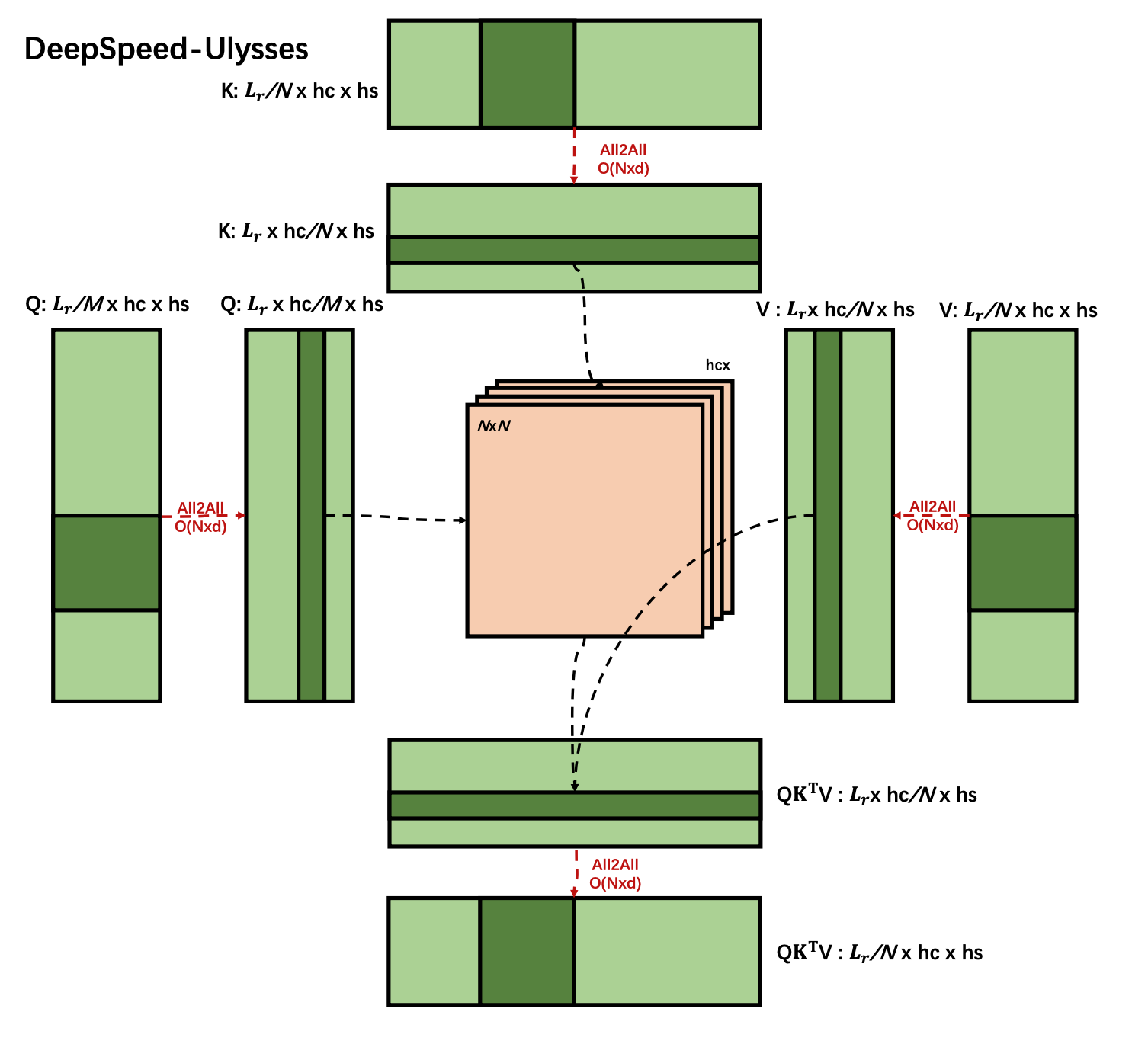
对比以下两张图（来自 paper），观察核心设计：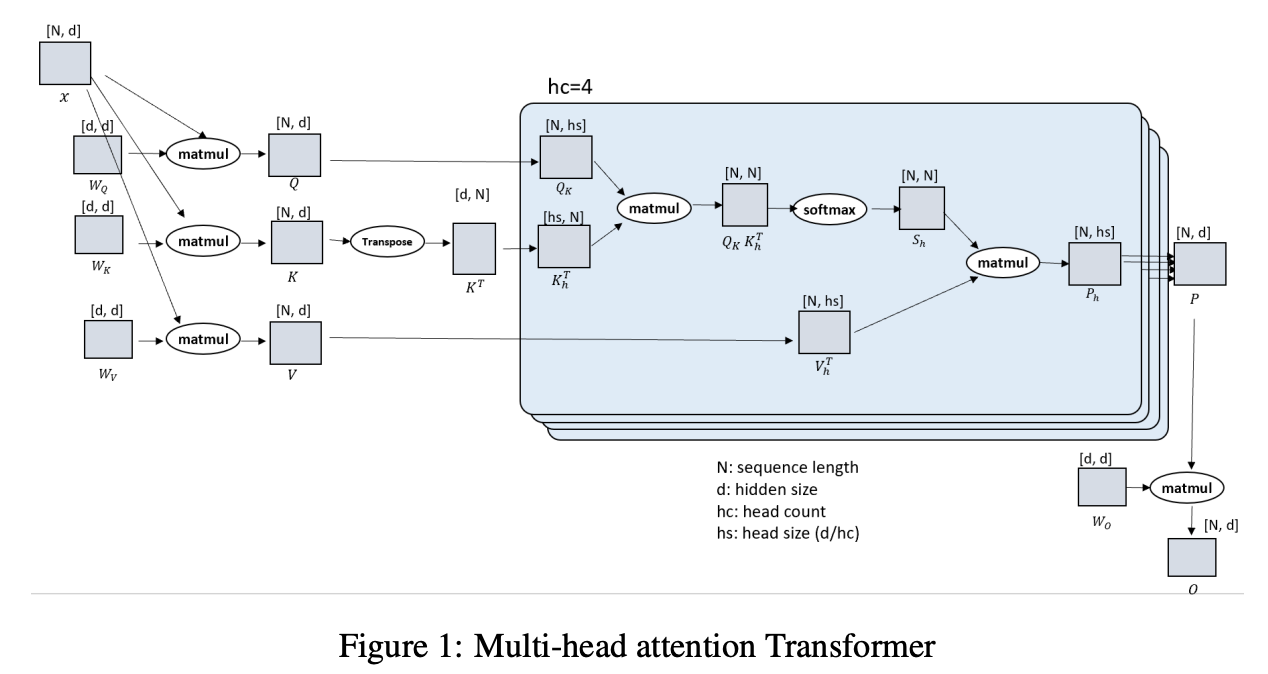

DS-Ulysses 的核心理念是：对 Q, K, V 沿着 seq 维度（N）切分，

前向传播：

按 seq 维度切分输入 X，每张卡上 seq_chunk 尺寸为(N/P, d)；分别与完整的\(W_Q\), \(W_K\), \(W_V\) 矩阵相乘，得到 Q, K, V；
- 注意：每张卡上保存完整模型（尺寸为(d, d)的\(W_Q\), \(W_K\), \(W_V\)）。与 ZeRO-3 配合使用时，计算前每张卡上保存部分模型，但是要通过 all-gather 拿回完整模型再开始计算，实质上是 DP.
针对按 seq 维度切分的 q_chunk/k_chunk/v_chunk，所有卡之间做一次 All2All 通信，使得每张卡分别拿到所有 seq 的某一个 head 的 q_chunk/k_chunk/v_chunk.（All2All 实际上是矩阵转置操作）
每张卡分别计算 Attention，输出尺寸为(N, d/P)；
所有卡之间再做一次 All2All 通信，单卡上维护的输出尺寸回到(N/P, d)；再与单卡上完整的\(W_O\)矩阵相乘，得到单卡最后的输出，对应一个 seq_chunk 的 loss，尺寸为(N/P, d).
进入 MLP 层，由于不涉及 token 之间的相关性计算，因此每个 seq_chunk 可以单独计算。

Megatron-SP 与 Ulysses 通信量分析

Megatron VS Ulysses：

Megatron-SP 通过 TP 显式地将\(W_q\), \(W_k\), \(W_v\) 切分到不同的 TP Group，每张卡上计算所有 seq 的某个 head 的结果；
Ulysses 通过 SP + All2All，在每张卡上完整保存 \(W_q\), \(W_k\), \(W_v\) 的前提下，让每张卡上计算所有 seq 的某个 head 的结果。

Megatron

Attn 层：

FWD 做了一次 all-gather 和一次 reduce-scatter；
BWD 做了一次 reduce-scatter 和一次 all-gather.

MLP 层：也是2次 all-gather 和2次 reduce-scatter.

忽略 batch_size，一次 all-gather/reduce-scatter 的通信量为 Nd，则 MLP 层+Attn 层的总通信量为8Nd.

DeepSpeed Ulysses

一次 All2All 操作的通信量：

All2All 操作之前，每张卡上的 seq_chunk 的数据大小为 (Nd)/P，seq_chunk 中的小数据块大小为 (Nd)/(PP).

**单卡发送的通信量为 [(Nd)/(PP)]*(P-1)，近似为 (Nd)/P**.

FWD：

q_chunk/k_chunk/v_chunk 各执行一次 All2All 操作，单卡总通信量为 3ND/P；
做一次 All2All 聚合每张卡上的 Attn 计算结果，单卡总通信量为 Nd/P.

BWD：在 FWD 的相同位置做 All2All 操作，共4次，单卡总通信量为 4Nd/P.

BWD 中和计算时间重叠的通信量：
激活值重计算；
梯度的 AllReduce.
举个例子，BWD 中计算\(W_O\)的梯度，每张卡上维护一个 seq_chunk 的 P_chunk 结果：有：\(O_k=P_k\times W_o\)，完整序列的 loss 为 \(L=\sum_{i=1}^P f(O_i)\)，因此：\(\frac{\partial L}{\partial W_O}=\sum_{i=1}^P \frac{\partial L_i}{\partial W_O}\)，需要通过 AllReduce 得到所有卡的梯度再求和。
由于梯度的 AllReduce 与链式传导相对独立，因此 AllReduce 操作可以与 BWD 计算重叠。

综上，FWD+BWD 中 Ulysses 的单卡总通信量为 8Nd/P.

Ulysses 的核心优势是单卡通信量低，可以通过同比增加 GPU 数量抵消通信量随序列长度线性增长的效应。

Megatron 的单卡通信量恒为 8Nd，如果序列长度增加（N 变大），无法通过扩张卡的数量解决；
Ulysses 的单卡通信量为 8Nd/P，当序列长度增加时，可以通过同倍数增加 GPU 数量（P），使得单卡通信量维持一个常数。

然而，Ulysses 的 GPU 数量 P 也无法无限扩张。因为 All2All 操作后切分维度 d/P，希望 d/P=hc/P * head_size，即切分 head_cnt 维度，使得 Attn 计算能在单卡上完成（便于使用 FlashAttention 等单卡优化技术）。但是，如果使用 GQA 或者 MQA，K, V 的 head_cnt 较小，限制了 P 的增加（P 不能超过 head_cnt）.

Ulysses + ZeRO-3：模型权重在 DP ranks 和 SP ranks 两个维度上切分，需要获取时通过 all-gather 聚合。

另一个经典的 SP 工作 Ring-Attention 见下篇。