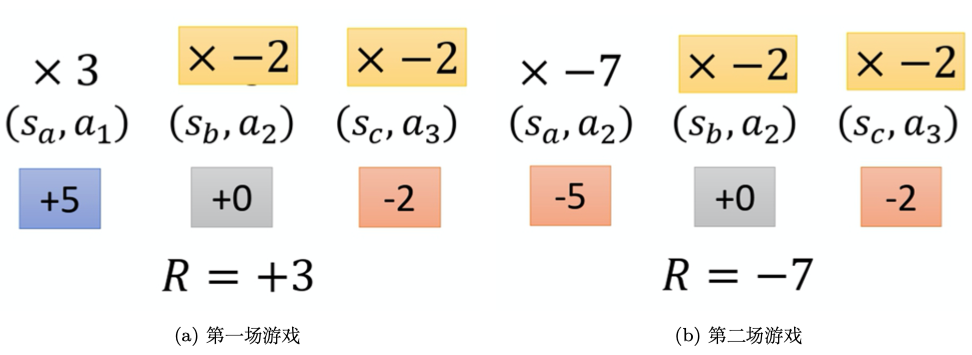RL 系列:4. 策略梯度算法
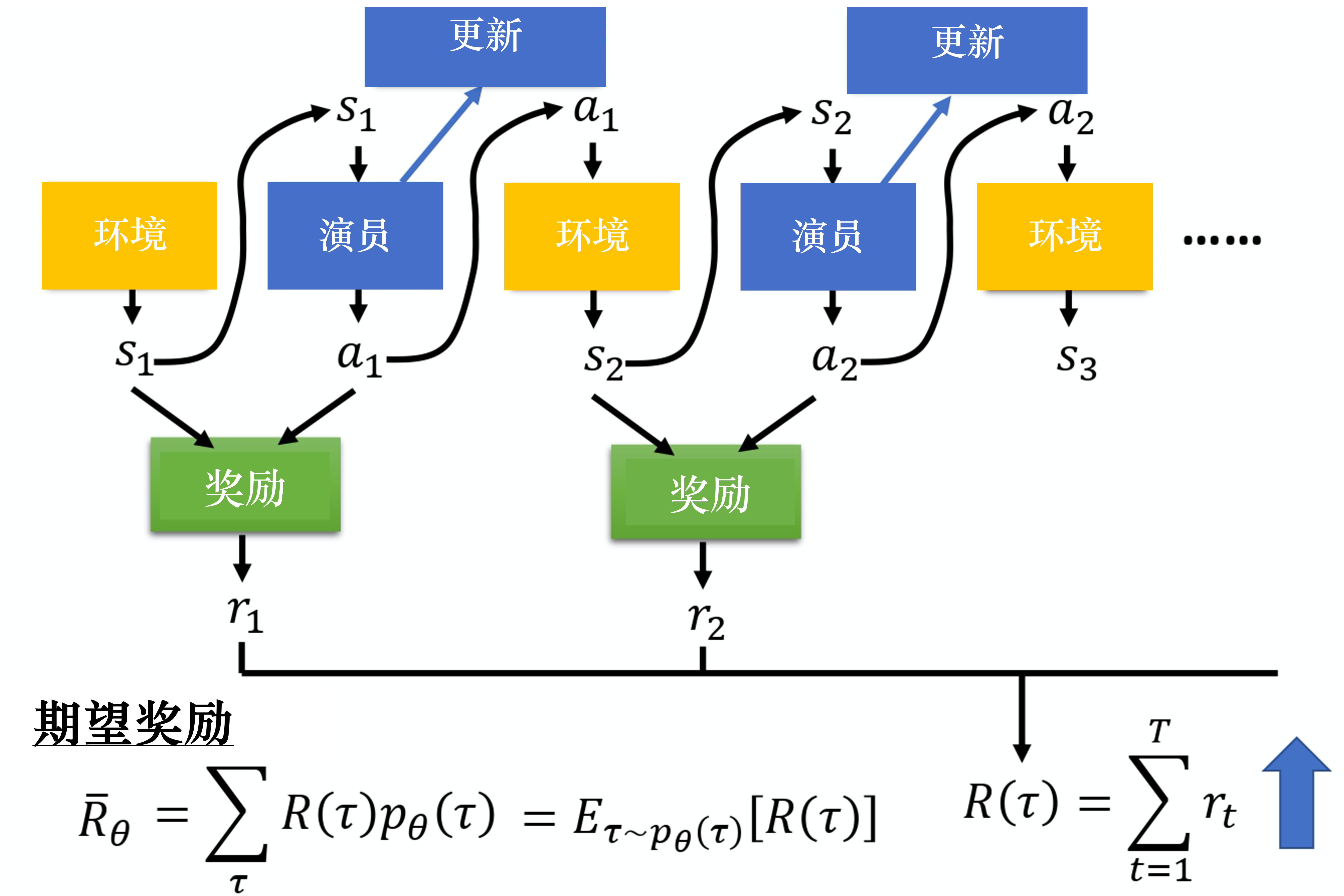
RL 的三个组成部分为:Actor, Environment 和 Reward. Environment 和 Reward 在 RL 学习开始前已经决定,要求是寻找 Actor 的最优策略以最大化 Reward.
假设轨迹为:
\[ \tau=\{s_1, a_1, s_2, a_2, ..., s_t, a_t\} \]
给定 Actor 的参数\(\theta\)(策略\(\pi\)中的网络参数\(\theta\)),某个轨迹\(\tau\)发生的概率为:
\[ p_{\theta}(\tau)=p(s_1)\prod_{t=1}^Tp_{\theta}(a_t|s_t)p(s_{t+1}|s_t,a_t) \]
其中\(p(s_{t+1}|s_t,a_t)\)由环境决定;\(p_{\theta}(a_t|s_t)\)由策略\(\pi\)决定,也即 RL 的优化目标。
期望奖励为:
使用梯度上升最大化期望奖励:
\[ \nabla\overline{R_{\theta}}=\sum_\tau R(\tau)\nabla p_\theta(\tau) \]
有:
\[ \begin{align*} \nabla\overline{R_{\theta}}&=\sum_\tau R(\tau)p_\theta(\tau)\frac{\nabla p_\theta(\tau)}{p_\theta(\tau)} \\ &=\sum_\tau R(\tau)p_\theta(\tau)\nabla\log p_\theta(\tau) \\ &=\mathbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log p_\theta(\tau)] \end{align*} \]
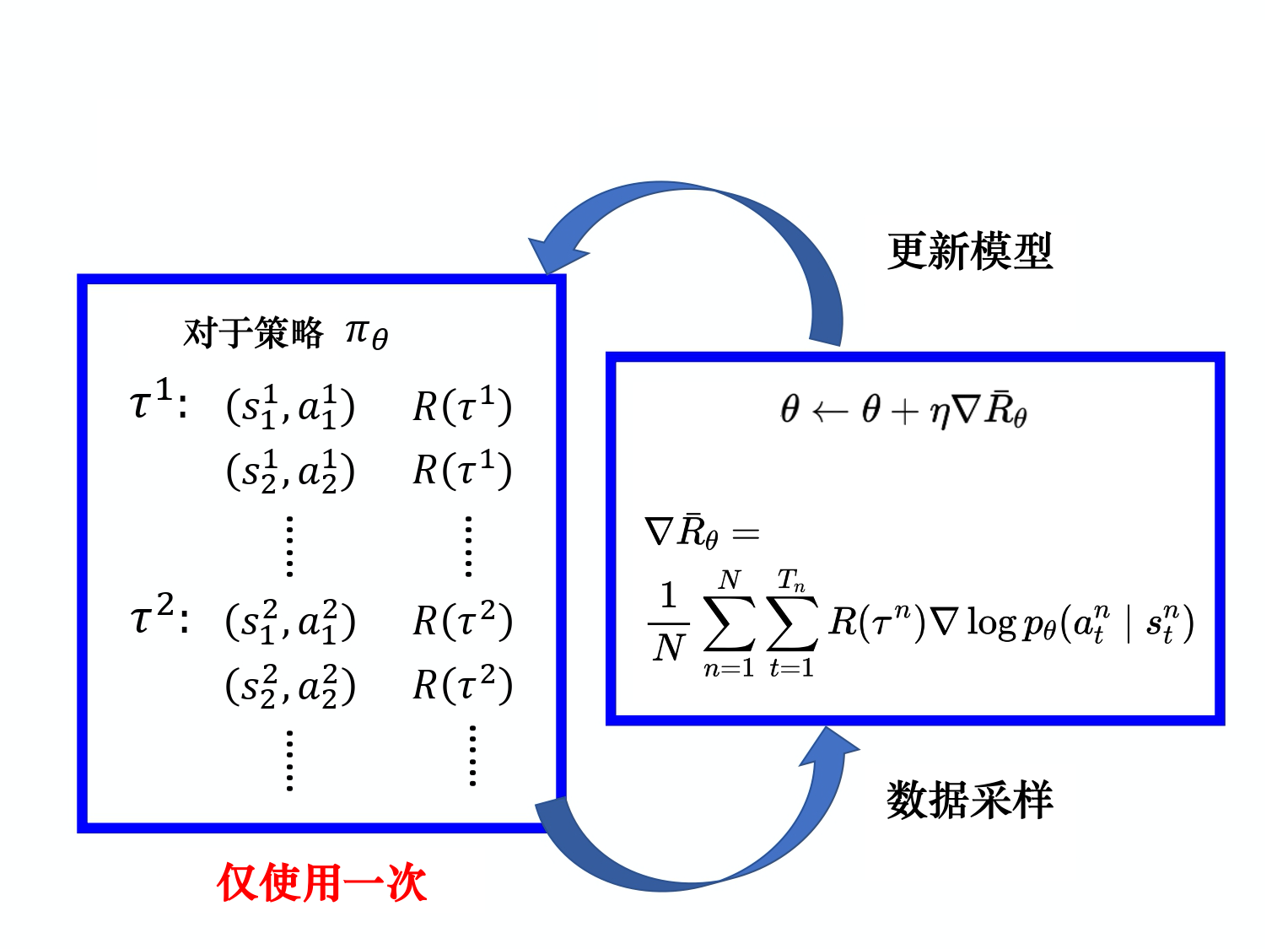
采样\(n\)个轨迹\(\tau\),近似估计:
\[ \begin{align*} \mathbb{E}_{\tau\sim p_\theta(\tau)}[R(\tau)\nabla\log p_\theta(\tau)]&\approx \frac{1}{N}\sum_{n=1}^N R(\tau^n)\nabla\log p_\theta(\tau^n) \\ &=\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n)\nabla\log p_\theta(a_t^n|s_t^n) \end{align*} \]
策略更新方式为:
\[ \theta\leftarrow\theta+\eta\nabla\overline{R_\theta} \]
策略梯度算法为on-policy算法,因为必须使用当前策略\(\pi_\theta\)采样得到的数据计算梯度(期望\(\mathbb{E}\)的下标包含\(\theta\));一般策略梯度采样的数据只使用一次。采样数据->更新参数->重新采样数据。
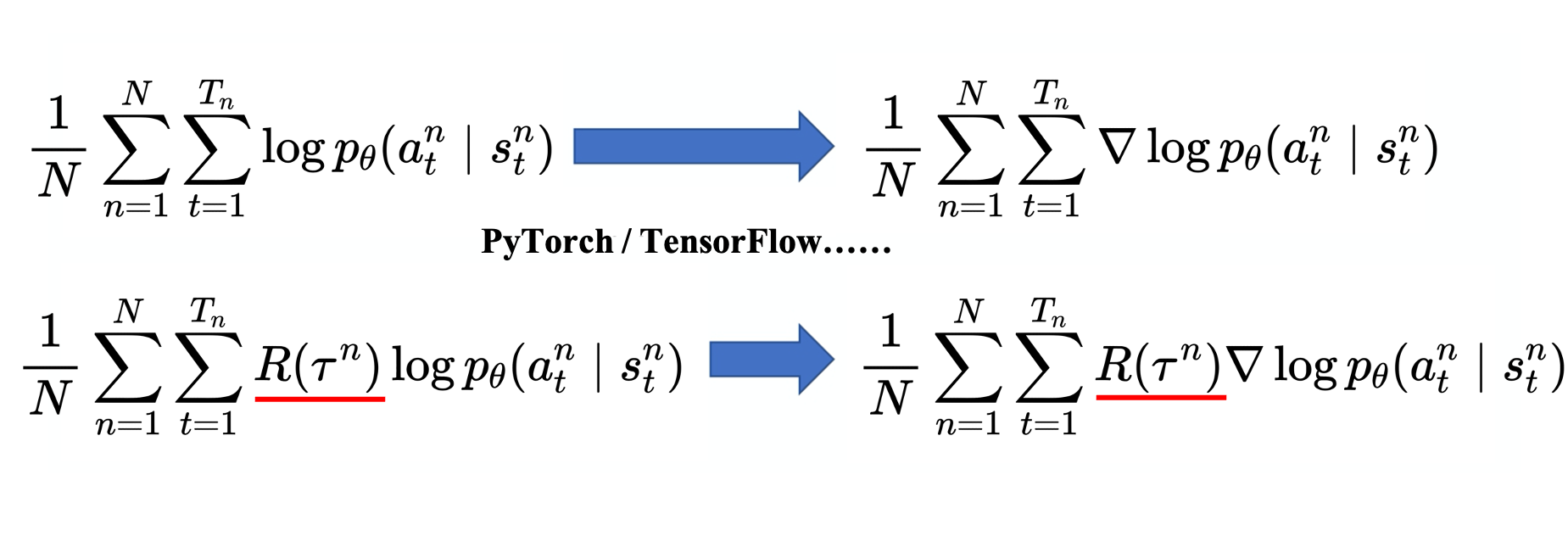
对于分类问题,目标函数为:
\[ \frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n}\nabla\log p_\theta(a_t^n|s_t^n) \]
强化学习与分类问题唯一不同的地方在于:loss 之前乘一个权重,即整场游戏得到的总奖励\(R(\tau)\).
一些优化
添加 baseline
当前\(\nabla\overline{R_\theta}\)恒为正,那么没有被采样的动作的概率将会下降(然而未被采样的动作不一定不好)。因此希望奖励不总是正的。
奖励减\(b\),重新定义为:
\[ \nabla\overline{R_\theta}=\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} (R(\tau^n)-b)\nabla\log p_\theta(a_t^n|s_t^n) \]
其中\(b\)为基线,令\(b\approx E[R(\tau)]\).在训练过程中,不断地记录和更新\(b\),此时\(R(\tau)\)有正有负。
每个动作分配合适分数
同一条轨迹中的所有状态-动作对均采用相同的权重\(R(\tau)\)(总奖励)是不合适的。
一种改进方式:计算某个状态-动作对的权重时,原先的权重是整场游戏的奖励总\(R(\tau)\),现在改为从该动作对应的时刻\(t\)开始,到游戏结束的奖励总和;同时加上未来的折扣因子。
即:
\[ \nabla\overline{R_\theta}=\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} (\sum_{t'=t} ^{T_n}\gamma^{t'-t}r_{t'}^n-b)\nabla\log p_\theta(a_t^n|s_t^n) \]
将\(R-b\)这一项称为优势函数,由\(A^\theta(s_t, a_t)\)表示(\(b\)由状态决定,使用一个网络进行估计);优势函数的意义为:在状态\(s_t\)处执行动作\(a_t\),相较于执行其他动作的优势。
策略梯度算法
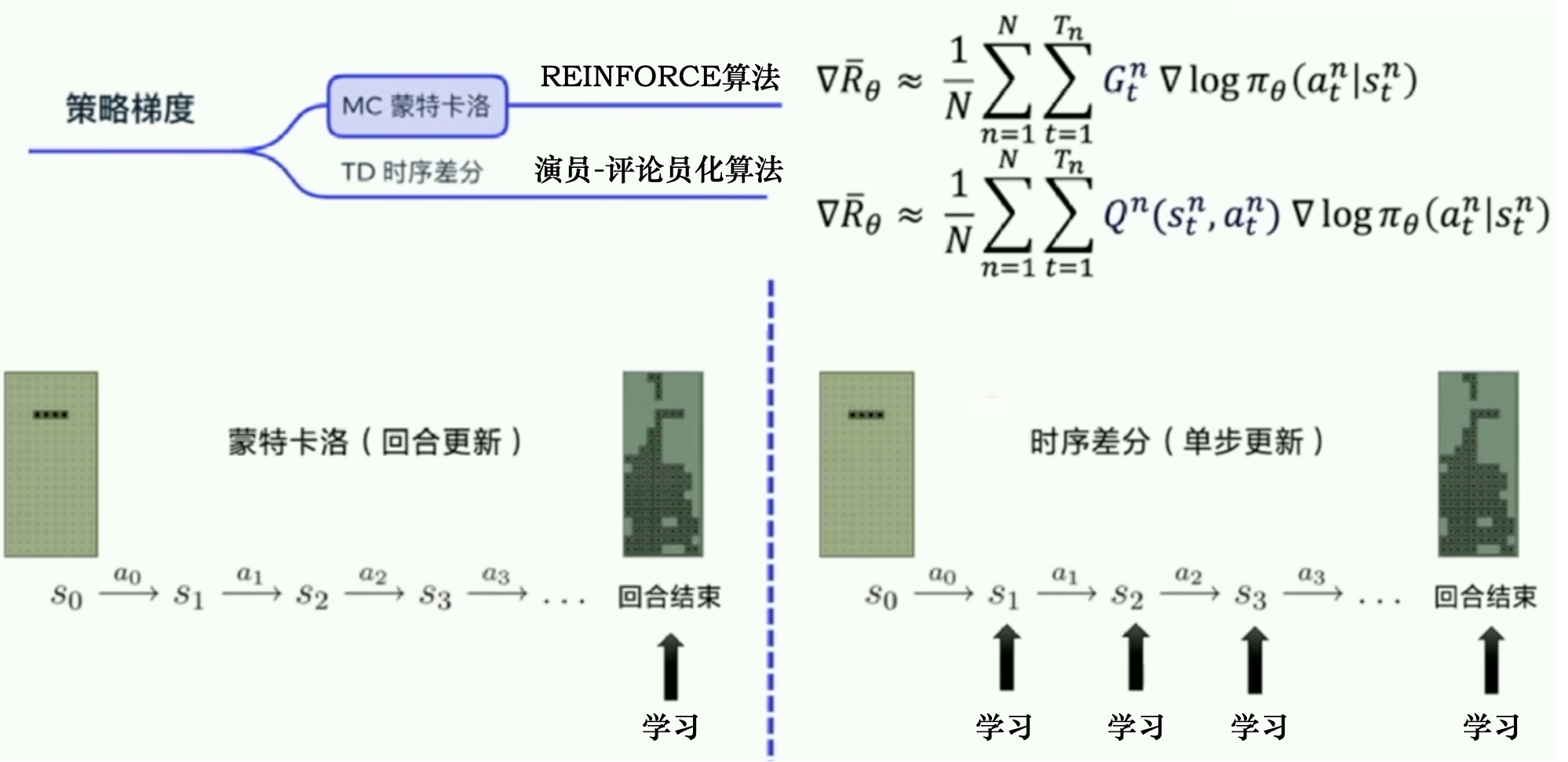
REINFORCE:蒙特卡洛策略梯度
蒙特卡洛一个回合更新一次;时序差分每个步骤更新一次。
REINFORCE 采取回合更新,先产生一个回合的数据:
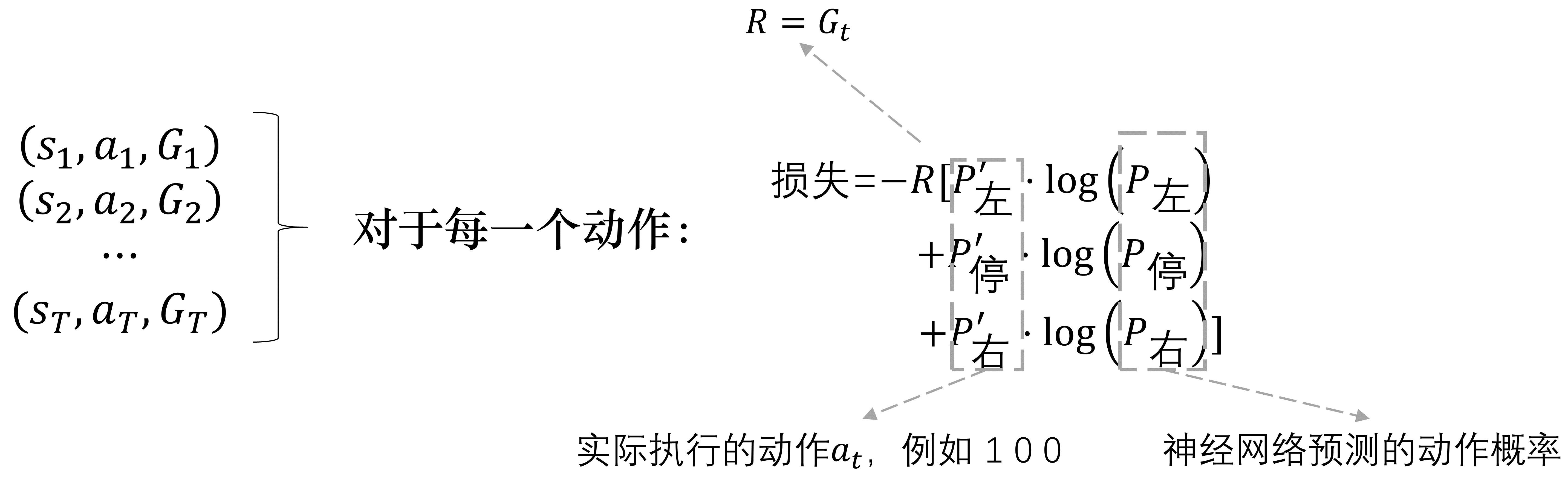
\[ (s_1, a_1, G_1), (s_2, a_2, G_2), ..., (s_T, a_T, G_T) \]
其中\(G_t\)代表每个步骤的未来总奖励,由于\(G_t=r_{t+1}+\gamma G_{t+1}\),因此可以从后向前推,从\(G_T\)计算到\(G_1\).
再针对每个动作\(a_t\)计算梯度\(\nabla \log\pi(a_t|s_t, \theta)\):先对实际执行的动作取独热向量,再获取神经网络预测的动作概率,将它们相乘。
期望奖励写为:
\[ \nabla\overline{R_\theta}\approx\frac{1}{N}\sum_{n=1}^N \sum_{t=1}^{T_n} G_t^n\nabla\log p_\theta(a_t^n|s_t^n) \]
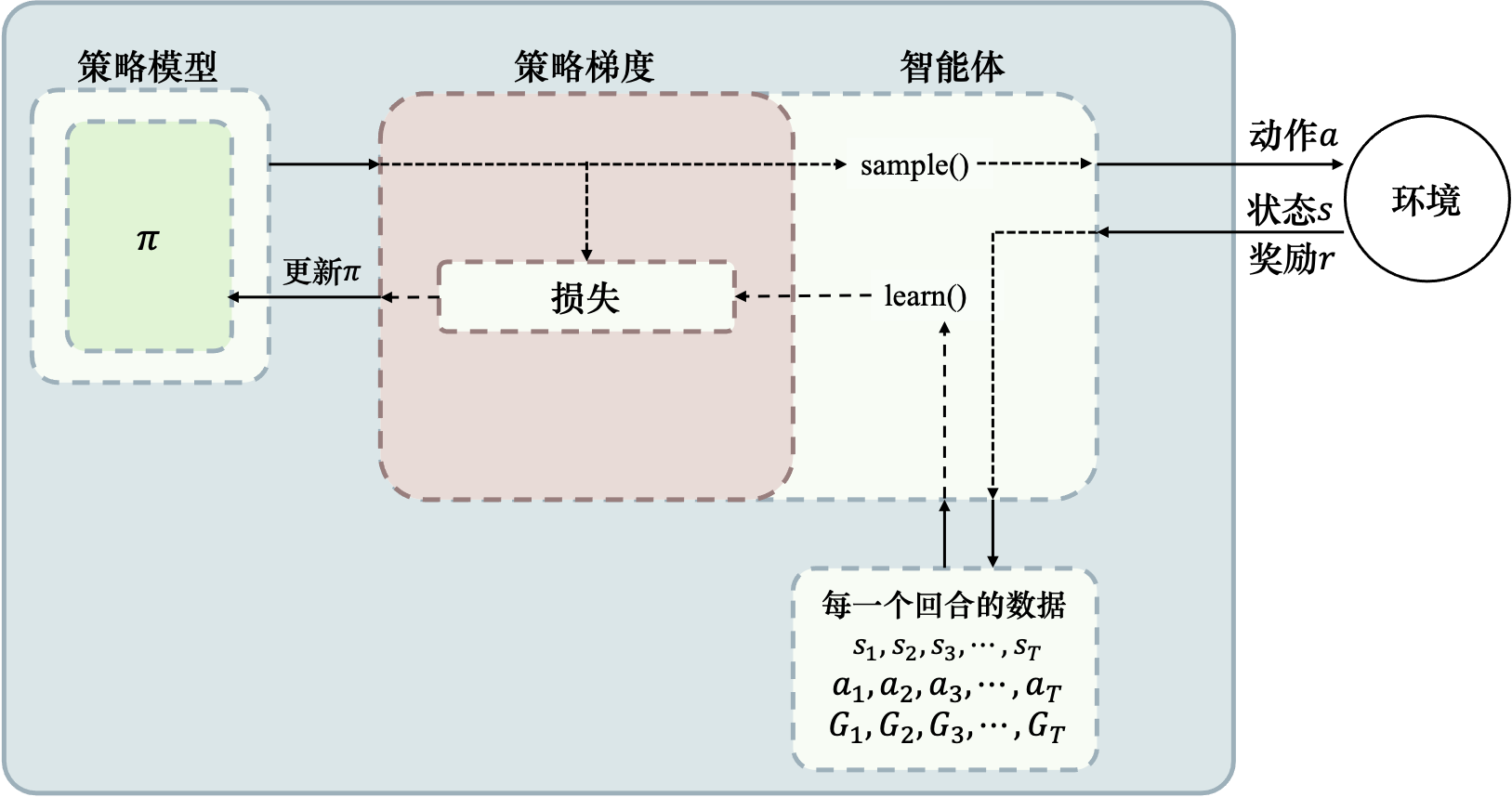
下图展示 REINFORCE 算法的流程:
- 策略模型输出动作概率;
- 通过 sample() 函数获取一个具体动作;
- 与环境交互得到整个回合的数据;
- 执行 learn() 函数,使用数据构造 loss 并更新策略模型(on-policy).
Actor-Critic 算法
REINFORCE 算法每次根据一个策略采集一条完整的轨迹,并计算这条轨迹上的回报。这种采样方式方差较大,学习效率较低。
Actor-Critic 算法结合策略梯度和时序差分,Actor 对应策略函数\(\pi_\theta(a|s)\),即学习一个策略以最大化 Reward;Critic 对应价值函数\(V_\pi(s)\),用于对当前策略的值函数进行估计,即评估 Actor 的好坏。
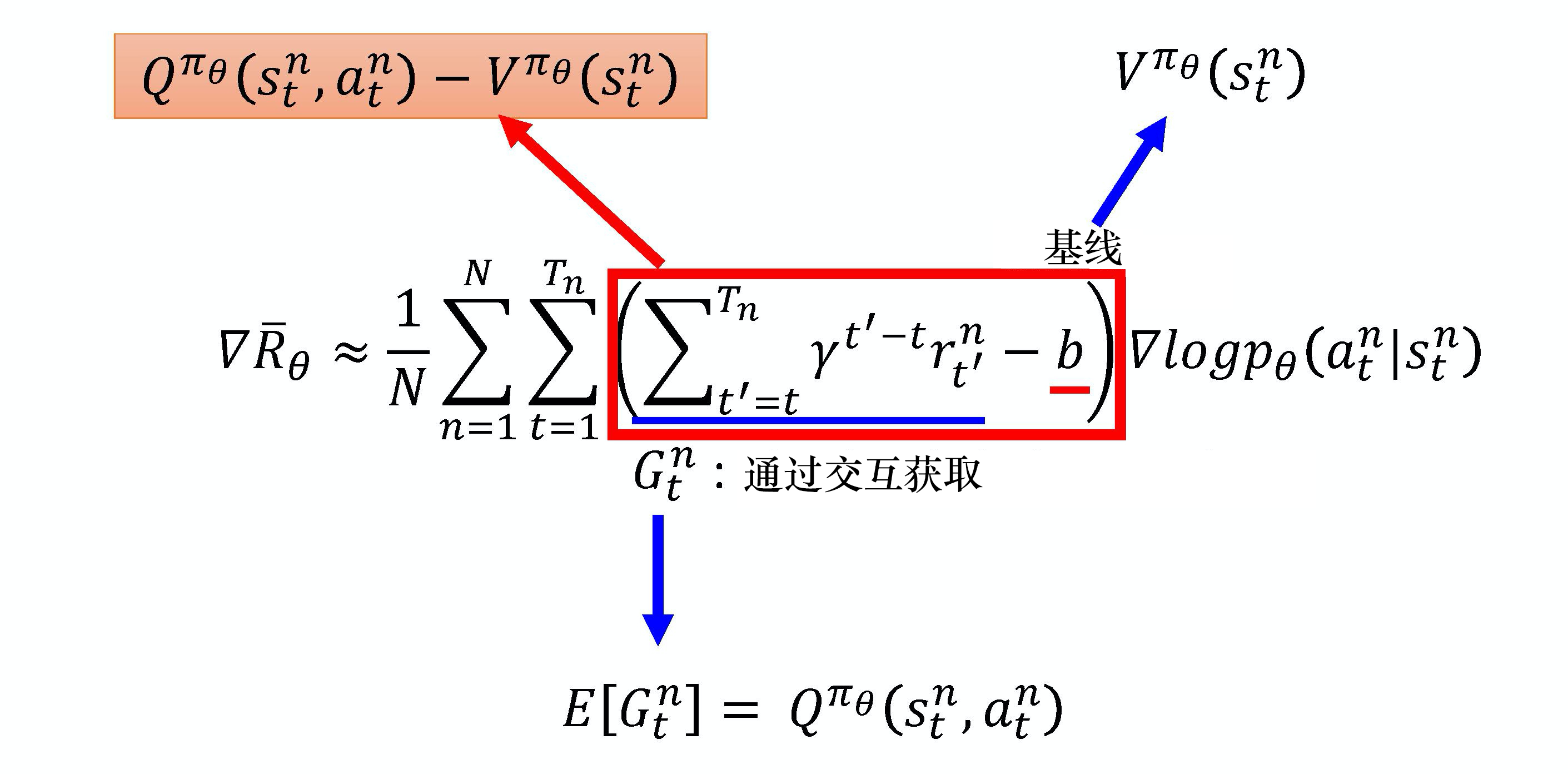
在策略梯度公式中,每个步骤的奖励\(G\)是一个随机变量,对于指定的状态\(s\)和动作\(a\)有一个固定分布。REINFORCE 的做法是采样直到游戏结束,统计所有奖励作为\(G\);现在希望直接估计随机变量\(G\)的期望值。
\(G\)的期望值为:\(\mathbb{E}[G_t^n]=Q_{\pi_\theta}(s_t^n, a_t^n)\);利用价值函数\(V_{\pi_\theta}(s_t^n)\)表示 baseline,含义为:在某个状态\(s\)一直与环境交互直至游戏结束的期望奖励。(\(V_{\pi_\theta}(s_t^n)\)不涉及动作,是\(Q_{\pi_\theta}(s_t^n, a_t^n)\)的期望值。
此时需要同时估计\(Q\)网络和\(V\)网络。由于:
\[ Q_{\pi_\theta}(s_t^n, a_t^n)=\mathbb{E}[r_t^n+V_{\pi}(s_{t+1}^n)] \]
此时只需要估计\(V\)网络了。策略梯度写为:
\[ \nabla\overline{R_\theta}\approx\frac{1}{N}\sum_{n=1}^N\sum_{t=1}^{T_n}(r_t^n+V_\pi(s_{t+1}^n)-V_\pi(s_{t}^n))\nabla\log p_\theta(a_t^n|s_t^n) \]