有模型 vs 免模型

有模型的强化学习：知晓状态转移函数（\(P[s_{t+1}, r_t|s_t, a_t]\)）和环境的奖励函数（\(R[s_t, a_t]\)），可通过策略迭代或价值迭代寻找最佳策略；智能体与环境无交互。

免模型的强化学习：状态转移函数和概率函数未知，非马尔可夫决策过程，无法直接采用动态规划。智能体和环境交互，通过采样到的数据学习。

免模型预测方法

蒙特卡洛策略评估

蒙特卡洛方法是一种基于概率统计的数值计算方法。一个例子是计算圆的面积：在正方形内部随机产生若干个点，细数落在圆中点的个数，圆的面积与正方形面积之比就等于圆中点的个数与正方形中点的个数之比。

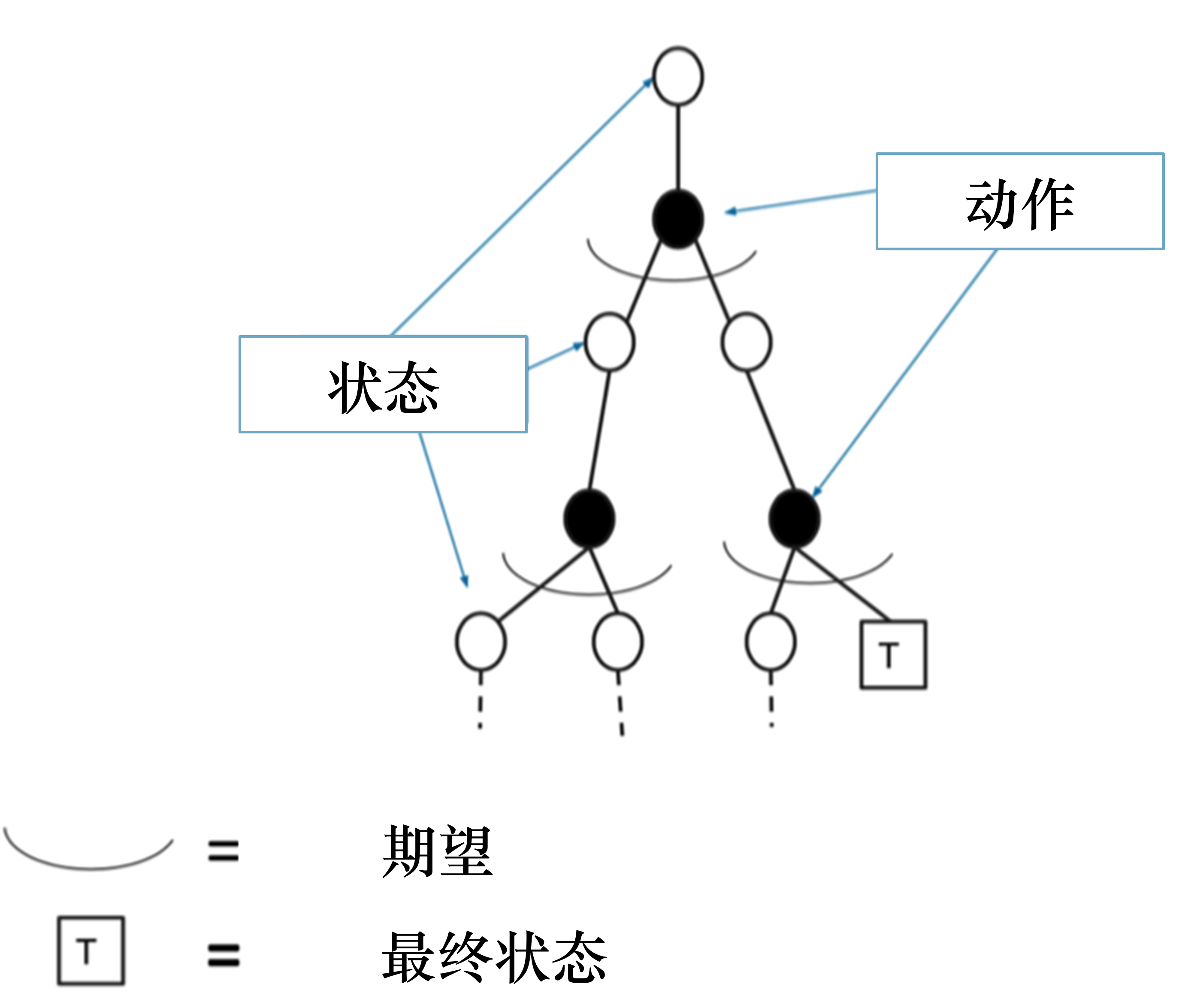
在马尔可夫决策过程中，状态的价值是其期望回报；利用蒙特卡洛方法在 MDP 上采样许多条序列，计算每个序列的真实回报，公式如下：

\[ V_\pi(s)=\mathbb{E}_\pi[G_t|S_t=s]=\frac{1}{N}\sum_{i=1}^{N}G_t^{(i)} \]

在一条序列中，在某个状态每一次出现时计算它的回报。假设当前使用策略\(\pi\)从状态\(s\)开始采样序列，为每一个状态维护一个计数器和总回报，计算状态价值函数的具体过程如下（经验均值）：

  1. 使用策略\(\pi\)采样若干条序列： \[ s_0^{(i)}\rightarrow r_0^{(i)}, s_1^{(i)}\rightarrow r_1^{(i)},...,s_{T-1}^{(i)}\rightarrow r_{T-1}^{(i)} \]

  2. 对每一条序列中的每一时间\(t\)的状态\(s\)进行如下操作：

    • 更新状态\(s\)的计数器：\(N(s)\leftarrow N(s)+1\)；
    • 更新状态\(s\)的总回报：\(M(s)\leftarrow M(s)+G(t)\).

  3. 每一个状态的价值被估计为回报的平均值：\(V(s)=\frac{M(s)}{N(s)}\)

根据大数定律，当\(N(s)\rightarrow\infty\)时，有\(V(s)\rightarrow V_\pi(s)\).

也可以计算增量均值：

  • \(N(s)\leftarrow N(s)+1\)；
  • \(V(s)\leftarrow V(s)+\frac{1}{N(s)}(G-V(s))\)

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
def sample(MDP, Pi, timestep_max, number):
    ''' 采样函数,策略Pi,限制最长时间步timestep_max,总共采样序列数number '''
    S, A, P, R, gamma = MDP
    episodes = []
    for _ in range(number):
        episode = []
        timestep = 0
        s = S[np.random.randint(4)]  # 随机选择一个除s5以外的状态s作为起点
        # 当前状态为终止状态或者时间步太长时,一次采样结束
        while s != "s5" and timestep <= timestep_max:
            timestep += 1
            rand, temp = np.random.rand(), 0
            # 在状态s下根据策略选择动作
            for a_opt in A:
                temp += Pi.get(join(s, a_opt), 0)
                if temp > rand:
                    a = a_opt
                    r = R.get(join(s, a), 0)
                    break
            rand, temp = np.random.rand(), 0
            # 根据状态转移概率得到下一个状态s_next
            for s_opt in S:
                temp += P.get(join(join(s, a), s_opt), 0)
                if temp > rand:
                    s_next = s_opt
                    break
            episode.append((s, a, r, s_next))  # 把（s,a,r,s_next）元组放入序列中
            s = s_next  # s_next变成当前状态,开始接下来的循环
        episodes.append(episode)
    return episodes

# 对所有采样序列计算所有状态的价值
def MC(episodes, V, N, gamma):
    for episode in episodes:
        G = 0
        for i in range(len(episode) - 1, -1, -1):  #一个序列从后往前计算
            (s, a, r, s_next) = episode[i]
            G = r + gamma * G
            N[s] = N[s] + 1
            V[s] = V[s] + (G - V[s]) / N[s] # 增量更新


timestep_max = 20
# 采样1000次
episodes = sample(MDP, Pi_1, timestep_max, 1000)
gamma = 0.5
V = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
N = {"s1": 0, "s2": 0, "s3": 0, "s4": 0, "s5": 0}
MC(episodes, V, N, gamma)
print("使用蒙特卡洛方法计算MDP的状态价值为\n", V)

对于同一个 MDP，不同策略访问到的状态的概率分布不同，因此不同策略的价值函数不同。

定义 MDP 的初始状态分布为\(\nu_0(s)\)，采用\(P_t^{\pi}(s)\)表示采取策略\(\pi\)使得智能体在\(t\)时刻状态为\(s\)的概率（有\(P_0^{\pi}(s)=\nu_0(s)\)），定义策略\(\pi\)的状态访问分布为：

\[ \nu^{\pi}(s)=(1-\gamma)\sum_{t=0}^{\infty}\gamma^t P_t^\pi(s) \]

其中，\(1-\gamma\)是使得概率和为1的归一化因子。有：

\[ \nu^{\pi}(s')=(1-\gamma)\nu_0(s')+\gamma\int P(s'|s,a)\pi(a|s)\nu^{\pi}(s)dsda \]

策略\(\pi\)的占用度量：表示动作状态对\((s,a)\)被访问到的概率：

\[ \rho^{\pi}(s,a)=\nu^{\pi}(s)\pi(a|s) \]

两个定理：

定理1（判断策略是否相同）：智能体分别以策略\(\pi_1\)和\(\pi_2\)和同一个 MDP 交互得到的占用度量\(\rho^{\pi_1}\)和\(\rho^{\pi_2}\)满足：

\[ \rho^{\pi_1}=\rho^{\pi_2}\Longleftrightarrow \pi_1=\pi_2 \]

定理2：给定一合法占用度量\(\rho\)，可生成该占用度量的唯一策略是：

\[ \pi_\rho=\frac{\rho(s,a)}{\sum_{a'}\rho(s,a')} \]

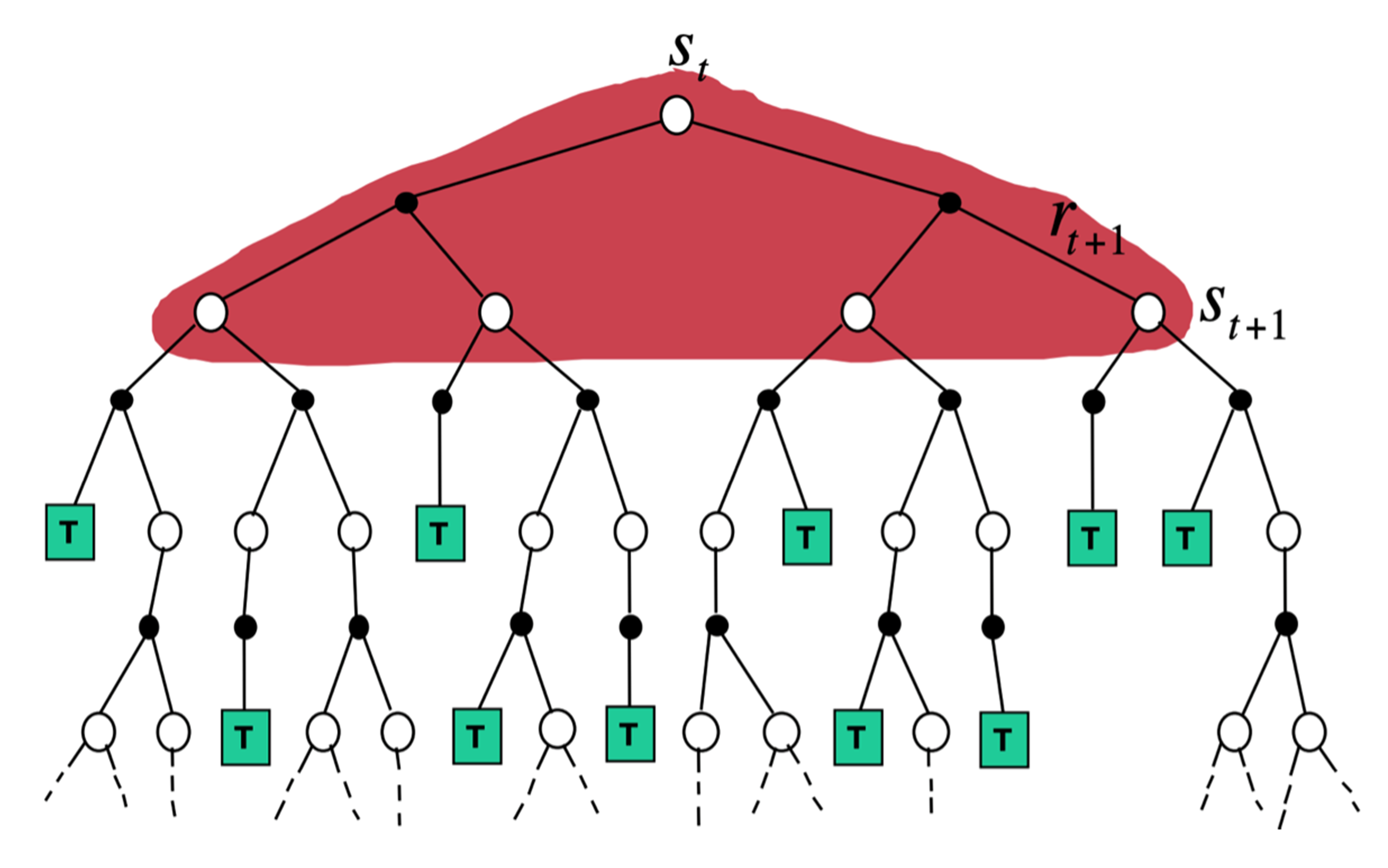
占用度量的近似估计：设置一个较大的采样轨迹长度的最大值，采样很多次，用状态动作对出现的频率估计实际概率。

对比蒙特卡洛与动态规划

动态规划采用自举（基于之前估计的量来估计一个量），通过上一个时刻的\(V_{i-1}(s)\)更新当前时刻的\(V_i(s)\)，即：

\[ V_i(s)\leftarrow \sum_{a\in A}\pi(a|s)(R(s,a)+\gamma\sum_{s'\in S}P(s'|s,a)V_{i-1}(s')) \]

贝尔曼期望备份有两层加和，计算两次期望，得到一个更新。

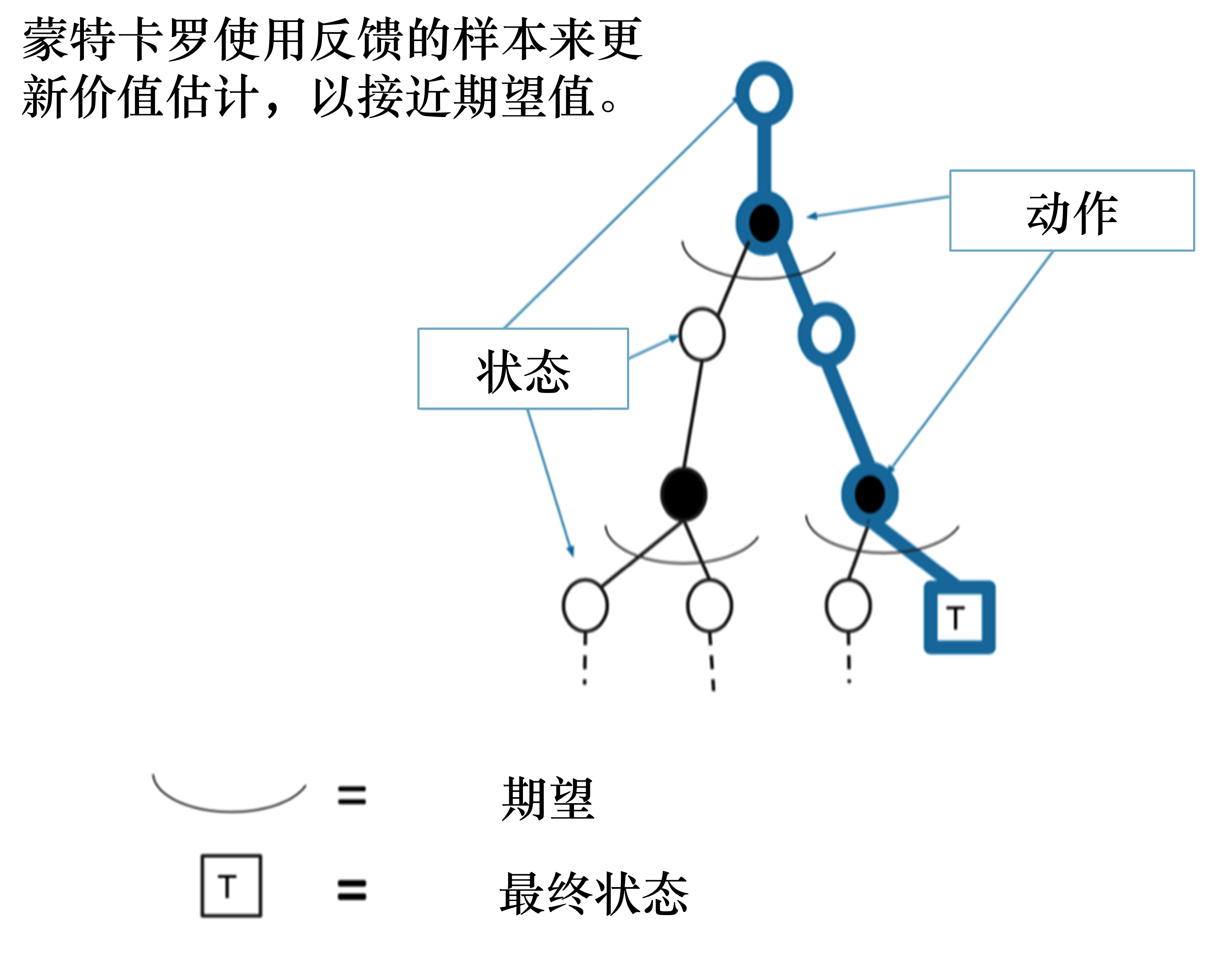
蒙特卡洛通过多条轨迹序列的平均回报（真实奖励）进行更新，即：

\[ V(s_t)\leftarrow V(s_t)+\alpha(G_{i,t}-V(s_t)) \]

轨迹上的状态和采取的动作均已生成：只更新这条轨迹上的所有状态。

动态规划适用于有模型学习（已知状态价值函数和奖励函数），蒙特卡洛适用于免模型学习；蒙特卡洛方法只需要更新一条轨迹的状态，动态规划方法需要更新所有的状态。

状态数量较多时，采用动态规划迭代速度慢；采用蒙特卡洛方法更合适。

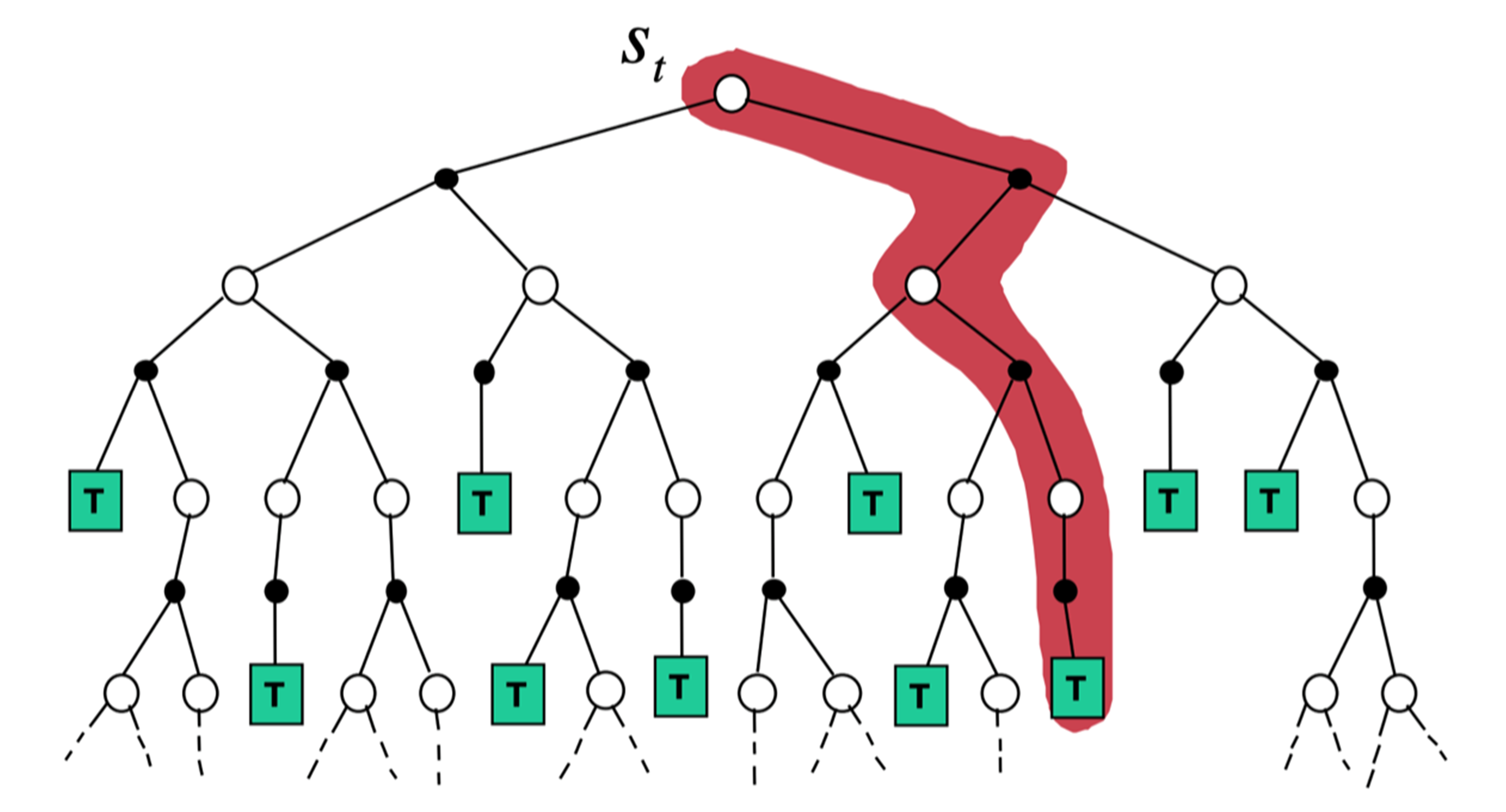
时序差分方法

时序差分的思想：在不断的重复实验后，下一个状态的价值可以不断地强化影响上一个状态的价值。

对比蒙特卡洛的增量更新方式：

\[ V(s_t)\leftarrow V(s_t)+\alpha[G_t-V(s_t)] \]

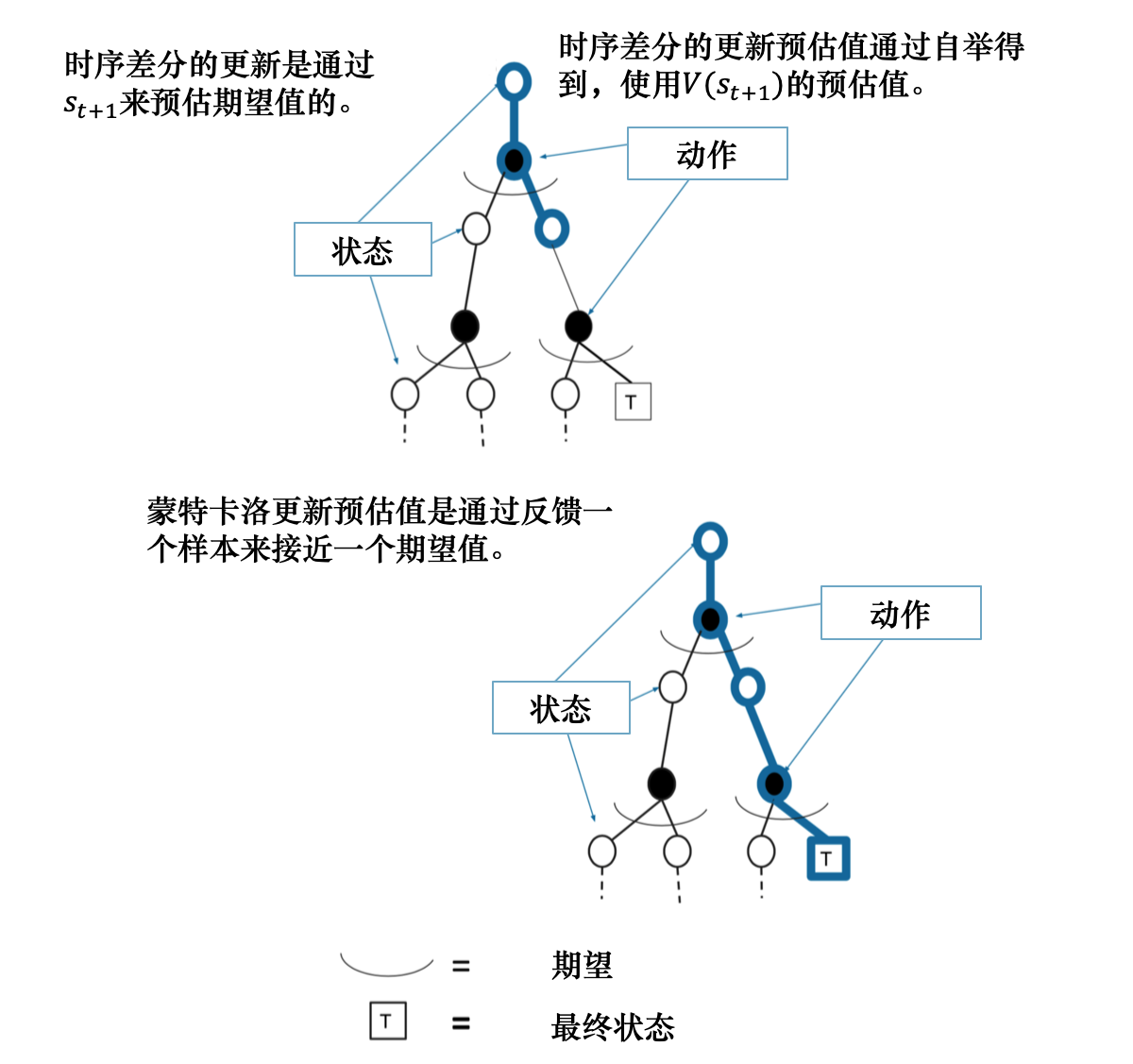
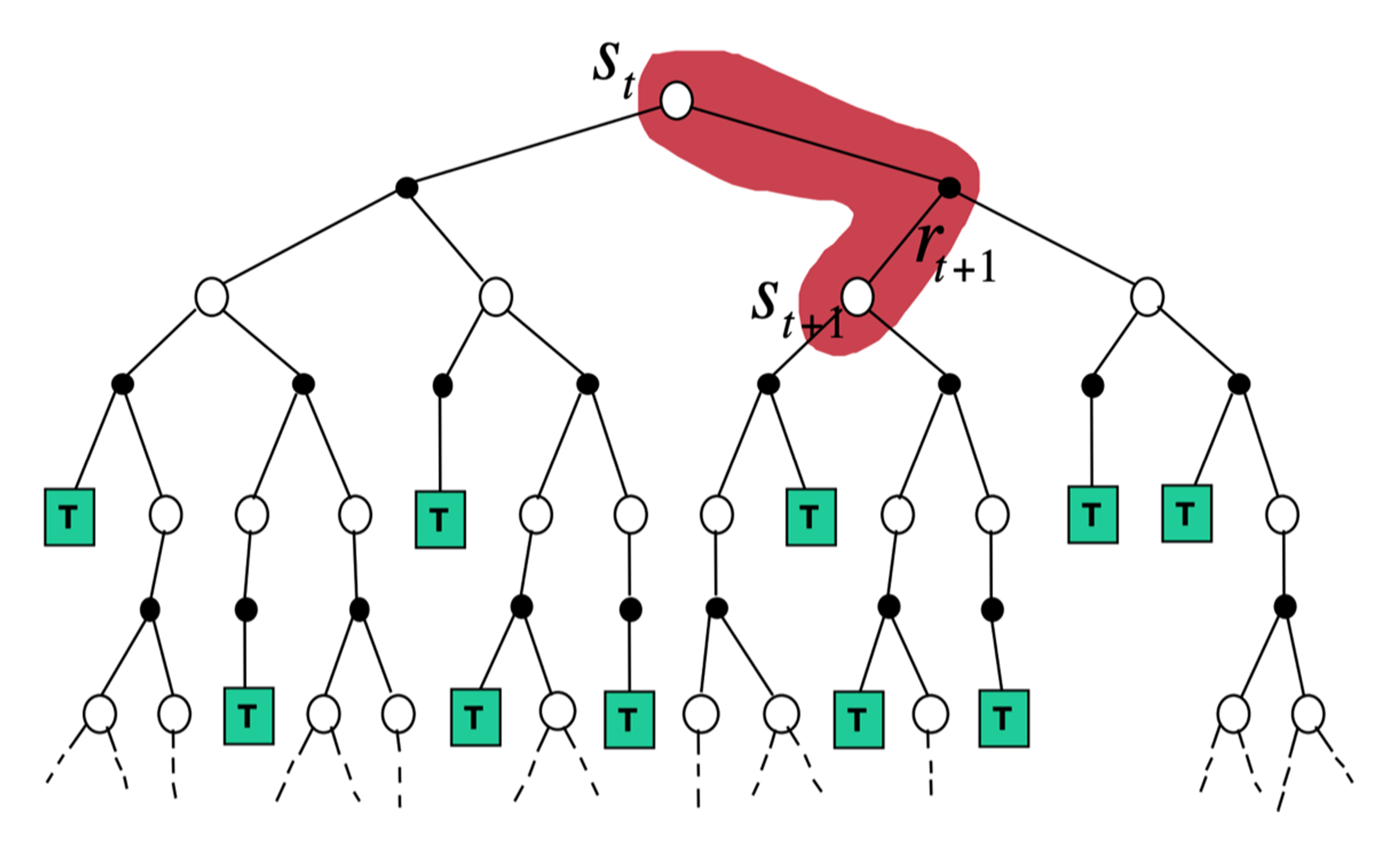
蒙特卡洛必须等到整个序列结束之后才能计算回报\(G_t\)；时序差分对于给定策略\(\pi\)，在线（online）地计算其价值函数\(V_\pi\)（一步一步算），对于一步时序差分（TD(0)），每往前走一步就做一次自举，即当前步结束即可更新上一时刻的值\(V(s_t)\)：

\[ V(s_t)\leftarrow V(s_t)+\alpha(r_{t+1}+\gamma V(s_{t+1})-V(s_t)) \]

时序差分误差：\(r_{t+1}+\gamma V(s_{t+1})-V(s_t)\).

可以使用\(r_{t+1}+\gamma V(s_{t+1})\)代替\(G_t\)以更新\(V_\pi(s)\)的原因是：

\[ \begin{align*} V_\pi(s)&=\mathbb{E}_\pi[G_t|s_t=s] \\ &=\mathbb{E}_\pi[\sum_{k=0}^\infty\gamma^k r_{t+k+1}|s_t=s] \\ &=\mathbb{E}_\pi[r_{t+1}+\gamma\sum_{k=0}^\infty\gamma^{k} r_{t+k+2}|s_t=s] \\ &=\mathbb{E}_\pi[r_{t+1}+\gamma V_\pi(s_{t+1})|s_t=s] \\ \end{align*} \]

蒙特卡洛方法采用第一行更新；时序差分方法采用最后一行更新。

\(n\)步时序差分为：

\[ G_t^n=r_{t+1}+\gamma r_{t+2}+...+\gamma^{n-1}r_{t+n}+\gamma^n V(s_{t+n}) \]

使用\(G_t^n\)更新\(V(s_t)\)：

\[ V(s_t)\leftarrow V(s_t)+\alpha(G_t^n-V(s_t)) \]

对比蒙特卡洛和时序差分

  1. 时序差分方法可以在线学习，每走一步就可以更新，效率高；蒙特卡洛方法必须等轨迹结束时才可以学习；

  2. 时序差分方法可以从不完整序列上学习；蒙特卡洛方法只能从完整的序列上进行学习；

  3. 时序差分方法可以在连续的环境下（没有终止）进行学习；蒙特卡洛方法只能在有终止的情况下学习。

三者对比：动态规划方法、蒙特卡洛方法以及时序差分方法的自举和采样

自举：更新时使用了估计。蒙特卡洛方法没有使用自举；动态规划方法和时序差分方法使用了自举。

采样：更新时通过采样得到一个期望。蒙特卡洛方法是纯采样方法；动态规划方法没有使用采样，直接使用贝尔曼期望方程更新状态价值；时序差分方法使用采样，其目标由两部分组成，一部分是采样，一部分是自举。

  1. 动态规划：直接计算期望，将所有相关状态加和，即： \[ V(s_t)\leftarrow\mathbb{E}_{\pi}[r_{t+1}+\gamma V(s_{t+1})] \]

  2. 蒙特卡洛：在当前状态下，生成一条轨迹，在当前轨迹上进行更新，即： \[ V(s_t)\leftarrow V(s_t)+\alpha(G_t-V(s_t)) \]

  3. 时序差分：从当前状态开始，往前走了一步，即： \[ TD(0)=V(s_t)\leftarrow V(s_t)+\alpha(r_{t+1}+\gamma V(s_{t+1})-V(s_t)) \]

  • 时序差分扩展广度，转化为动态规划（考虑所有状态）；
  • 时序差分扩展深度，转化为蒙特卡洛（采样结束到达中止状态）。

Sarsa: on-policy 时序差分

回到策略迭代的步骤：策略评估+策略提升。

  1. 策略评估：计算一个策略的状态价值函数（可通过动态规划/蒙特卡洛/时序差分等方式计算）；
  2. 策略提升：贪心地在每一个状态选择\(Q\)最大的动作，更新策略\(\pi\)；但是当我们不知道奖励函数和状态转移时，如何进行策略的优化？（关键是估计\(Q\)函数）

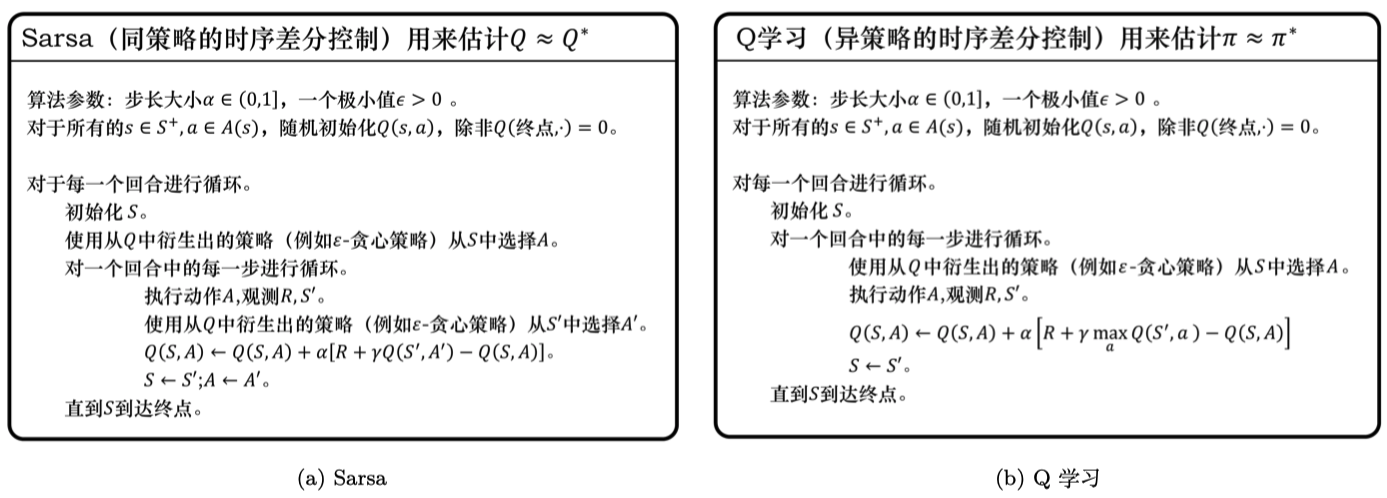
Sarsa 算法直接使用时序差分估计\(Q\)：

\[ Q(s_t, a_t)\leftarrow Q(s_t, a_t)+\alpha[r_{t+1}+\gamma Q(s_{t+1}, a_{t+1})-Q(s_t, a_t)] \]

对于单步 Sarsa，每执行一个动作，就会更新一次价值和策略。

对于\(n\)步 Sarsa，其\(Q\)回报为：

\[ Q_t^n=r_{t+1}+\gamma r_{t+2}+...+\gamma^{n-1}r_{t+n}+\gamma^n Q(s_{t+n}, a_{t+n}) \]

给\(Q_t^n\)加上资格迹衰减参数\(\lambda\)并求和，可得到 Sarsa(\(\lambda\))的\(Q\)回报：

\[ Q_t^{\lambda}=(1-\lambda)\sum_{n=1}^{\infty}\lambda^{n-1}Q_t^n \]

\(n\)步 Sarsa(\(\lambda\))的更新策略为：

\[ Q(s_t, a_t)\leftarrow Q(s_t, a_t)+\alpha(Q_t^\lambda-Q(s_t, a_t)) \]

Sarsa 和 Sarsa(\(\lambda\))的差别主要是价值的更新。

Q-learning: off-policy 时序差分

更新方式为：

\[ Q(s_t, a_t)\leftarrow Q(s_t, a_t)+\alpha[r_{t+1}+\gamma\max_a Q(s_{t+1}, a)-Q(s_t, a_t)] \]

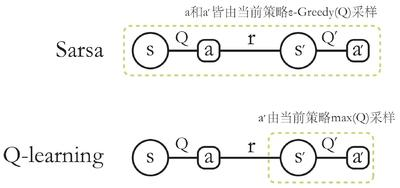
Q-learning 和 Sarsa 的更新公式相同，区别在于目标计算：Sarsa 是\(r_{t+1}+\gamma Q(s_{t+1}, a_{t+1})\)，Q-learning 是\(r_{t+1}+\gamma\max_a Q(s_{t+1}, a)\).

概念：采样数据的策略称为行为策略，利用这些数据来更新的策略称为目标策略。

on-policy && off-policy：行为策略和目标策略相同即为 on-policy；反之为 off-policy。在这里，区别在于：计算时序差分的价值目标的数据是否来自当前的策略。

  • Sarsa：更新公式来自当前策略采样得到的\((s,a,r,s',a')\)，是 on-policy 策略；
  • Q-learning：更新公式使用\((s,a,r,s')\)以更新当前状态动作对的价值\(Q(s,a)\)，是 off-policy 策略。

区别在于：Sarsa 使用\(a'\)更新Q表格（\(a'\)是下一个步骤一定执行的动作）；Q-learning 使用\(Q(s',a)\)最大值对应的动作（不一定是下一个步骤执行的动作）。即：Q-learning 无需传入\(a'\).