RL 系列:1. Markov 决策过程
本文旨在阐述基于 Markov 决策过程的强化学习原理,聚焦于关键公式(省去一些繁杂的数学推导),快速领会 RL 的核心理念。
RL 概述
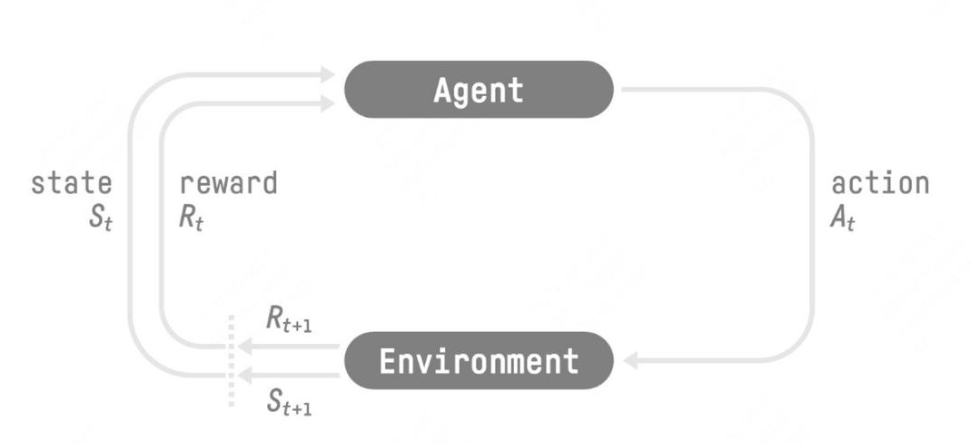
强化学习的理念:Agent 根据 Environment 输出的 \(S_t\) 和 \(R_t\) 综合判断,产生当前步骤的动作 \(A_t\),放入 Environment 执行;Environment 根据 \(A_t\) 执行的结果,输出下一个状态 \(S_{t+1}\) 和当前动作带来的奖励 \(R_{t+1}\),返回给 Agent。
强化学习和监督学习的区别:
- RL 得到的时序数据不满足独立同分布;
- RL 无实时明确反馈当前 Action 是否正确,奖励信号延迟。(通过 rollout 过程从当前帧对 Action 进行采样,得到多个 observation, 每个 observe 对应一条 trajectory,即一个 State 和 Action 的序列 τ=(s0,a0,s1,a1,…);通过最终 reward 来观测当前 trajectory 是否合适)
Markov 奖励过程
状态价值函数:\(V^t(s)\)
定义:在状态\(s\)的回报期望 定义: \[ \begin{align*} V^t(s) &= \mathbb{E}[G_t|s_t=s] \\ &= \mathbb{E}[{r_{t+1}+\gamma r_{t+2}+{\gamma}^2 r_{t+3}+...+\gamma^{T-t-1} r_T |s_t=s}] \\ \end{align*} \] 其中,\(T\)是最终时刻,\(\gamma\)是折扣因子。
为什么要加入折扣因子\(\gamma\)呢?
- 部分 Markov 过程带环,我们不希望获得无穷的奖励;
- 由于未来的不确定性,对未来的评估增加一个折扣;
- 更倾向于得到实时奖励(现在的钱比未来的钱更有价值)。
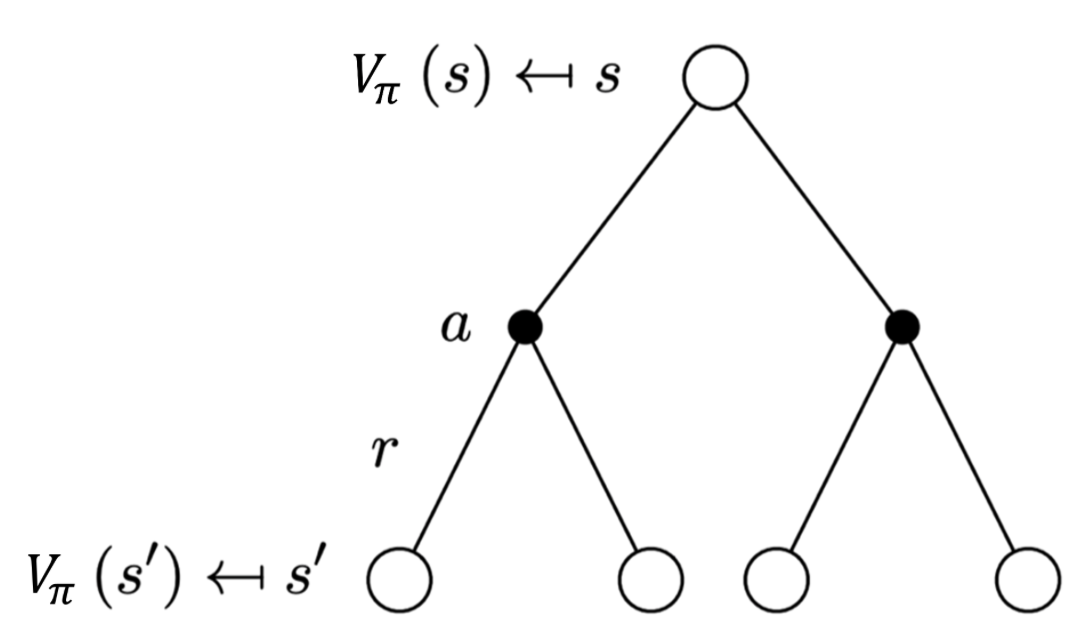
价值函数的贝尔曼方程:当前状态与未来状态之间的迭代关系
表示当前状态的价值函数可以通过下个状态的价值函数来计算。 \[ V(s)=R(s)+\gamma\sum_{s'\in S}p(s'|s)V(s') \]
- \(s'\)代表未来的所有状态;\(p(s'|s)\)是从当前状态转移到未来状态的概率;
- \(V(s), V(s')\)分别对应当前、未来状态的价值。
- \(R(s)\)为即时奖励。
其矩阵形式为:\(V=R+\gamma PV\).
求方程\(V=R+\gamma PV\)的解析解:
\[ \begin{align*} IV=R+\gamma PV \\ (I-\gamma P)V=R \\ V=(I-\gamma P)^{-1}R \\ \end{align*} \] 矩阵求逆过程的复杂度为\(O(N^3)\)。当状态数量极大时,对大矩阵求逆非常困难,因此通过解析解求解只适用于状态数量很小的马尔可夫奖励过程。
两种计算方法:
蒙特卡洛采样:从某个状态开始,把小船放到状态转移矩阵里面,让它“随波逐流”,产生多条轨迹;分别计算每条轨迹对应的回报,累积后取平均值,得到某个状态的价值。
动态规划(基于贝尔曼方程):通过自举不断迭代贝尔曼方程,直到价值函数收敛。
Markov 决策过程
策略函数: \[ \pi(a|s)=p(a_t=a|s_t=s) \]
动作价值函数(Q函数):在状态\(s\)采取动作\(a\),得到的回报期望。 \[ \begin{align*} Q_{\pi}(s, a) &= \mathbb{E}_{\pi}[G_t|s_t=s, a_t=a] \\ &= R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V(s') \\ \end{align*} \]
价值函数\(V_\pi(s)\):对Q函数中的动作进行加和。 \[ \begin{align*} V_\pi(s) &= \mathbb{E}_\pi[G_t|s_t=s] \\ &= \sum_{a\in A}\pi(a|s)Q_\pi(s, a) \\ \end{align*} \]
贝尔曼期望方程
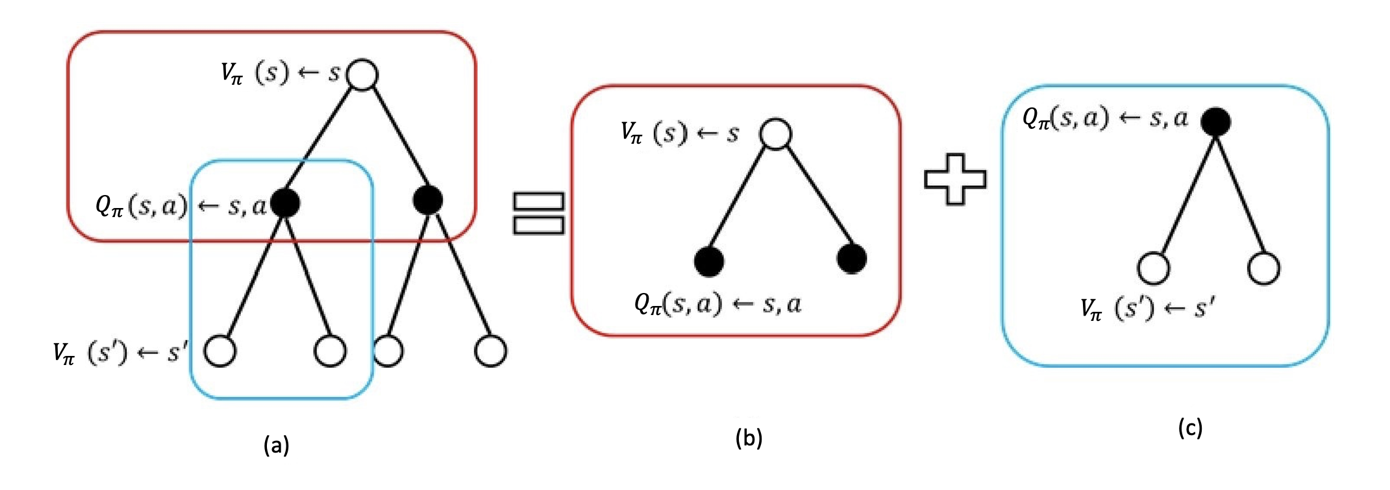
备份图:每一个空心圆圈代表一个状态:每一个实心圆圈代表一个状态-动作对。
- 当前价值与未来价值的关联:(代入\(Q_{\pi}(s, a)\))
\[ V_\pi(s)=\sum_{a\in A}\pi(a|s)(R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V(s')) \]
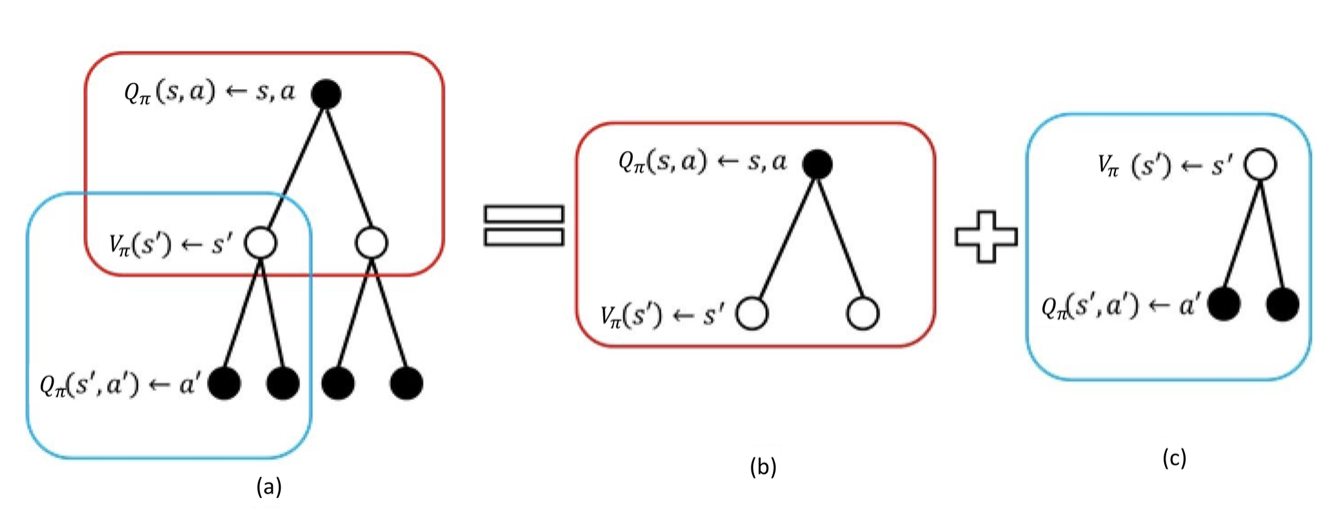
- 当前时刻的Q函数与未来时刻的Q函数之间的关联:(代入\(V_\pi(s')\))
\[ Q_\pi(s, a)=R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)\sum_{a'\in A}\pi(a'|s')Q_\pi(s', a') \]
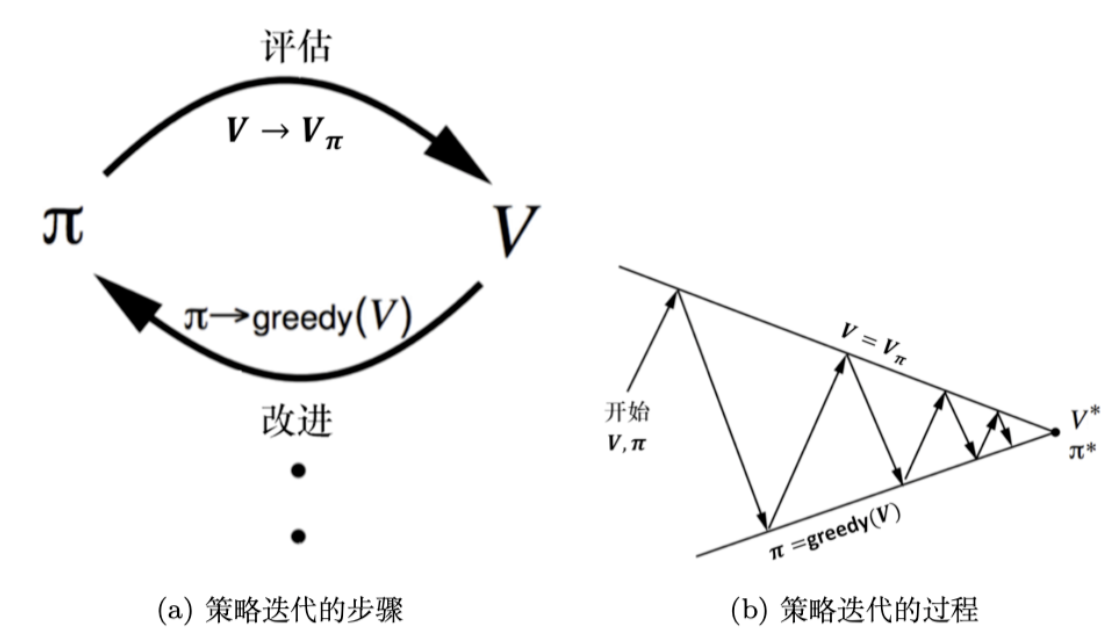
策略迭代=策略评估+策略提升
- 策略评估:给定当前的策略函数\(\pi\),估计状态价值函数\(V\);
- 策略改进:由\(V\)计算\(Q\)函数,最大化Q函数;通过在 Q 函数做一个贪心的搜索来进一步改进策略\(\pi\)。
策略评估
策略评估用于计算一个策略的状态价值函数。从贝尔曼期望方程出发:
\[ V_\pi(s)=\sum_{a\in A}\pi(a|s)(R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V(s')) \]
其中\(\pi(a|s)\)是策略\(\pi\)在状态\(s\)下采取动作\(a\)的概率。根据动态规划的思想,将计算下一个可能状态的价值作为子问题,计算当前状态的价值作为当前问题。更一般地,考虑所有的状态,问题转化为:利用上一轮的状态价值函数计算当前这一轮的状态价值函数,即:
\[ V^{k+1}(s)=\sum_{a\in A}\pi(a|s)(R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V^k(s')) \]
选定任意初始值\(V^0\),\(V^k=V_\pi\)是贝尔曼期望方程的不动点,即\(k\rightarrow\infty\)时,序列\({V^k}\)收敛至\(V_pi\).
在实际实现中,如果某一轮的\(\max_{s\in S}|V^{k+1}(s)-V^{k}(s)|\)的值非常小,即可结束策略评估。
策略提升
使用策略评估得到当前策略\(\pi\)得的状态价值函数\(V_\pi\),即得到策略\(\pi\)下从每一个状态\(s\)出发得到的期望回报。如何优化策略\(\pi\)以实现在状态\(s\)下获得更高的期望回报呢?
假设智能体在状态\(s\)下采取动作\(a\),后续动作遵循策略\(\pi\),此时得到的期望回报是动作价值\(Q_{\pi}(s, a)\);如果有\(Q_{\pi}(s, a)\geq V_\pi(s)\),说明在状态\(s\)下采取动作\(a\)相比原先策略\(\pi(a|s)\)得到更高的期望回报。(这个讨论只针对状态\(s\))
假设存在一个确定性策略\(\pi'\),在任意一个状态\(s\)下,均满足:
\[ Q_\pi(s', \pi'(s))\geq V_\pi(s) \]
那么如何这样的\(\pi'\)呢?贪心地在每一个状态选择动作价值\(Q\)最大的动作,也即: \[ \begin{align*} \pi'(s)&=\argmax_{a}Q_\pi(s, a) \\ &=\argmax_a[R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V_\pi(s')] \end{align*} \]
该过程称为策略提升。当提升后的策略\(\pi'\)和之前的策略\(\pi\)相同时,策略迭代收敛,此时的\(\pi\)是最优策略。
策略迭代算法的过程如下:
\[ \pi^0\overset{\text{策略评估}}{\rightarrow}V_{\pi^0}\overset{\text{策略提升}}{\rightarrow}\pi^1\overset{\text{策略评估}}{\rightarrow}V_{\pi^1}\overset{\text{策略提升}}{\rightarrow}\pi^2 \overset{\text{策略评估}}{\rightarrow}...\overset{\text{策略提升}}{\rightarrow}\pi^* \]
价值迭代
在策略迭代中,策略评估需要执行很多轮才收敛到某一策略的状态价值函数,计算量大,是否一定要等到策略评估完成才能开始策略提升呢?设想一种情况:虽然状态价值函数\(V_\pi\)尚未收敛,但执行策略提升依然能得到同一个最优策略。
一个新的想法为:策略评估只执行一轮价值更新,直接进行策略提升。(这时不存在显式的策略\(\pi\),只维护一个状态价值函数\(V\))
贝尔曼最优方程:当前状态的最佳价值函数值必须等于:在这个状态下采取最好动作得到的回报的期望。
有: \[ \begin{align*} V^*(s)&=\max_a Q^*(s, a) \\ &=\max_a[R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V^*(s')] \end{align*} \]
写成迭代更新的方式为:
\[ V^{k+1}(s)=\max_{a\in A}[R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V^k(s')] \]
当\(V^k\)与\(V^{k+1}\)趋同时,其为贝尔曼最优方程的不动点,此时对应最优状态价值函数\(V^*\);利用\(\pi(s)=\argmax_{a}[R(s, a)+\gamma\sum_{s'\in S}p(s'|s, a)V^{k+1}(s')]\)恢复出最优策略。
策略迭代与价值迭代的区别:
都可以解决 Markov 决策过程的控制问题。
策略迭代:每一次迭代的都包含一个完整策略,中间状态有意义。
价值迭代:对于所有状态,分别迭代价值函数直至收敛,得到最佳价值\(V^*\);类似于价值从某一个状态反向传播到其他各个状态的过程,中间过程的策略和价值函数无意义。得到最优价值后,才提取最佳策略。
总结:策略迭代分两步。首先进行策略评估,即对当前已经搜索到的策略的状态价值函数进行估值;得到估值后,把 Q 函数算出来,更新策略。不断重复这两步,直到策略收敛。价值迭代直接使用贝尔曼最优方程进行迭代,从而寻找最佳的价值函数。找到最佳价值函数后,再提取最佳策略。
小结:使用动态规划算法来解 Markov 决策过程里面的预测和控制,并且采取不同的贝尔曼方程。
对于预测问题(即策略评估的问题),不停地执行贝尔曼期望方程,这样可以估计出给定的策略,然后得到价值函数;
对于控制问题,如果采取策略迭代,使用贝尔曼期望方程;如果采取价值迭代,使用贝尔曼最优方程。