并行训练系列:4. 张量并行(TP)
在 ZeRO 系列中,实现了 parameters, gradients 和 optimizer states 的切分,然而在 FWD/BWD 计算时,使用的依然是完整的模型参数(需要预先通过 All-Gather 收集)。能不能在计算时只使用模型参数的一部分呢?
由此引出张量并行(Tensor Parallelism)。
TP 切分方式
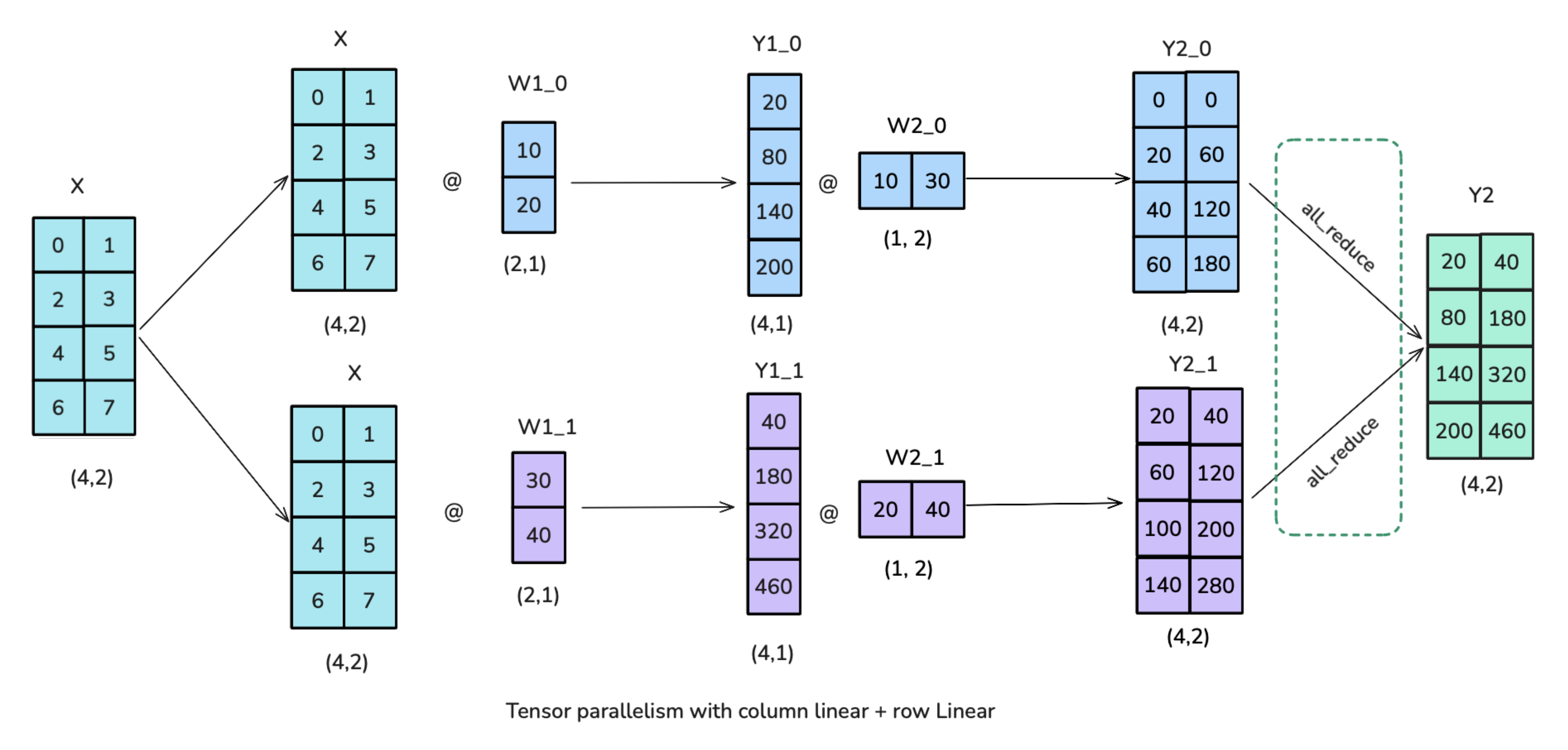
在神经网络中,矩阵乘法常用以下形式表示:\(X\times W\),其中\(X\)为 actication 的输入,\(W\)为模型参数,均以 tensors 的形式保存;tensors 将被沿着一个特定维度切分为 N 个 shards,分布到 N 个 GPU 上。矩阵可以按行或者按列切分,分别对应行并行、列并行。
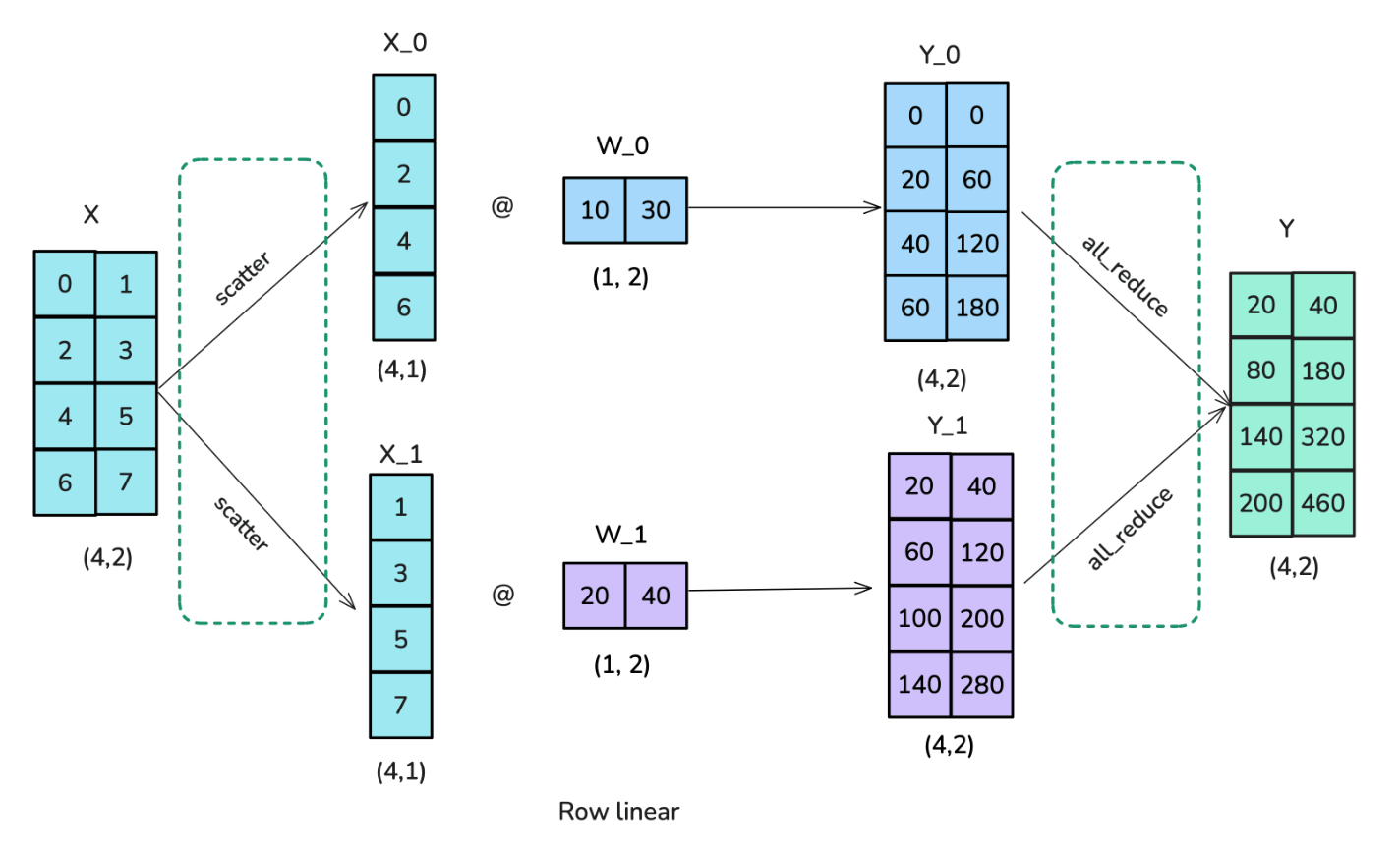
row-linear
forward
- 运用 scatter 操作,将输入矩阵切分为若干个列;
- 将每个权重矩阵切分为若干行,分别与输入矩阵的各列相乘,最后通过 all-reduce 操作相加。
backward
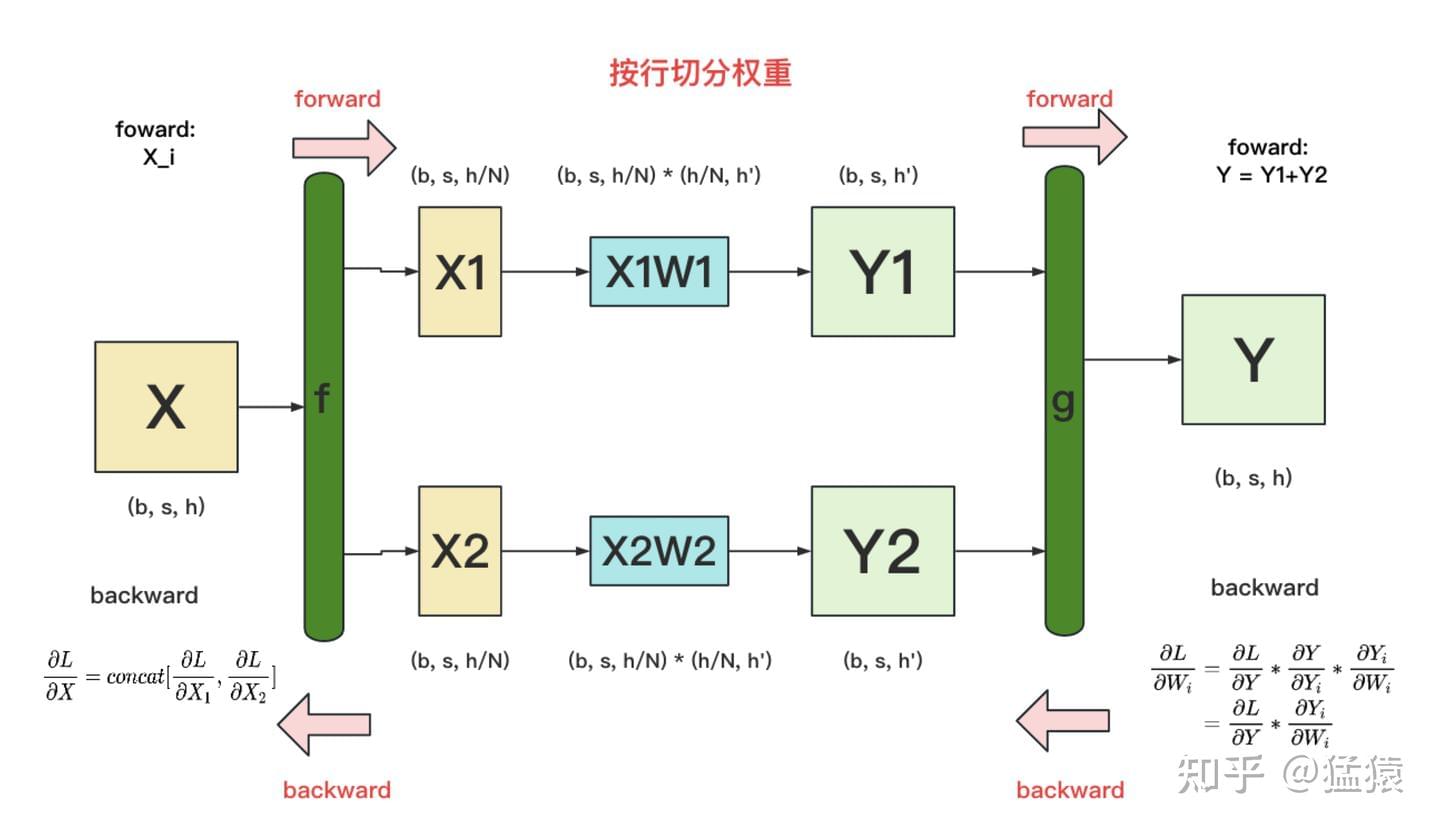
f和g分别表示两个算子(每个算子包含一个 forward+backward 操作)
g的 backward:需要将\(\frac{\partial L}{\partial Y}\)同时广播到两块 GPU 上,就可以独立计算各自权重的梯度\(\frac{\partial L}{\partial W_i}\);f的 backward:注意:上图是一层的计算过程;当模型从上一层向下一层传播时,梯度需要先传播到\(X\),才能往下一层传播(有时间差,可做异步考虑)。
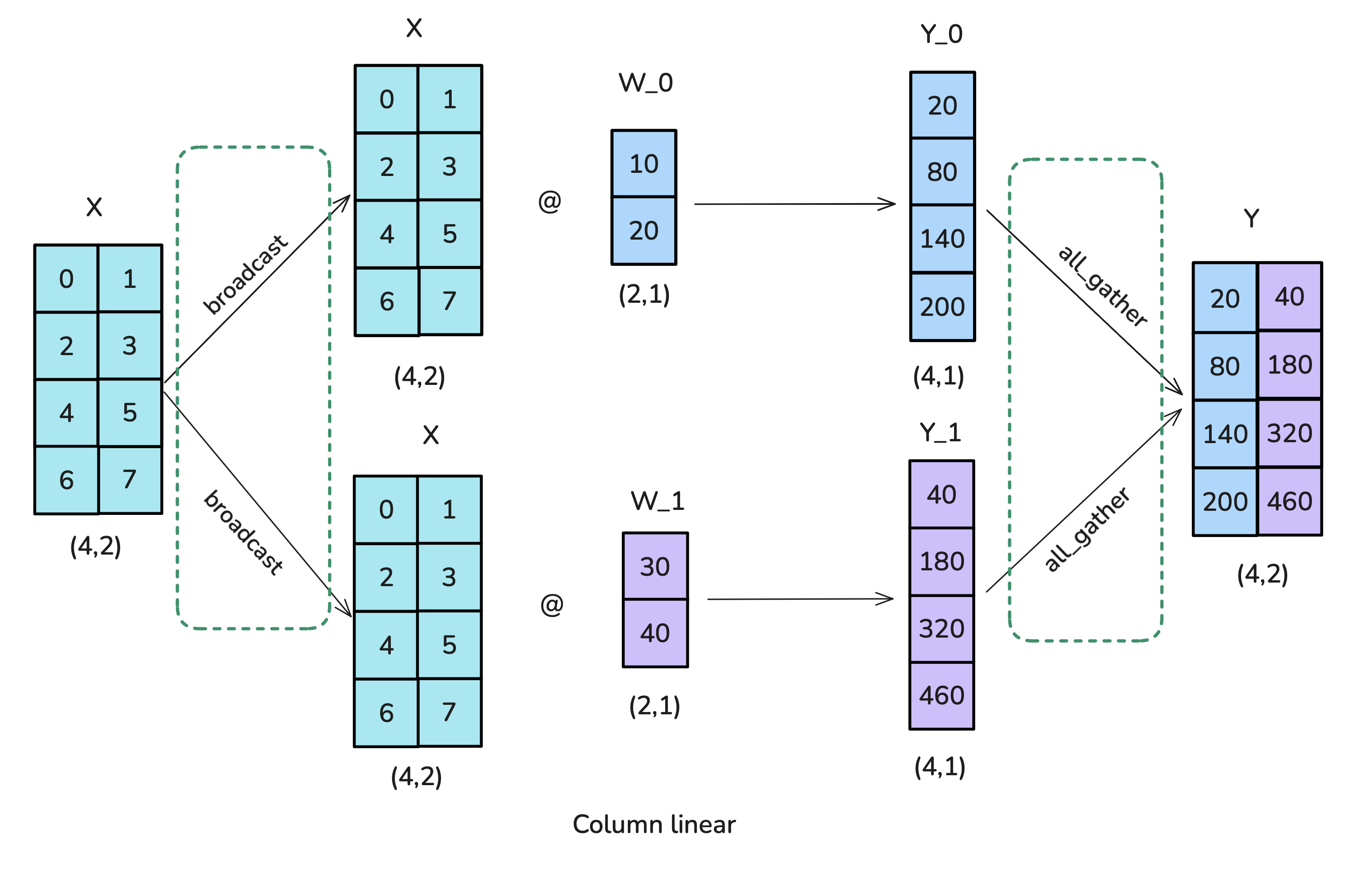
coloumn-linear
forward
- 运用 broadcast 操作,将输入矩阵复制到每个worker;
- 将每个权重矩阵切分为若干个列,分别与输入矩阵相乘,最后通过 all-gather 操作结合。
backward
f的 backward:由于\(X\)同时参加了\(XW_1\)和\(XW_2\)的计算,因此\(\frac{\partial L}{\partial X}=\frac{\partial L}{\partial X}|1+\frac{\partial L}{\partial X}|2\)(其中\(\frac{\partial L}{\partial X}|i\)表示第\(i\)块 GPU 上计算到的\(X\)的梯度。
切分策略
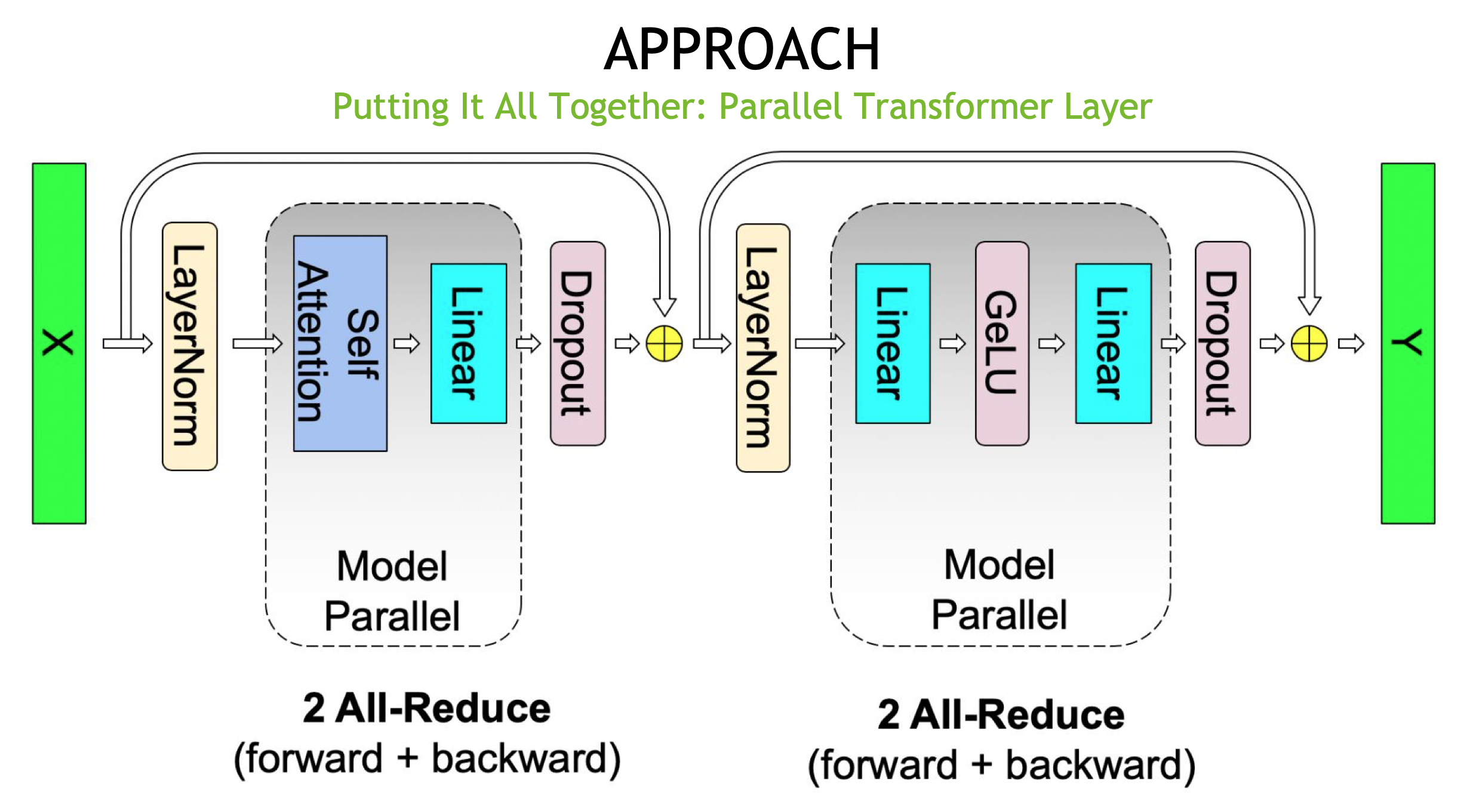
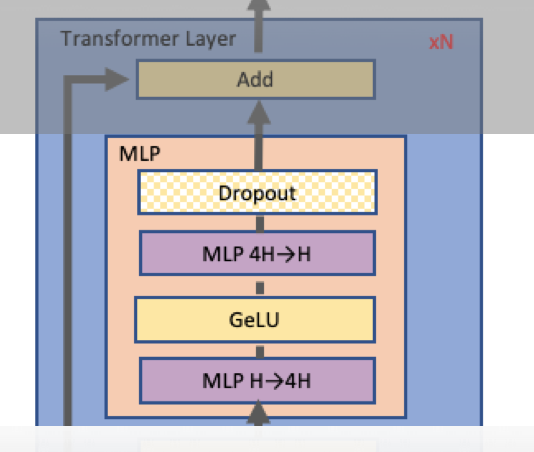
切分 MLP
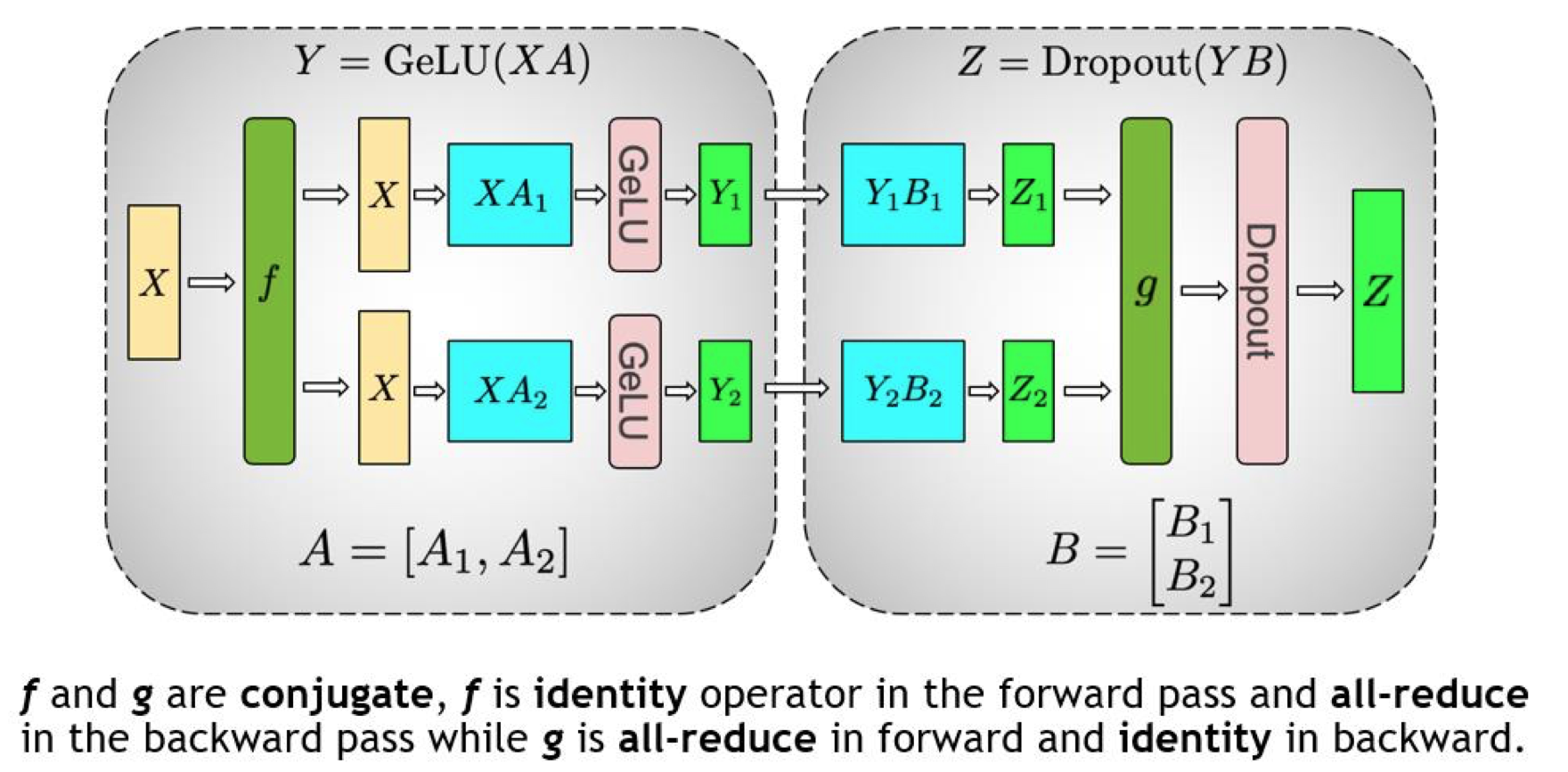
Transformer 层由一个Masked Multi Self Attention和Feed Forward两部分构成,Feed Forward 部分是一个 MLP 网络,由多个全连接层构成,每个全连接层是由矩阵乘操作和GeLU激活层或者 Dropout 构成。 MLP 结构如下:
切分策略如下:
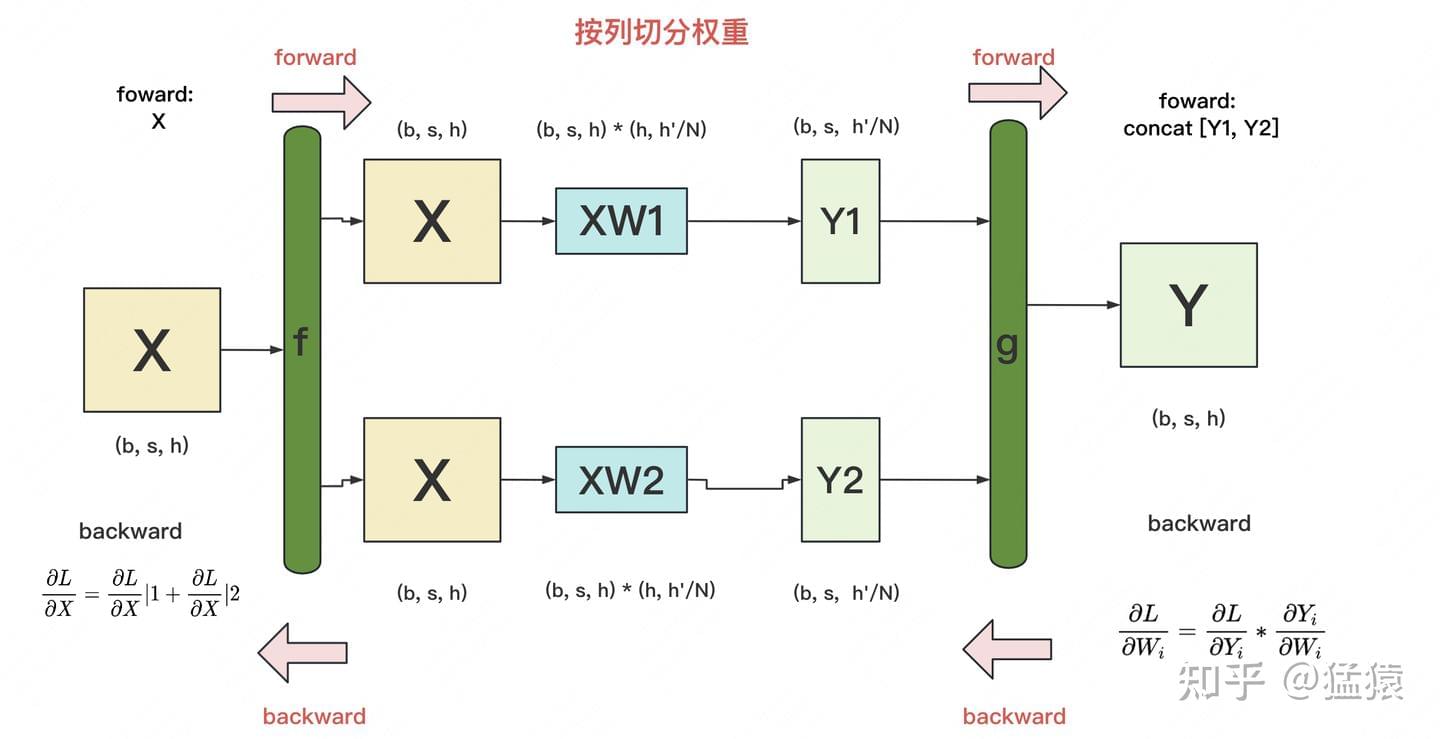
对于第一个全连接层使用 column-linear,第二个全连接层使用row-linear。
看看 Megatron 官方给的完整图:
f的 forward 计算:将输入拷贝到两块 GPU 上,每块独立做 forward 计算;g的 forward 计算:每块 GPU 上的 forward 计算完成,做一次 All-Reduce 获得完整的输出 Z;g的 backward 计算:将\(\frac{\partial L}{\partial Z}\)拷贝到两块 GPU 上,分别独立地做梯度计算;f的 backward 计算:当前层的梯度计算完成、需要传递到下一层时,做一次 All-Reduce 获得完整的梯度\(\frac{\partial L}{\partial X}=\frac{\partial L}{\partial X}|1+\frac{\partial L}{\partial X}|2\)。
为什么要先 column-linear 再 row-linear 呢?看看 Megatron 的官方解释:
如果对权重矩阵\(A\)先做 row-linear,结果:\(Y=GeLU(X_1A_1+X_2A_2)\neq GeLU(X_1A_1)+GeLU(X_2A_2)\)(GeLU 是非线性函数),这样需要再 GeLU 函数之前加一个同步点,增加通信量;
column-linear 操作直接拼接两块 GPU 上的 GeLU 输出,不需要同步点。
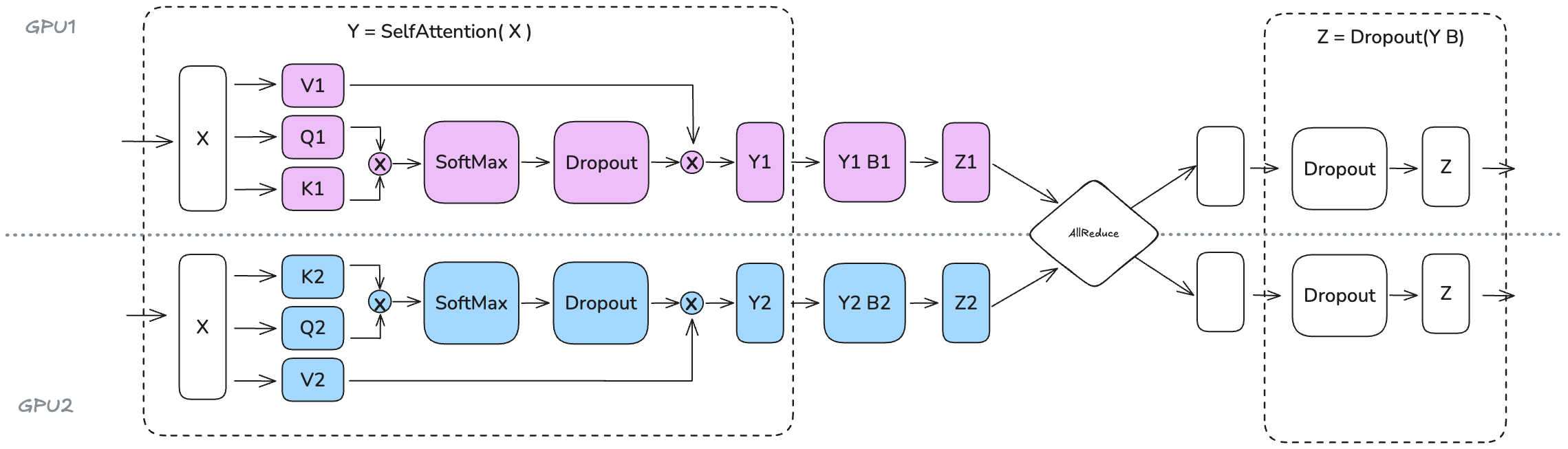
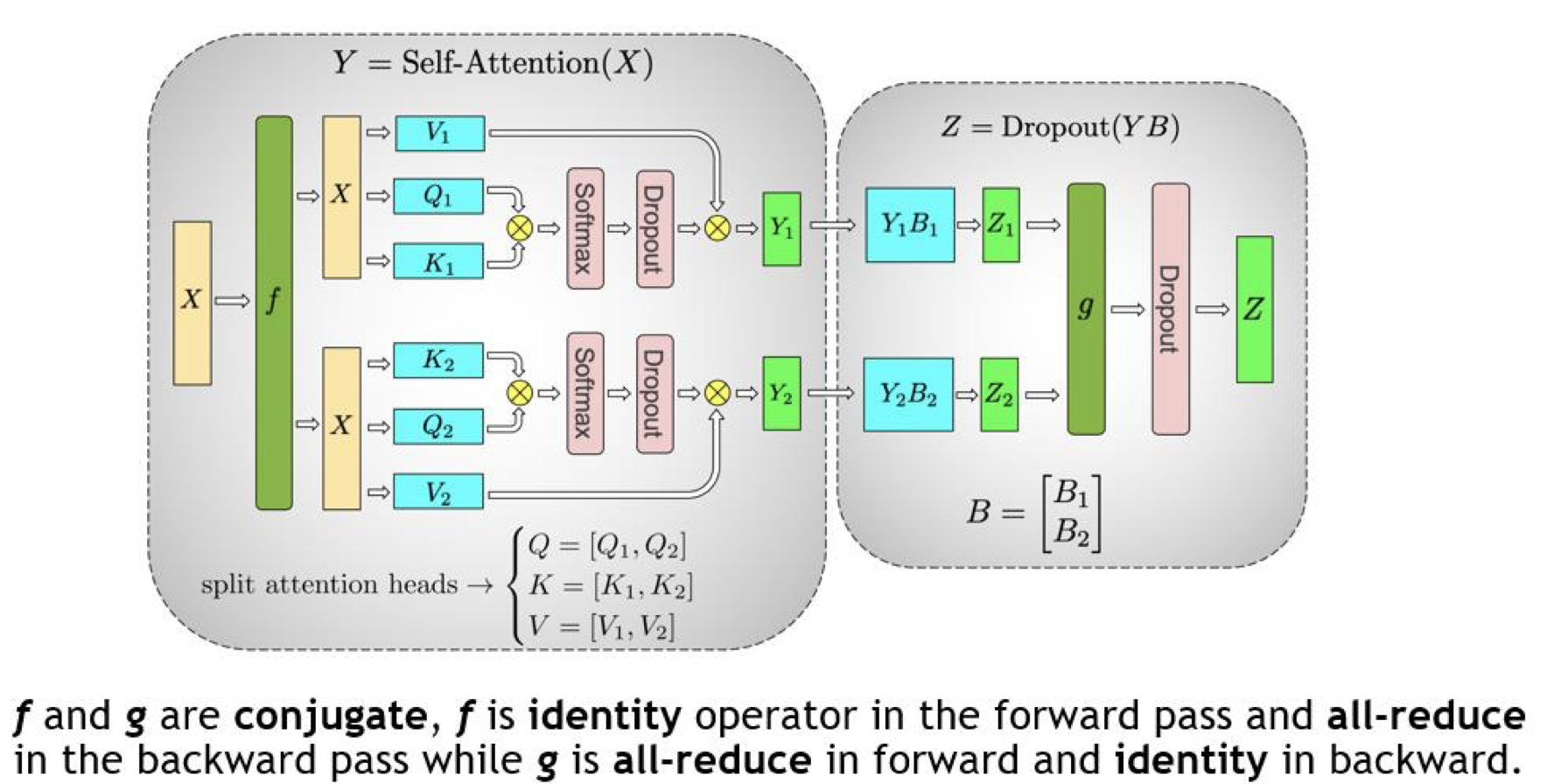
切分 MHA
Attention 模块如下: 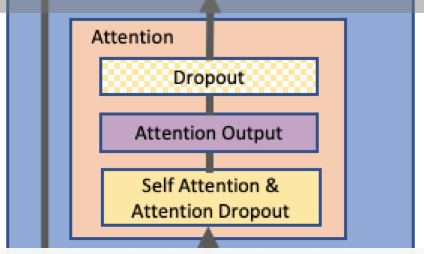
将 Q、K 和 V 矩阵按 column-linear 拆分;输出投影时对权重矩阵按 row-linear 拆分。
看看 Megatron 的图:
对于 Selft-Attention 层:可以利用 MHA 操作中固有的并行性,按列切分:每个 GPU 计算单个/一部分 head 的注意力。(这种方法同样适用于多查询(MQA)或分组查询注意力(GQA),其中,keys 和 values 在 queries 之间共享)
对于全连接层:权重矩阵\(B\)按行切分,与输入\(Y_1, Y_2\)直接计算,通过 All-Reduce 操作和 Dropout 得到最终结果\(Z\)。
值得注意的是,TP degree 不应超过Q/K/V 头的数量,因为需要保证每个 TP rank 上的 head 是完整的(否则无法在每个 GPU 上独立计算注意力,需要额外的通信操作)。
如果使用 GQA,TP 幅度应该实际小于 K/V 头的数量。例如,LLaMA-3 8B 模型有 8 个Key/Value heads,因此TP degree最好不要超过 8;如果我们为这个模型使用 TP=16,那么我们需要在每个 GPU 上复制 K/V 头,并确保它们保持同步。
通信量分析
TP 通信量
MLP 层做 FWD 算子g 一次 All-Reduce;做 BWD 算子 f 一次 All-Reduce。每一次 All-Reduce 通信量为\(2\psi\)(包括一次 Reduce-Scatter 和 All-Gather),总通信量为\(4\psi\),其中:\(\psi=b*s*h\).
MHA 层与 MLP 层类似,总通信量也是\(4\psi\)。
MHA 层和 MLP 层拼接后形成一个 Transformer 模块:
TP 与 DP 通信量对比
刚刚分析了 TP 的通信量:一个 Transformer 层(包含 MLP 层和 MHA 层)的总通信量为\(8\psi=8*b*s*h\).
对于一个朴素 DP,聚合梯度时做一次 All-Reduce 操作,通信量为\(2\psi=2*h*h\)。
TP vs DP 即:\(b*s\) vs \(h\)
实际场景中,前者比后者大,量级一般在\(10^5\)左右。通信量大的最好放在一台机器里(TP);通信量小的可以放在多台机器之间并行(DP)。
参见这个例子:
计算 vs 通信
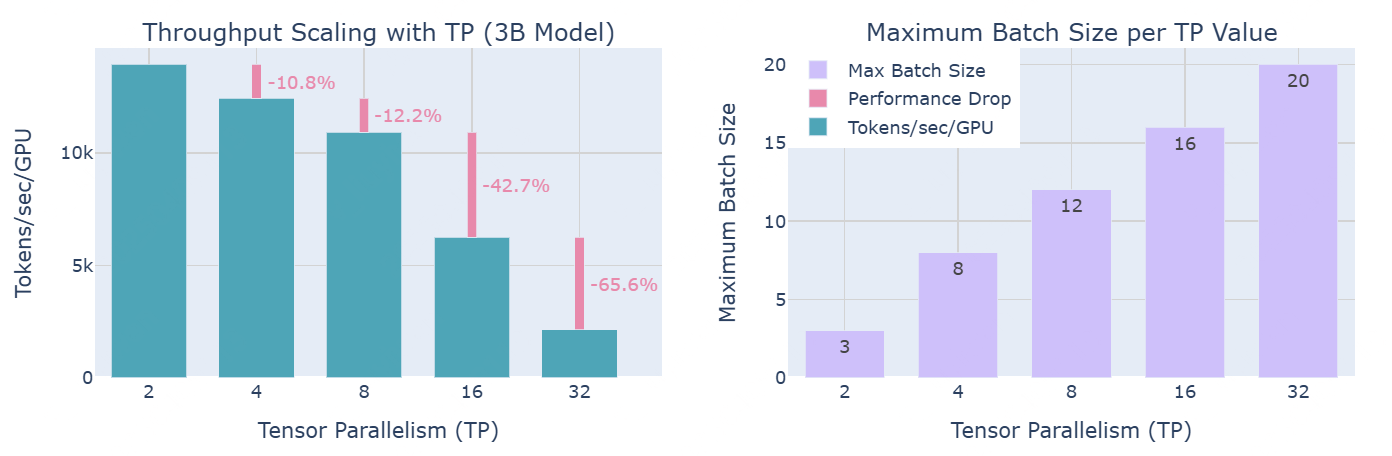
下图展示分布式训练中,计算效率和内存可用性之间的 trade-off :随着TP degree增加,虽然每个GPU的吞吐量减少(左图),但它能够处理更大的批量大小(右图)。
实际上,正如左图所示:TP的通信开销在超越 8 个 GPU 时变得尤为显著:虽然在单节点内使用TP时,可以利用快速的 NVLink 互连,但跨节点通信则依赖于较慢的网络连接;当从 TP=8 增加到 TP=16 时,性能有显著下降;而从 TP=16 增加到 TP=32 时,下降更加明显。在更高的并行度下,通信开销变得如此之高,以至于它迅速主导了计算时间。
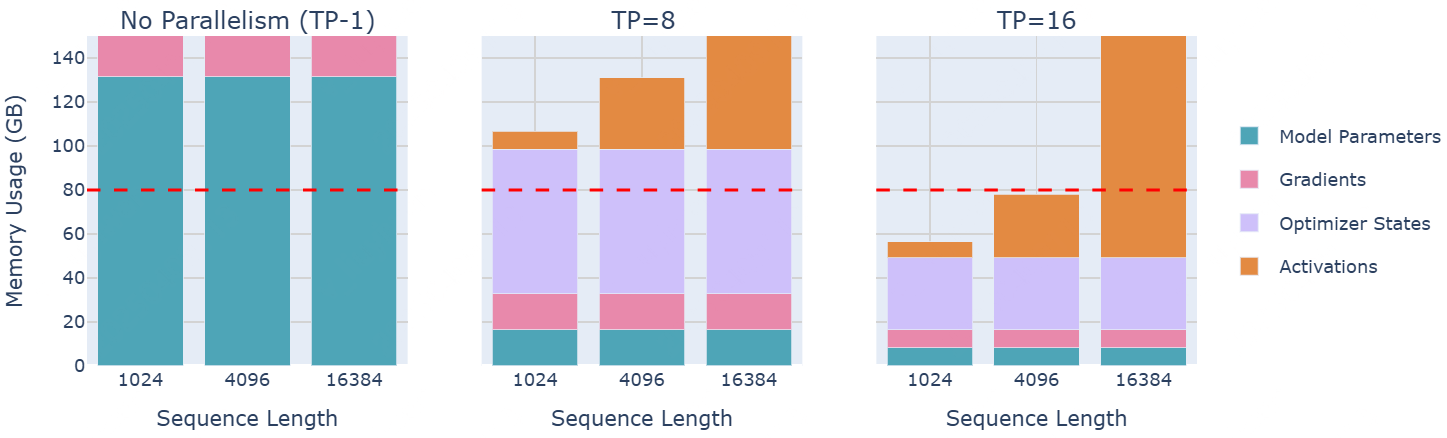
70 B 大模型的显存占用量如下:
是否有办法从 TP 中获得更多的好处呢?可以看到,层归一化(Layer Normalization)和 Dropout 仍然需要在每个 GPU 上收集完整的 activations,这在一定程度上抵消了内存节省。可以通过寻找方法将这些剩余操作也并行化,从而做得更好。
下一篇将 focus on 这个点的优化:序列并行(Sequence Parallelism)。
参考
[源码解析] 模型并行分布式训练Megatron (1) --- 论文 & 基础
图解大模型训练之:张量模型并行(TP),Megatron-LM
MEGATRON-LM: TRAINING BILLION PARAMETER LANGUAGE MODELS WITH GPU MODEL PARALLELISM
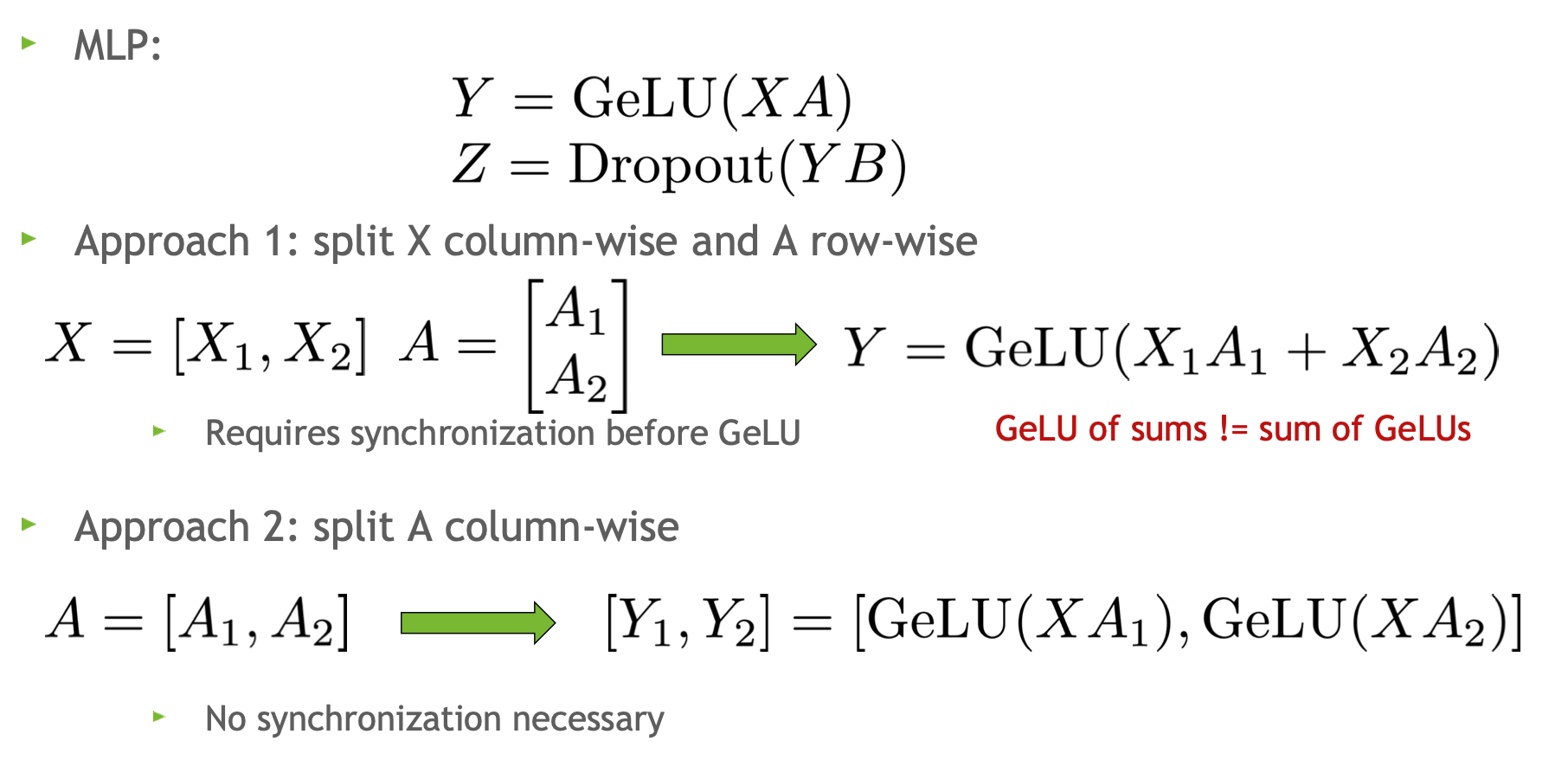 如果对权重矩阵
如果对权重矩阵